地表土壤探测及传感器优化布设

Terrain Soil Sensing and Optimal Deployment of Sensors

摘要: 复杂多变的越野环境对车辆行进的机动性、灵活性具有重要影响，为提高越野车辆机动性必须对地形、坡度、土壤类型、水分、植被等地表土壤属性进行探测。本文首先对最新涌现的探测技术进行分析比较，发现在地表原位布设轻量级的传感器节点可以快速准确全面地监测土壤属性。据此我们提出了土壤传感器节点的优化布设方案，仿真结果表明该方案既保证了监测区域的覆盖率又提高了节点自身的定位精度，具有实际的应用价值。

Abstract: Complex and changeable off-road environment influences the mobility and flexibility of vehicle a lot. To improve mobility of off-road vehicles, the terrain conditions including slops, soil types, moisture content and vegetative cover must be sensed. In this paper, the state-of-the-art sensing techniques are analyzed and compared firstly, the comparison results show that by deploying light weight sensors in situ soil, the soil properties can be monitored quickly and precisely. Based on this, an optimal soil sensor deployment method is proposed. Simulation results show that this method not only guarantees the coverage ratio of sensing area but also improves localization precision of sensors, which possesses practical value of application.

1. 引言

现代战争越发突出机动性的作用，我军提出陆军要由区域防卫型向全域机动性转变，并提高远程机动和快速突击能力 [1] 。为满足这一需求，对于车辆–地面系统，首先必须确保车辆行驶于地面时的可通行性，特别是车辆行驶于越野环境时，由于地面条件的复杂性、未知性，坡度、草木、地貌和水文状况等都对军用车辆的作战机动有很大的影响 [2] 。因此对地表土壤进行探测，获取地形土壤参数进而判断其可通行性是具有重要意义的工作。

本文综述了地表探测方法，对遥感技术和原位土壤探测技术进行了详细介绍，并对其优缺点进行比较分析。评分结果表明原位土壤探测方法(in situ soil sensing)得分最高，通过在地表土壤中布设轻量级的传感器节点可以快速准确全面地探测土壤属性，获取高质量的土壤参数。

无线传感器网络在战场侦查、环境生态监测、人员跟踪定位等方面有广泛应用 [3] 。土壤传感器可用于监测土壤属性，传感器节点一经布设将长期处于静止稳定状态，可以长时间实时监测，且监测数据能够清晰地反映土壤水分和土壤颗粒的组成信息，而且还对密度、酸碱度、营养物质的积累和温度等得出直观的结论，这些都是成本高昂的遥感技术无法具备的 [4] 。当区域范围很大，远远超出单个节点的无线通信范围时，必须布设大量的土壤传感器节点，为实现节点对区域的有效覆盖和自身定位，节点的优化布设是一个必须考虑的重要问题。

本文提出了基于三角形的传感器节点优化布设算法(TBAD)，首先将待监测区域进行三角形划分，然后在三角形子区域内确定参考锚节点(位置已知节点)的最优位置，最后将普通土壤传感器节点(位置未知)随机布设在各子区域内，最终实现所有节点的定位和对整个区域的监测覆盖。

在大范围区域内进行仿真，比较本文提出的优化布设算法与锚节点随机布设法的性能，结果表明，在不增大计算开销和硬件成本(锚节点个数相同)的前提下，优化布设策略比随机布设策略的监测覆盖率提高了10%，逐渐增大测距误差时，定位精度的提高幅度亦增大，当测距误差为10% R (R为传感器节点的通信半径)时，定位精度提高了约6% R。

2. 地表土壤探测方法

越野环境对车辆行进机动性的影响因素包括坡度、土壤类型、土壤强度、植被、河流、障碍物、表面湿滑度、含水量、降雨雪等。下面介绍地表土壤属性的探测方法，总体而言探测方法分为两大类：一类是遥感技术；一类是原位土壤探测，具体分类见图1。

Figure 1. Curve: system result of standard experiment

图1. 地表土壤探测技术分类

2.1. 遥感技术

遥感技术是20世纪60年代兴起的一种探测技术，可以从星载(人造卫星)、局部(飞机或其他飞行器)两种方式对远距离目标所辐射的电磁波、可见光、红外线等进行收集、处理，并最后成像，从而对地面各种景物进行探测和识别。目前为止，遥感技术是地表属性数据的主要来源，地表植被、土壤中的黏土含量及含水量等可以利用卫星遥感技术获得，例如地球同步卫星可以提供高清的三维图像，目前西方一些国家正试图利用卫星对全球土壤的松软程度进行评估 [5] 。遥感技术可以细分为热惯性技术、雷达技术、光学技术等。

由于不同地表类型(岩石，土壤，植被，湖泊等)对温度变化的反应也不同，热惯性是其表面随温度变化滞后性的量度， [6] 利用热惯性特征来对地表土壤类型进行区分。目前热惯性技术所能达到的分辨率仍然比较低，尚无法用于地表可通行性的预测。

雷达遥感通过自身器件发射电磁波、再由雷达自身接收被反射回的电磁波回波，精确测距定位锁定地面物体，其电磁波成像比光学成像更高清抗干扰。雷达技术的先进之处在于对冰、雪、森林、土壤具有一定的穿透力，例如地面穿透雷达(Ground Penetrating Radar, GPR)的穿透深度可以超过30米 [7] ，且能够全天候、全天时工作，可以根据各种地物特殊的波谱特征有效区分地表类型，但其分辨率比较低。

光学立体成像技术收集的数据不需要额外的图像处理提取，可以直观获得地表的3D信息，可以从更大范围上了解地表环境和分类。例如LIDAR扫描仪 [8] 可以收集数据直接获取3D图像，不需要额外的图像处理提取过程，广泛用于3D地形表示、障碍回避、地形特征(地面覆盖物、树、灌木丛、岩石、高草等)提取等应用中。

2.2. 原位土壤探测

不同地表类型对应的车辆可通行性也不同，其支撑车辆通行的能力依赖于原位土壤的强度，为了确定土壤强度，首先要测量土壤的参数，然后将参数代入经验模型、半经验模型甚至理论分析模型来计算强度并预测车辆的机动性。原位土壤探测技术可以进一步分为间接测量技术和直接测量技术。

间接测量技术分为土壤力学的半经验模型 [9] 和震波技术 [10] 。半经验模型假定地表物质连续均匀分布、特征一致，通过对地表(土壤)进行测试以获取影响车轮与土壤交互性能的土壤参数，进而根据土壤力学提出的半经验预测模型来计算车轮(轮式或履带)在地面行进时对地表的作用力。

震波技术例如震波折射谱分析已经广泛用于工程地质研究，通过对收集到的地震波谱进行分析可以获得地面及次表面的地层结构，例如识别底层坚实(岩床)表层松软或者底层凹陷表层平坦的土壤。

原位土壤直接测量是评估土壤强度的重要方法，广泛采用的是圆锥探测仪和Bevameter技术 [11] 。圆锥探测技术是由美国陆军水道试验站(Water ways Experiment Station, WES)提出，该技术利用静态的圆锥探测仪来获取土壤在单位面积上的摩擦阻力锥面指数(Cone Index, CI)以评估土壤的可通行性 [5] 。对圆锥指数评估机动性能进行了综述。Bevameter测量技术同时用到了压板与剪切环，其中压板用于测量土壤的镇压能力，剪切环用于确定土壤的剪切特征。Bekker在“压力—沉陷”关系的基础上对车辆与土壤的相互作用进行力学分析，通过确定和测量适当的土壤性质，推导出包含车辆和土壤参数的简化方程式 [12] 。

2.3. 比较分析

为了定量比较两类地表探测方法的优缺点，将其性能细化为以下10个指标 [4] ：1) 评估的土壤参数个数：方法所能直接/间接测量出的土壤参数的个数。2) 顶层土壤特征和属性识别。3) 次表层土壤特征和属性识别：顶层土壤之下的土壤参数类型，可能是硬土、岩床，也可能是松软土壤。4) 可以穿透的土壤深度。5) 数据处理时间：该参数决定了地表属性的探测是否实时。6) 仪器校准需求。7) 区域覆盖面积：给定地表环境，该参数是指不同方法单次探测所能覆盖的区域面积。8) 分辨率：该参数决定了表层/次表层土壤属性数据的精度(分辨率)。9) 传感器数量：对于需要布设传感器的探测方法而言，传感器的数量对于系统的设计和布设是一个必须考虑的重要参数，决定了系统的造价。10) 能量需求。11) 系统耗时：从系统布设到获取地表层/次表层土壤属性的时间。

根据上述参数对不同地表土壤监测方法进行评分，每个参数对应差、中、良三个等级，对应的分值为1、2、3，详细的评分标准见表1，评分结果见表2。

从表2可以看出，遥感技术与原位土壤探测相比较而言，后者可以有效提取地表土壤特征，进而识别车辆行进中的潜在危险(例如，松软土壤导致的车辆沉陷)，这一点是星载遥感技术和光学技术不能实现的。其中得分最高的是原位土壤直接测量技术，这表明轻量级的可直接快速部署的传感器能够提供高质量的土壤参数数据，为我们进一步研究和监测土壤属性指明了方向。

Table 1. The standard of scoring

表1. 评分标准

Table 2. Comparison of different terrain soil sensing methods

表2. 地表土壤监测方法比较

3. 传感器优化布设

无线传感器节点通过配置各种传感器(例如水分、温度等)可以准确获得土壤属性，并将采集的土壤数据和节点自身的位置通过无线网络实时传输到后台基站或区域内行驶的越野车辆上，为地表土壤监测和越野路径选择提供参数依据。

没有位置属性的感知信息将失去利用价值 [3] ，为了动态监测野外给定区域的地表土壤属性，必须首先确保布设在区域内的节点能够得到有效定位，当区域范围很大远远超出无线节点的通信范围时，我们采用分而治之的策略，将大区域划分为若干子区域，使每个子区域都位于单跳通信范围内，然后在各子区域内的寻找锚节点(位置已知的参考节点)的最优位置，最后在各子区域内随机布设普通传感器节点。这里涉及到两个关键问题：1) 区域的划分；2) 锚节点位置的选择。

3.1. 区域的划分

在二维定位场景中，对于单个待定位节点而言，至少要接收三个锚节点的位置广播并测量与之距离才能解算出自身的位置，因此，对于区域而言，至少达到3-覆盖才能实现区域任一位置处的节点可定位，即区域中任一位置处都可以接收到至少三个锚节点的位置广播。

3.1.1. 子区域的形状

关于区域的划分，子区域形状的选择问题可以转化为何种正多边形的内角可以等分一个圆周，我们有如下定理：

定理1：正n边形等分一个圆周，当且仅当n = 3，4，6。

证明：正n边形的内角为 $\frac{n-2}{n}\cdot {180}^{°}$ ，无缝拼接等分要求 ${360}^{°}\cdot \frac{n}{\left(n-2\right)\cdot {180}^{°}}=2+\frac{4}{n-2}$ 为整数，此时n

只能取3，4，6。证毕。

因此我们提出了以待定位区域质心为中心，进行正n边形划分的方法，n = 3，4，6，分别如下图2(a)~(c)所示，各区域的质心用“Ÿ”标识。

当正多边形完全位于待定位区域内时，将多边形的顶点作为锚节点的布设位置，在图3中用“§”标识；当某个正多边形没有完全被待定位区域覆盖时，我们将在3.2节详细讨论此种情况下如何选取锚节点的位置。

Figure 2. The partition of area

图2. 区域的划分

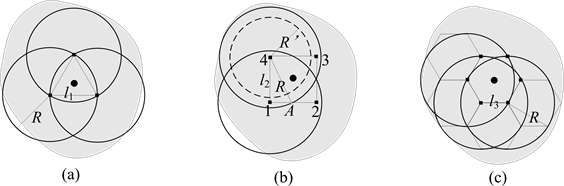
Figure 3. The decision of sub-area side length

图3. 子区域边长的选取

3.1.2. 子区域的边长

假定无线电信号传播符合单位圆盘模型(unit disk model)，通信半径为R。为了确保节点位于子区域内任意位置时均能够得到定位，对正n边形的边长亦有要求，由图3中的几何关系可知：

n = 3，当三角形的边长l₁ ≤ R时，可确保当锚节点布设在三角形顶点上时，三角形内任意位置处都可以接收到三个锚节点的广播位置(我们称之为3-覆盖)，反之，若l₁ > R，则三角形内总会存在无法被3-覆盖的位置，因此，三角形边长的最大值为R；

n = 4，为了确保正方形内任一点都可以被3-覆盖，要求四边形的边长 $l_2\le \frac{2R}{\sqrt{5}}$ 。可以验证，当 $R\ge \frac{\sqrt{5}}{2}{l}_2$

时3-覆盖条件满足，我们用反证法来说明该条件的必要性，在图3(b)中保持l₂不变，改变以锚节点为中

心的圆半径R大小，当 $R^{\prime }<\frac{\sqrt{5}}{2}{l}_2$ 时，正方形区域内存在不满足3-覆盖的点，例如点A，它只能接收到1、2号锚节点的位置广播，3、4号锚节点由于距离太远而失去作用，因此 $l_2\le \frac{2R}{\sqrt{5}}$ 是3-覆盖的必要条件；

当n = 6时，要求六边形的边长 $l_2\le \frac{2R}{\sqrt{5}}$ ，推导过程与n = 4的情形类似。

子区域边长选取的示意图如图3所示，“Ÿ”表示区域的质心，“§”表示锚节点的布设位置。

3.1.3. 正三角形划分

根据3.1.2节中所确定的多边形边长可计算出三角形的面积是 $\frac{\sqrt{3}}{4}{R}^2$ ，四边形面积为 $\frac{4R^2}{5}$ ，六边形面积为 $\frac{\sqrt{3}}{2}{R}^2$ ，下面我们来计算覆盖同样面积的待定位区域，各种划分方法所需要的锚节点个数。

假设三角形的个数为n₁，四边形个数为n₂，六边形个数为n₃，覆盖相同面积要求：

$\frac{\sqrt{3}}{4}{n}_1=\frac{4}{5}{n}_2=\frac{\sqrt{3}}{2}{n}_3$

此时， $n_1=\lceil 1.84\rceil n_2,n_1=2n_3$ ，即

$n_2=\frac{n_1}{2},n_3=\frac{n_1}{2}$ (1)

当三角形、四边形和六边形以如图4方式拼接时，相邻多边形间有两个公共顶点，那么n₁个三角形所需的锚节点数为n₁ + 2，n₂个四边形所需的锚节点数为2n₂ + 2，n₃个三角形所需的锚节点数为4n₃ + 2，根据式(1)的数值关系可知，用图4方式覆盖同样面积的区域，所需要的锚节点个数分别为n₁ + 2、n₁ + 2，2n₁ + 2。

从而可知，三角形划分与四边形划分所需要的锚节点个数相对较少，由于 $n_1=\lceil 1.84\rceil n_2$ 涉及到上取整，因此实际中三角形划分所需要的锚节点个数比四边形要少；而且对于图4中的三种区域划分方式，(a)中三角形划分，对于每个子区域而言，刚好提供了三个锚节点位置，实现3-覆盖，每个锚节点都最大限度地发挥了定位功效，信号覆盖的冗余度最小。

因此在确保区域中节点都可定位的前提下，从节省硬件和能耗开销角度考虑，三角形划分方式是最经济实用的布设方式。

3.2. 锚位置的选取

子区域划分完毕后，对于某个子三角形而言，若子三角形的顶点全位于待定位区域内，那么就将锚节点布设在顶点上；当三角形的顶点超出待定位区域时，首先我们证明，区域边界与该三角形的交点数至少为2。

定理2：对于凸区域而言，若三角形存在部分面积位于区域外，那么该三角形与区域边界的交点数至少为2。

证明：将凸区域边界上点的集合标记为À，将位于三角形内部的边界点的集合标记为À_in，位于三角形外部的边界点的集合记为À_out，任从À_in中取出一点记为v₁，从À_out中任取一点记为v₂，由于区域边界上的点是连续的，因此从v₁到v₂的区域边界À_v2-v1必然与三角形的某条边相交，记该点为v_intersect-1；从v₁到v₂后，继续沿着区域边界向前，将存在一点v_{3 $\in$} À_out，同理，区域边界À_v2-v3必然与三角形的某条边相交，记该点为v_intersect-2，命题得证。

因此，当三角形的顶点超出待定位区域时，用V_in表示位于待定位区域内的三角形顶点，V_out表示区域外的顶点，我们提出如下布设策略：

情况1：|V_in| = 0时

由定理2可知区域边界与三角形边界的交点数n >= 2，由于待定位区域为凸，因此，交点数为2，记这两个交点为v_intersect-1、v_intersect-2，此时从位于三角形内部的区域边界Àv_intersect-1-v_intersect-2中选出构成面积最大的一个点v_boundary，将三个锚节点布设在v_intersect-1、v_intersect-2和v_boundary上；

Figure 4. Stitching by sub-areas

图4. 子区域的拼接

情况2：|V_in| = 1时

区域边界与三角形边界的交点数记为n，由定理2可知n >= 2。若n = 2，我们将三个锚节点布设在V_in和另两个交点上；若n > 2，则从n + 1个点中(n个交点和三角形的一个顶点)选出覆盖面积最大的3个作为锚节点的布设位置；

情况3：|V_in| = 2时

由定理2可知区域边界与三角形边界的交点数n >= 2，此时从n + 2个点中(n个交点和三角形的两个顶点)选出覆盖面积最大的3个作为锚节点的布设位置。

图5表示三角形划分下的锚节点布设策略，“§”表示锚节点的布设位置，(a)为|V_in| = 0时，将锚节点布设在交点和边界上；(b)为|V_in| = 1时的情形；(c)为|V_in| = 2，此时由于交点数大于3-|V_in|，需要从两个交点中选择覆盖面积更大的一个作为第三个锚节点的布设位置；(d)为|V_in| = 3时，将锚节点布设在三角形的顶点上。

我们称图5所示的基于正三角形的锚节点布设策略为TBAD (Triangle Based Anchor Deployment)，下面我们证明TBAD可以确保布设在区域内任一位置处的待定位节点均可被至少三个锚节点覆盖，即整个区域都可定位。

定理3：上述布设策略TBAD，可确保待定位区域内任一位置处的节点均可定位。

证明：对图5中的各种布设情形而言，锚节点总是布设在三角形的顶点或内部；当三角形整体位于待定位区域内时，锚节点布设在三角形的顶点上，由三角形边长与通信半径R的关系可知，对于三角形内部任意点而言，总可被3-覆盖；当三角形部分位于待定位区域内时，将交叠区域记为S_cover，S_{cover $\subset$} S_triangle，对S_cover内的任意两个点v₁，v₂而言，两点的直线距离l_v1-v2总小于R，即三角形的边长，因此无论三个锚节点布设在S_cover内的哪个位置，S_cover内的所有点都可以被3-覆盖。

综上，此种锚节点布设策略，可以确保待定位区域内的任一点均可定位。证毕。

3.3. 性能评价

为了评价大范围区域内传感器锚节点优化布设策略TBAD的性能，我们从两个方面与随机布设策略进行比较：1) 区域内传感器节点的定位覆盖率(可定节点占节点总数的比例)；2) 区域内节点的定位精度。

仿真配置：1000米 × 1000米的的区域随机布设500个待定位传感器节点，锚节点和待定位节点的通信半径R相同，为200米。在优化布设方法中，先将区域等分为边长等于R的正三角形，然后依据TBAD布设策略设置锚节点的位置，可知需要布设的锚节点数为45个，见图6中的正方形节点；在随机布设方法中，我们将45个锚节点随机布设在区域中，单次布设情形见图6中的三角形节点，计算不同布设策略下的定位覆盖率和定位精度。

计算随机布设策略下的定位覆盖率时，我们将45个锚节点随机布设在500个节点的随机网络中，计算每次布设下的覆盖率，然后蒙特卡罗仿真1000次取各次覆盖率的平均值作为最终结果。暂不考虑已定位节点升级为锚节点进而定位其他待定位节点的情形，我们认为若待定位节点的一跳邻居数少于3个就为无法定位节点。仿真结果表明，对于随机布设策略而言，定位覆盖率约为90%；对于优化布设策略TBAD而言，定位覆盖率为100%，与理论分析结果相一致。

假设锚节点与待定位节点间的测距误差服从零均值的高斯同分布N(0,s²)，定位精度使用网络中所有节点的均方根误差RMS来衡量。蒙特卡罗仿真1000次，取平均RMS作为最终结果，如图7所示。横坐标表示测距误差，纵坐标表示定位误差RMS，从中可明显看出，锚节点优化布设策略TBAD下的定位精度比随机策略要高很多，而且随着测距误差的增大，定位精度的提高越显著，当测距误差为20米(10%R)

Figure 5. Anchor deployment strategies

图5. 锚节点布设策略

Figure 6. Anchor deployment of different strategies

图6. 不同布设策略的锚节点分布

Figure 7. Comparison of localization accuracy between different strategies

图7. 不同布设策略的定位精度对比

时，锚节点优化布设策略TBAD对应的定位误差比随机策略小12米，相较于信号传播半径R = 200米而言，定位精度提高了6% R。

4. 结束语

地表土壤对越野车辆的机动性具有重要影响，为确保车辆行驶时地表的可通行性，必须对地表土壤属性进行探测。本文首先对土壤探测技术进行详细介绍并比较其优缺点，结果表明通过布设轻量级的传感器可以直接有效探测土壤属性，具有遥感及间接探测技术所没有的优势。基于此我们提出了土壤传感器节点的优化布设方案，仿真结果表明该方案既能保证对监测区域的覆盖率又提高了节点自身的定位精度，具有实际的应用价值。

基金项目

国家自然科学基金(61273047，61573376)。