MO^¨ bius立方体的h-好邻条件诊断度

The h-Good-Neighbor Conditional Diagnosability of MO^¨ bius Cubes

摘要:

条件诊断度是衡量互连网络可靠性能优劣的重要参数，“条件”意味着任何处理器的所有相邻处理器不能同时出现潜在故障。作为条件诊断度的一个改进参数，Peng等人通过限制要求每个无故障节点至少包含有h个无故障的邻点提出了h-好邻条件诊断度，是一种在节点失效的情况下衡量互连网络可靠性的重要指标。本文研究并证明了Möbius立方体(MN_Q)在PMC模型和MM*模型下的h-好邻条件诊断度是(n-h+1)2^h-1(0≤h≤n-3)，相比于传统诊断度成几何倍数的提高。

Abstract: The conditional diagnosability is an important measure of the reliability of interconnection network. The “condition” means that all adjacent processors of any processor cannot be potentially faulty at the same time. As an improvement of conditional diagnosability, h-good-neighbor conditional diagnosability has been proposed by Peng et al. under the assumption that every fault-free node has at least h fault-free neighbors, which is an important indicator of reliability of interconnection network in the case of vertices failure. In this paper, we first introduced and investigated the h-good-neighbor conditional diagnosability of Möbius Cubes (MN_Q). And we showed that the h-good- neighbor conditional diagnosability of Mo ̈bius Cubes is (n-h+1)2^h-1(0≤h≤n-3) under the PMC and MM* model, which can be several times higher than the classical diagnosability of MN_Q.

1. 引言

随着大规模集成电路和现代通讯技术的快速发展，多处理器计算机系统中处理器的数量急剧增加，连接这些处理器的互连网规模也在相应扩大。再加上各种因素及外界因素的干扰，系统不可避免的会发生故障，那么如何在系统发生故障时，仍能使系统高效、快速、准确地正常工作，减轻系统故障风险是具有极其重要的现实意义。在多处理器系统中故障诊断是一个用来分析系统故障诊断和定位能力的强有力工具。确定一个系统中的故障节点和无故障节点的过程叫做系统的故障诊断，系统可以保证确定的最大故障节点数称为系统可诊断度 [1] [2] 。

在系统故障诊断中，根据互连网络拓扑结构充分运用处理器之间的自治能力，让各个处理器相互测试，由测试结果得到准确的诊断结果。不同的测试假设导致不同的测试模型。一般常用的两种模型为PMC模型和MM*模型。1967年，Preparata et al. [1] 假设只有在处理器相邻时才可以相互测试的情况下提出了PMC模型。在该模型中，当执行测试者u是无故障时，若被测试者v是无故障的，那么测试的结果为0，否则为1，此时测试的结果是可靠的。当测试者u故障时，测试结果不定，此时测试的结果是不可靠的。1981年Malek和Maeng [3] 提出了比较模型，简称MM模型。在MM模型下，测试也是相邻处理器之间相互测试，如果执行测试者w是无故障的，那么测试的结果是可靠的，即当被测试者u，v都无故障时，测试结果为0，否则为1；反之，当测试者w故障的，测试结果是不可靠的，即测试结果不定。1992年，Sengupta和Dahbura [4] 对MM模型进行了改进，要求每一个处理器节点都必须与它的所有的相邻节点互相测试，称为MM*模型。表1描述了在PMC模型与MM*模型下相邻节点的测试结果。

由于t-可诊断的充分条件要求较高，不仅受诊断图的最小度限制，而且相比于系统中的总节点数，t

Table 1. The test results under the PMC model and MM* model

表1. PMC和 MM*模型下的测试结果

值显得非常小。如超立方网络中，t-可诊断度受其最小度限制，可诊断性 $n/2^n$ 相对很小。由于系统中点数众多，出现故障的点数可能会很多，此时t-可诊断并不适用。为了进一步提高系统的可诊断度，以牺牲精确诊断为代价，Lai等人于2005年通过限制每一个节点至少有一个好的邻点提出了条件t-可诊断 [5] 。因为在实际环境中，一个点的所有的邻点同时故障的可能性相对较小，几乎可以忽略不计，故此，我们认为这种策略是可行的。但对于大规模的多处理器系统，一个节点的度远大于1，这时仍要求一个节点至少有一个好邻点相对保守，同时也无益于在实际环境中提高系统的可诊断度。于是Peng等人 [6] 提出了h-好邻条件诊断度，并同时确定了当 $0\le h\le n-3$ 时，超立方体在PMC模型下的-好邻条件可诊断度为 $\left(n-h+1\right)2^h-1$ 。随之超立方体、k-元n-方立方体、排列组合图等网络拓扑结构在PMC模型和MM*模型下的h-好邻条件诊断度被广泛研究并确定 [7] [8] [9] [10] 。研究发现该策略诊断相对传统诊断度而言诊断能力成几何倍数的提高，大大提高了系统的可靠性。

另外，Möbius立方体网络作为超立方体网络的变体，在保留前者原有优良性能的基础上，又增加了一些新的优良性能。本文主要研究了Möbius立方体在PMC模型和MM*模型下h-好邻条件诊断度并确定了当 $0\le h\le n-3$ 时，其在PMC和MM*模型下的h-好邻条件可诊断度为 $\left(n-h+1\right)2^h-1$ 。

2. 预备知识

对多处理器计算机系统进行理论研究时，通常可看作一个简单无向图 $G=\left(V,E\right)$ ，其中点集V代表系统中处理器的集合，边集E代表系统中处理器间的通信链路的集合。本节首先引入了本文中所应用的图论相关定义及相关性质，然后对M bius立方体网络拓扑结构进行了简要描述。

2.1. 术语和概念

在本文中图 $G=\left(V,E\right)$ 是指一个顶点集为V边集为E的无环无平行边的简单连通图。对于任意的两点u和v，如果存在边 $e=\left(u,v\right)\in E\left(G\right)$ ，则我们说他们是相邻的，也可以说边e连接了顶点u和v。对于 $\forall u\in V$ ，用 $N_G\left(u\right)$ 表示u在G中的邻点集。点u的度是指u所关联的边的数目，即是在 $N_G\left(u\right)$ 中点的数

目，记为 $d_G\left(u\right)$ 。 $\forall S\subseteq V$ ，用 $N_G\left(S\right)$ 表示 $S$ 在 $G-S$ 中的邻点集，即 $N_G\left(S\right)={\displaystyle {\cup }_{u\in S}{N}_G\left(u\right)-S}$ 。对于图

$H=\left(V^{\prime },E^{\prime }\right)$ ， $G=\left(V,E\right)$ ，如果 $V^{\prime }\subseteq V$ 且 $E^{\prime }\subseteq E$ ，则称图H为G的子图，记为 $H\subseteq G$ 。若 $V^{\prime }=V$ ，此时则称子图H为G的支撑子图。对于图G中任意子集 $V^{\prime }\subseteq V\left(G\right)$ ，称以 $V^{\prime }$ 为点集，以图G中两端点均在 $V^{\prime }$ 的所有边为边集的子图为点集 $V^{\prime }$ 的导出子图，记作 $G\left[V^{\prime }\right]$ 。给定两个集合A，B，集合 $\left(A-B\right)\cup \left(B-A\right)$ 称为A与B的对称差，记为 $A\Delta B$ 。用 $G-A$ 表示从图G中删除顶点子集A所获得的子图，记为 $\bar{A}$ 。这里涉及未提到的术语可参考文献 [11] 。

DahBura与Masson [12] 提出了一个多项式复杂度算法来检验一个系统是否是t-可诊断的。

引理2.1 [12] ：多处理器系统 $G=\left(V,E\right)$ 中，若任意一对不同的故障集 $F_1,F_2\subseteq V$ 满足 $\left|F_1\right|,\left|F_2\right|\le t$ ，且在 $V-\left(F_1\cup F_2\right)$ 和 $F_1\Delta F_2$ 之间至少有一个测试，则称系统G是t-可诊断的。

Lai et al. [5] 与Sengupta等人 [4] 分别提出了在PMC模型和MM*下故障集对 $\left(F_1,F_2\right)$ 可区分的充要条件。图1(a)，图1(b)分别给出了在PMC模型和MM*下可区分对 $\left(F_1,F_2\right)$ 的示例说明，即引理2.2和2.3。

引理2.2 [5] ：对图 $G=\left(V,E\right)$ 的任意两个集合 $F_1,F_2\subseteq V$ ，若 $V-\left(F_1\cup F_2\right)$ 中存在一个点u与点 $v\in F_1\Delta F_2$ 相邻，则称 $F_1$ 与 $F_2$ 在PMC模型下是可区分的。

由引理2.1，2.2可知，若系统 $G=\left(V,E\right)$ 中任意两个不同的子集 $F_1,F_2\subseteq V$ 有 $\left|F_1\right|,\left|F_2\right|\le t$ ，且 $F_1$ 与 $F_2$ 是可区分的，则该系统是t-可诊断的。

引理2.3 [4] ：对图 $G=\left(V,E\right)$ 的任意两个集合 $F_1,F_2\subseteq V$ ， $F_1,F_2$ 在MM*模型下可区分当且仅当以下条件至少一个成立：

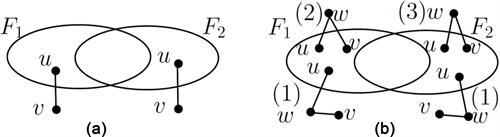
Figure 1. Illustration of a distinguishable pair $\left(F_1,F_2\right)$

图1. 可区分对 $\left(F_1,F_2\right)$ 的说明

1) 存在点 $u\in \left(F_1\Delta F_2\right)$ ， $v,w\in \overline{F_1\cup F_2}$ 满足 $uw,vw\in E\left(G\right)$ 。

2) 存在点 $u,v\in \left(F_1-F_2\right)$ ， $w\in \overline{F_1\cup F_2}$ 满足 $uw,vw\in E\left(G\right)$ 。

3) 存在点 $u,v\in \left(F_2-F_1\right)$ ， $w\in \overline{F_1\cup F_2}$ 满足 $uw,vw\in E\left(G\right)$ 。

定义2.1 [6] ：设 $G=\left(V,E\right)$ 是一个简单无向图， $F\subseteq V$ 。若 $\forall v\in V-F$ 有 $\left|N\left(v\right)\cap \left(V-F\right)\right|\ge h$ ，则称F是图G的h-好邻条件故障集。若图G的h-好邻条件故障集F使得 $G-F$ 不连通，则称F是图G的h-好邻条件故障点割集。G的所有h-好邻条件故障点割集中最小基数称为G的h-好邻连通度，记为 ${\kappa }^h\left(G\right)$ 。

定义2.2 [6] ：设 $G=\left(V,E\right)$ 是一个简单无向图，若任意一对不同的h-好邻条件故障集 $F_1,F_2\subseteq V$ 满足 $\left|F_1\right|,\left|F_2\right|\le t$ ，且 $F_1,F_2$ 是可区分的，则称图G是h-好邻条件t-可诊断的。使得图G是h-好邻条件t-可诊断的最大t值称为图G的h-好邻条件可诊断度，记作 $t_h\left(G\right)$ 。

2.2. Möbius立方体网络

超立方体网络 $Q_n$ 作为当今研究的热点，具有正则性、对称性、顶点传递性、高容错性等优良特性，正是这些特性使得它成为并行处理和并行计算系统的首选拓扑结构。但是超立方体网络同样也存在一些不足，比如其直径相对较大，在其维数增加时易造成数据传输的丢失，成本花费较高等 [13] 。因此，莫比乌斯立方体网络 [14] 作为超立方体的变体结构被提出，它有更优与超立方体的性能，尤其在直径、连通度、容错性、嵌入性等方面。

1995年，Cull和Larson [14] 提出了n-维莫比乌斯(Möbius)立方体网络，记为 $M{Q}_n$ ，具有以下性质：(详见文献 [14] )。这里用2元n序列来定义。

定义2.3 [14] ：n-维Möbius立方体网络的顶点可以由一个n位二进制串表示，即

$V=\left\{u_{n-1}{u}_{n-2}\cdots u_0|u_i\in \left\{0,1\right\},i=0,2,\cdots ,n-1\right\}$

点 $u=u_{n-1}{u}_{n-2}\cdots u_0\in V\left(M{Q}_n\right)$ 连接到另外n个点 $u^i\in V(M{Q}_n)$ ( $0\le i\le n-1$ )当且仅当：

$u^i=\{\begin{array}{l}{u}_{n-1}{u}_{n-2}\cdots u_{i+1}\overline{u_i}{u}_{i-1}\cdots u_0;u_{i+1}=0;\\ u_{n-1}{u}_{n-2}\cdots u_{i+1}\overline{u_i{u}_{i-1}\cdots u_0};u_{i+1}=1.\end{array}$

其中 $\overline{u_i}=1-u_i$ 。

根据Möbius立方体的定义，我们可以确定两个顶点是否相邻。因此，当 $u_n=0$ 时，我们称网络为0-Möbius立方体(0-MQ_n)，当 $u_n=1$ 时，该网络称为1-Möbius立方体(1-MQ_n)。

引理2.4 [15] ： $n\ge 3$ ，n-维Möbius立方体 $M{Q}_n$ 无三角。

引理2.5 [16] ：设 $Y\subseteq V\left(X{Q}_n\right),X{Q}_n\in H{L}_n$ ， $n\ge 1$ ，若 $\delta \left(X{Q}_n\left[Y\right]\right)\ge h$ ，则 $\left|Y\right|\ge 2^h$ ， $h\in \left[0,n\right]$ 。

引理2.6 [17] ：若 $X{Q}_n\in \left\{C{Q}_n,0-M{Q}_n,1-M{Q}_n,LT{Q}_n\right\}$ ， $n\ge 2$ ，则 ${\kappa }^h\left(X{Q}_n\right)=2^h\left(n-h\right)$ ， $h\in \left[0,n-2\right]$ 。

3. Möbius立方体的h-好邻条件可诊断度

在本节中，我们将证明我们的主要结论：n-维Möbius立方体在PMC模型和MM*模型下的h-好邻条件诊断度。

定理3.1：n-维M bius立方体在PMC模型和MM*模型下的h-好邻条件诊断度 $t_h\left(M{Q}_n\right)$ 的上界，即 $t_h\left(M{Q}_n\right)\le 2^h\left(n-h\right)+2^h-1$ ， $0\le h\le n,n\ge 2$ 。

证明：设 $A=\left\{x=x_{n-1}{x}_{n-2}\cdots x_h{x}_{h-1}\cdots x_0|x_i=0,i\in \left\{h,h+1,\cdots ,n-1\right\}\right\}$ ， $x_j\in \left\{0,1\right\}$ ， $j\in \left\{0,1,\cdots ,h-1\right\}$ 。显

然地， $M{Q}_n\left[A\right]\cong M{Q}_h$ ， $\left|A\right|=2^h$ 。由 $M{Q}_n$ 的定义知， $A$ 的所有邻点在 $V_k$ 中，这里 $V_k=\left\{x^k|x\in A\right\}$ ， $k\in \left\{h,h+1,\cdots ,n-1\right\}$ 。记 $F_1={\displaystyle {\cup }_h^{n-1}{V}_k}$ ， $F_2=A\cup F_1$ 。所以有 $\left|F_1\right|=\left(n-h\right)2^h$ ， $\left|F_2\right|=\left(n-h\right)2^h+2^h$ 。由于 $A=F_1\Delta F_2$ 和 $F_1=N\left(A\right)$ ，所以在 $\overline{F_1\cup F_2}$ 和 $F_1\Delta F_2$ 之间不存在边的连接，故根据引理2.2与2.3知， $F_1$ 和 $F_2$ 是不可区分的。如图2所示。

另一方面， $M{Q}_n\left[A\right]\cong M{Q}_h$ ，很容易得到 $M{Q}_n\left[A\right]$ 是h-正则图，所以在A中的每个点至少有h个邻点在A中。记 $X=V\left(M{Q}_n\right)-F_1\cup F_2$ ，因为 $F_1\subset F_2$ ，所以 $X=V\left(M{Q}_n\right)-F_2$ 。现在我们考虑在X中的点，由X的定义知，对 $\forall x\in X$ 有 $x^i\in X$ ， $i\in \left\{0,1,\cdots ,h-1\right\}$ ，即在X中的每个点至少有h个邻点在X中。因此， $M{Q}_n-F_1$ 与 $M{Q}_n-F_2$ 的最小度都至少为h，由定义2.1知， $F_1$ 与 $F_2$ 是两个不同的h-好邻条件故障点割集。

观察到 $F_1$ 和 $F_2$ 是 $M{Q}_n$ 的两个不同的h-好邻条件故障点割集且 $\left|F_1\right|=\left(n-h\right)2^h$ ， $\left|F_2\right|=\left(n-h\right)2^h+2^h$ ，但是 $F_1$ 和 $F_2$ 是不可区分的。因此，根据引理2.2与2.3知， $M{Q}_n$ 不是h-好邻条件 $2^h\left(n-h\right)+2^h$ -可诊断的。即有 $t_h\left(M{Q}_n\right)\le 2^h\left(n-h\right)+2^h-1$ 。因此，定理成立。

上述定理提供了 $M{Q}_n$ 的h-好邻条件可诊断的一个上界。下面我们分别证明在PMC模型和MM*模型下下界是可以达到的。

定理3.2：n-维Möbius立方体在PMC模型下的h-好邻条件诊断度的下界 $t_h\left(M{Q}_n\right)\ge 2^h\left(n-h\right)+2^h-1$ ， $0\le h\le n-3,n\ge 2$ 。

证明：反证法，假设 $t_h\left(M{Q}_n\right)<2^h\left(n-h\right)+2^h-1$ ，则存在两个不可区分的h-好邻条件故障集 $F_1,F_2$ 使得 $\left|F_1\right|,\left|F_2\right|\le 2^h\left(n-h\right)+2^h-1$ 。且当 $0\le h\le n-3$ 时，易知 $\left|V\left(M{Q}_n\right)\right|-\left|F_1\cup F_2\right|\ge 2^n-2\left(2^h\left(n-h\right)+2^h-1\right)>0$ ，

Figure 2. Illustration of $F_1$ and $F_2$

图2. $F_1$ 和 $F_2$ 的说明

所以有 $\overline{F_1\cup F_2}\ne \varnothing$ 。因为 $F_1$ 与 $F_2$ 是不可区分的，由引理2.2可知在 $F_1\Delta F_2$ 和 $\overline{F_1\cup F_2}$ 之间是不存在边的连接，因此 $N\left(F_1\Delta F_2\right)\subseteq F_1\cap F_2$ 。且又因为 $F_1$ 与 $F_2$ 是两个不同的h-好邻条件故障集，所以 $M{Q}_n-F_1$ 与 $M{Q}_n-F_2$ 的最小度都至少为h，故 $F_1\cap F_2$ 是 $M{Q}_n$ 的一个h-好邻条件故障点割集。结合引理2.5和2.6得， $M{Q}_n$ 的最小点割集的基为 $\left(n-h\right)2^h$ 。因此， $\left|F_1\cap F_2\right|\ge {\kappa }^h\left(M{Q}_n\right)=\left(n-h\right)2^h$ 。

由于 $F_1$ 是一个h-好邻条件故障集，在 $F_2-F_1$ 中的任意点至少有h个好邻点在子图 $F_2-F_1$ 中，即 $\delta \left(F_2-F_1\right)\ge h$ ，结合引理2.5有 $\left|F_2-F_1\right|\ge 2^h$ 。此时，

$\left|F_2\right|=\left|F_2-F_1\right|+\left|F_1\cap F_2\right|\ge 2^h+\left(n-h\right)2^h$

矛盾于假设 $\left|F_2\right|\le 2^h+\left(n-h\right)2^h-1$ 。因此，定理成立。

定理3.3：n-维Möbius立方体在MM*模型下的h-好邻条件诊断度的下界 $t_h\left(M{Q}_n\right)\ge 2^h\left(n-h\right)+2^h-1$ ， $0\le h\le n-3,n\ge 5$ 。

证明：反证法，假设 $t_h\left(M{Q}_n\right)<2^h\left(n-h\right)+2^h-1$ ，则存在两个不可区分的h-好邻条件故障集 $F_1,F_2$ 使得 $\left|F_1\right|,\left|F_2\right|\le 2^h\left(n-h\right)+2^h-1$ 。由引理2.3知，故障集对 $\left(F_1,F_2\right)$ 不能满足引理2.3的任一条件，故我们将证明以下每一种情况都与假设相矛盾。

情形1： $V\left(M{Q}_n\right)=F_1\cup F_2$ 。

当 $n\ge 5,0\le h\le n-3$ 时，因为 $V\left(M{Q}_n\right)=F_1\cup F_2$ ，此时，

$2^n=\left|V\left(M{Q}_n\right)\right|=\left|F_1\cup F_2\right|\le \left|F_1\right|+\left|F_2\right|\le 2\left(2^h\left(n-h\right)+2^h-1\right)\le 2^n-2$

这与事实相矛盾。

情形2： $V\left(M{Q}_n\right)\ne F_1\cup F_2$ 。

在此情形下，我们有 $V\left(M{Q}_n\right)-F_1\cup F_2\ne \varnothing$ 。设 $W$ 是 $V\left(M{Q}_n\right)-F_1\cup F_2$ 的所有孤立点的集合。则对

$\forall w\in W$ ，有 $N_{M{Q}_n}\left(w\right)\subseteq F_1\cup F_2$ 。下面我们根据h的大小讨论以下两种情形来证明 $W=\varnothing$ 成立。

子情形2.1： $h=1$ 。

反证法，假设 $W=\varnothing$ ，则至少存在一个孤立点 $w\in W$ 。若 $F_1-F_2=\varnothing$ ，则有 $w\in V\left(M{Q}_n\right)-F_2$ ， $N_{M{Q}_n}\left(w\right)\subseteq F_2$ 。这与 $F_2$ 是h-好邻条件故障集相矛盾，所以 $F_1-F_2\ne \varnothing$ 。类似地， $F_2-F_1\ne \varnothing$ 。由于 $F_1$ 和 $F_2$ 是两个不可区分的故障集，根据引理2.3得，至多存在一个点 $u\in F_2-F_1$ 使得u与w是相邻的，故恰好存在一个点 $u\in F_2-F_1$ 使得u与w是相邻的。类似地，恰好存在一个点 $v\in F_1-F_2$ 使得v与w是相邻的。因此，W中的任意点存在 $n-2$ 个邻点在 $F_1\cap F_2$ 中。由假设知 $\left|F_2\right|\le 2^h\left(n-h+1\right)-1=2n-1$ ，所以有：

$\begin{array}{c}\underset{w\in W}{{\displaystyle \sum }}\left|N_{F_1\cap F_2}\left(w\right)\right|=\left|W\right|\left(n-2\right)\le \underset{v\in F_1\cap F_2}{{\displaystyle \sum }}{d}_{M{Q}_n}\left(v\right)\\ \le \left|F_1\cap F_2\right|n\le \left(\left|F_2\right|-1\right)n\le \left(2n-2\right)n\end{array}$

由上可得， $\left|W\right|\le 2n+2$ 。如果 $V\left(M{Q}_n\right)-\left(F_1\cup F_2\cup W\right)=\varnothing$ ，则当 $n\ge 5$ 时，

$\begin{array}{c}{2}^n=\left|V\left(M{Q}_n\right)\right|=\left|F_1\cup F_2\right|+\left|W\right|\le \left|F_1\right|+\left|F_2\right|+\left|W\right|\\ \le 2\left(2n-1\right)+2n+2<2^n\end{array}$

不成立，所以 $V\left(M{Q}_n\right)-\left(F_1\cup F_2\cup W\right)\ne \varnothing$ 。记 $H=V\left(M{Q}_n\right)-\left(F_1\cup F_2\cup W\right)$ ，考虑到在 $V\left(M{Q}_n\right)-\left(F_1\cup F_2\right)$ 中的所有孤立点都包含在W中，所以不存在孤立点在H的导出子图 $M{Q}_n\left[H\right]$ 中。由引理2.3得，在H和 $F_1\Delta F_2$ 之间不存在边的连接。因为 $F_1$ 和 $F_2$ 都是1-好邻条件故障集，易知 $F_1\cap F_2$ 是 -好邻条件故障点割集。由引理2.5和2.6得， $\left|F_1\cap F_2\right|\ge 2n-2$ 。注意到 $\left|F_1\right|\le 2n-1$ ， $\left|F_2\right|\le 2n-1$ 且 $F_1-F_2\ne \varnothing$ ， $F_2-F_1\ne \varnothing$ 。因此， $\left|F_1-F_2\right|=\left|F_2-F_1\right|=1$ ，故设 $F_1-F_2=\left\{v_1\right\}$ ， $F_2-F_1=\left\{v_2\right\}$ 。对任意点w，w与 $v_1,v_2$ 是相邻的，且有

$N_{F_1\cap F_2}\left(w\right)=d_{M{Q}_n}\left(w\right)-\left\{v_1,v_2\right\}$ 。由于 $V\left(M{Q}_n\right)$ 中任意两个顶点之间至多有两个公共邻点，因此，至多在W中存在两个孤立点。图3给出了W的两种情形。

若 $\left|W\right|=1$ ，不防设 $W=\left\{w\right\}$ ，则 $w$ 与 $v_1,v_2$ 是相邻的。由引理2.4知 $M{Q}_n$ 中无三角且任意两个顶点之间至多有两个公共邻点，故有 $N_{F_1\cap F_2}\left(w\right)\cap N_{F_1\cap F_2}\left(v_1\right)=\varnothing$ ， $N_{F_1\cap F_2}\left(w\right)\cap N_{F_1\cap F_2}\left(v_2\right)=\varnothing$ 和 $N_{F_1\cap F_2}\left(v_1\right)\cap N_{F_1\cap F_2}\left(v_2\right)\le 1$ 。此时，当 $n\ge 4$ 时，

$\begin{array}{c}\left|F_2\right|=\left|F_1\cap F_2\right|+\left|F_2-F_1\right|\\ \ge \left|N_{F_1\cap F_2}\left(w\right)\right|+\left|N_{F_1\cap F_2}\left(v_1\right)\right|+\left|N_{F_1\cap F_2}\left(v_2\right)\right|-1+1\\ \ge n-2+n-1+n-1-1+1>2n-1\end{array}$

这与假设 $\left|F_2\right|\le 2n-1$ 相矛盾。

若 $\left|W\right|=2$ ，则 $N\left(\left\{v_1,v_2\right\}\cup W\right)\subseteq F_1\cap F_2$ 。不妨设 $W=\left\{w,w^{\prime }\right\}$ ，则 $w^{\prime }$ 与 $v_1,v_2$ 是相邻的。因为 $M{Q}_n$ 中任意两个顶点之间至多有两个公共邻点，所以 $v_1,v_2,w,w^{\prime }$ 在 $F_1\cap F_2$ 中无公共邻点。且当 $n\ge 4$ 时，

$2n-1\ge \left|F_2\right|=\left|F_1\cap F_2\right|+\left|F_2-F_1\right|\ge N\left(\left\{v_1,v_2\right\}\cup W\right)+1\ge n-8+1>2n-1$

不成立。

子情形2.2： $h\ge 2$ 。

由于 $F_1$ 是 $M{Q}_n$ 的h-好邻条件故障集，所以对任意的 $x\in V\left(M{Q}_n\right)-F_1$ 有 $\left|N_{V\left(M{Q}_n\right)-F_1}\left(x\right)\right|\ge h$ 。由假设知故障集对 $\left(F_1,F_2\right)$ 不满足引理2.3的任一条件，所以对于任意点 $w\in W$ ，至多存在一个邻点在 $F_2-F_1$ 中。因此， $\left|N_{\left\{V\left(M{Q}_n\right)-F_1\cup F_2\right\}}\left(w\right)\right|\ge h-1\ge 1$ ，即在 $V\left(M{Q}_n\right)-F_1\cup F_2$ 中的每个点都不是孤立点。

因此， $W=\varnothing$ 。

由 $W=\varnothing$ 知 $V\left(M{Q}_n\right)-F_1\cup F_2$ 中不存在孤立点，因此 $\left[V\left(M{Q}_n\right)-F_1\cup F_2\right]$ 中不存在边 $uv$ 使得 $u\left(v\right)$ 与

$F_1\Delta F_2$ 中的某些点是相邻的。否则， $F_1$ 和 $F_2$ 是可区分的，与假设矛盾。因此，在 $V\left(M{Q}_n\right)-F_1\cup F_2$ 和 $F_1\Delta F_2$ 之间不存在边。考虑到 $F_1$ 和 $F_2$ 是h-好邻条件故障集，易知 $F_1\cap F_2$ 是h-好邻条件故障点割集且 $\delta \left(M{Q}_n\left[F_2-F_1\right]\right)\ge h$ ，结合引理2.5和2.6得， $\left|F_2-F_1\right|\ge 2^h$ ， $\left|F_1\cap F_2\right|\ge {\kappa }^h\left(M{Q}_n\right)=\left(n-h\right)2^h$ 。此时，

$\left|F_2\right|=\left|F_2-F_1\right|+\left|F_1\cap F_2\right|\ge 2^h+\left(n-h\right)2^h$

Figure 3. Illustration of the proof of $h=1$

图3. $h=1$ 的证明情况说明

这与假设 $\left|F_2\right|\le 2^h+\left(n-h\right)2^h-1$ 相矛盾。

综上所述，定理成立。

由定理3.1，3.2和3.3，我们可以立即获得以下定理：

定理3.4：n-维Möbius立方体在PMC模型下的h-好邻条件诊断度 $t_h\left(M{Q}_n\right)=2^h\left(n-h\right)+2^h-1$ ， $0\le h\le n-3,n\ge 2$ 。

定理3.5：n-维Möbius立方体在MM*模型下的h-好邻条件诊断度 $t_h\left(M{Q}_n\right)=2^h\left(n-h\right)+2^h-1$ ， $0\le h\le n-3,n\ge 5$ 。

4. 结论

本文主要研究了n-维Möbius立方体 $M{Q}_n$ 的h-好邻条件诊断度，且分别确定了当 $n\ge 2$ 和 $n\ge 5$ 时，其在PMC和MM*模型下的h-好邻条件诊断度为 $t_h\left(M{Q}_n\right)=2^h\left(n-h+1\right)-1\left(0\le h\le n-3\right)$ 。h-好邻条件诊断度从本质上说限制的只是好的邻点，与条件t-可诊断是不同的。由于在大规模多处理器系统中，一个处理器相邻单元数远大于1，故其好的邻点会更多。所以该诊断策略更加适用于实际应用，是一个值得研究的方向，同时h-好邻条件诊断度的确定为后续算法的研究提供了更好的理论支撑。