基于微型传感器的近场辐射传热实验方法研究

Studying on the Experimental Method of Near-Field Thermal Radiation Based on Micro Sensors

摘要: 面向二氧化硅(SiO₂)材料开展了近场辐射传热实验测量方法研究，其核心工作是近场热辐射传感器设计。首先，基于电磁波理论以两个平行的SiO₂平板为对象分析近场热辐射的特性并以此确定近场热辐射传感器的关键参数；其次，根据近场热辐射的作用效果确定实验方案并设计相应的近场热辐射传感器；再次，基于经典传热理论确定实验模型，以及设计传感器的微加工工艺；最后，本实验方法在其他介质的近场辐射传热测量中的应用。

Abstract: The experimental method of near-field thermal radiation between two Silicon oxide (SiO₂) plates was developed. The key work is the near-field thermal radiation (NFTR) sensor design. Firstly, the character of the near field thermal radiation between two parallel SiO₂ plates was analyzed based on the electromagnetic wave theory, and the key parameter of the NFTR sensor was chosen. Se-condly, according to the difference effect of the thermal radiation emitter and the thermal radiation absorber, two kinds of experimental plan were made and the NFTR sensor was designed, separately. Thirdly, the experimental model was built by the classical heat transfer theory and the micromachining process of the NFTR sensor was developed. Finally, the experimental method was extended to evaluate the near-field thermal radiation between other medium.

1. 引言

具有一定温度的物体在其内部电子和离子的热运动的作用下会不断地从物体表面辐射出电磁波，在不同温度的物体之间由于温度差会导致其间的辐射传热 [1] 。进一步的，当上述物体的间距同等温度下黑体辐射的主波波长时(黑体温度300 K，热辐射主波波长为10 µm)会出现辐射传热明显增强的现象，即两物体间发生了近场热辐射现象 [2] [3] 。自20世纪60年代末发现近场热辐射现象以来，国内外科研团队基于微型探针技术开发了一些实验测量方法 [4] [5] [6] [7] [8] ，同时也有团队采用低导热材料或悬空薄膜结构开展了近场辐射传热的实验测量 [9] [10] 。本文作者是利用悬空薄膜结构微型传感器开展近场辐射传热测量实验的设计者之一，当时的实验目的是减少近场热辐射现象对微米纳米结构传感器绝热性能的影响，为传感器结构设计提供参考。本文将以二氧化硅材料为例阐述传感器设计过程，为利用微型传感器面向不同材料开展近场辐射传热测量提供参考。

2. 近场热辐射基本理论

物体热辐射原因在于构成物体的材料内部带电粒子的热运动，即处于非绝对零度状态的材料内部的电子和离子不断的进行热运动，从而在材料中形成极化电流源，这些电流源会产生电磁场 [11] 。由于极化电流源的电场和磁场不同分量的空间相关函数的平均值不为零，极化电流源的电磁场能够传播能量 [12] 。

在讨论两物体之间辐射传热之前，首先讨论单一物体表面的电磁场辐射，即求解以涨落电流为辐射源的麦克斯韦方程组。本节以面积无限大、厚度无限厚的平板上表面的热辐射情况为目标，在厚度方向上将平板分成很多层作为极化电流源层，再以一层极化电流源为对象，利用其统计特性和麦克斯韦方程研究一层极化电流源辐射电磁波在厚度方向上的传播，以及通过计算电磁波的坡印廷矢量得到在该电流源作用下平板表面向空间辐射的电磁能量。其中，主要关注的是在平板表面形成表面电磁波，这部分电磁波在极近距离物体表面间的隧穿是形成近场热辐射的原因 [3] 。

2.1. 涨落电流的统计特征

涨落耗散定理是联系不可逆过程中的能量耗散和平衡态热涨落的重要定理 [13] 。根据该定理，当物体处于热力学平衡(温度T)时，其内部由带电粒子热运动引起的极化电流密度的相关函数可以表示为 [10] [11] [12] [13] [14] ：

$\langle j_l\left({\stackrel{\to }{r}}^{\prime },\omega \right)j_n^{\ast }\left({\stackrel{\to }{r}}^{″},\omega \right)\rangle =\frac{1}{\text{π}}\omega {\epsilon }_0\mathrm{Im}\left({\epsilon }_r\right)\Theta \left(\omega ,T\right){\delta }_{ln}\delta \left({\stackrel{\to }{r}}^{\prime }-{\stackrel{\to }{r}}^{″}\right)$ (1)

式中，角括号代表系综平均，星号代表复共轭， $j_l\left({\stackrel{\to }{r}}^{\prime },\omega \right)$ 和 $j_n\left({\stackrel{\to }{r}}^{″},\omega \right)$ 分别是在位置 ${\stackrel{\to }{r}}^{\prime }$ 和 ${\stackrel{\to }{r}}^{″}$ 处波动电流密度的傅立叶分量， $\mathrm{Im}\left({\epsilon }_r\right)$ 是介质相对介电常数的虚部， $\Theta \left(\omega ,T\right)$ 是量子力学谐振子在频率为 $\omega$ 时的平均热能，它的表达式为：

$\Theta \left(\omega ,T\right)=\hslash \omega \left[\frac{1}{2}+\frac{1}{\exp \left(\hslash \omega /k_{B}T\right)-1}\right]$

其中， $2\text{π}\hslash$ 是普朗克常数， $k_B$ 是玻尔兹曼常数， ${\delta }_{ln}$ 是克罗内克德尔塔函数， $\delta \left({\stackrel{\to }{r}}^{\prime }-{\stackrel{\to }{r}}^{″}\right)$ 是狄拉克德尔塔函数。

2.2. 单层极化电流元辐射的电磁场

格林函数法是通过叠加同等边界条件点源产生的场来计算任意源生成的场。通常点结构源有x、y、z三个坐标，在仅研究点结构源的z坐标变化时，点结构源即变为单层结构源。因此，可以得到由单层极化电流源所产生的在任意位置 ${\stackrel{\to }{r}}^{\prime }$ 处的的“电型并矢格林函数”和“磁型并矢格林函数”分别为 [15] ：

$\begin{array}{c}{\stackrel{\leftrightarrow }{G}}^E\left(\stackrel{\to }{r},{\stackrel{\to }{r}}^{\prime }\right)=-\hat{z}\hat{z}\frac{\delta \left(z-z^{\prime }\right)}{k_m^2}+\frac{i}{2}{\displaystyle \iint \frac{\text{d}\stackrel{\to }{K}}{{\left(2\text{π}\right)}^2}}\frac{1}{k_{0z}}\left(\hat{s}\hat{s}+{\hat{p}}_{+}{\hat{p}}_{+}\right)\theta \left(z-z^{\prime }\right){\text{e}}^{i{k}_{0z}·z}{\text{e}}^{i\stackrel{\to }{K}\cdot \left(\stackrel{\to }{R}-{\stackrel{\to }{R}}^{\prime }\right)}\\ +\frac{i}{2}{\displaystyle \iint \frac{\text{d}\stackrel{\to }{K}}{{\left(2\text{π}\right)}^2}}\frac{1}{k_{0z}}\left(\hat{s}\hat{s}+{\hat{p}}_{-}{\hat{p}}_{-}\right)\theta \left(z^{\prime }-z\right){\text{e}}^{-i{k}_{0z}·z}{\text{e}}^{i\stackrel{\to }{K}\cdot \left(\stackrel{\to }{R}-{\stackrel{\to }{R}}^{\prime }\right)}\end{array}$ (2)

$\begin{array}{c}{\stackrel{\leftrightarrow }{G}}^H\left(\stackrel{\to }{r},{\stackrel{\to }{r}}^{\prime }\right)=\frac{i}{2}{\displaystyle \iint \frac{\text{d}\stackrel{\to }{K}}{{\left(2\text{π}\right)}^2}}\frac{k_{+}}{2k_{0z}}\left({\hat{p}}_{+}\hat{s}-\hat{s}{\hat{p}}_{+}\right)\theta \left(z-z^{\prime }\right){\text{e}}^{i{k}_{0z}\cdot z}{\text{e}}^{i\stackrel{\to }{K}\cdot \left(\stackrel{\to }{R}-{\stackrel{\to }{R}}^{\prime }\right)}\\ +\frac{i}{2}{\displaystyle \iint \frac{\text{d}\stackrel{\to }{K}}{{\left(2\text{π}\right)}^2}}\frac{k_{-}}{2k_{0z}}\left({\hat{p}}_{-}\hat{s}-\hat{s}{\hat{p}}_{-}\right)\theta \left(z^{\prime }-z\right){\text{e}}^{-i{k}_{0z}\cdot z}{\text{e}}^{i\stackrel{\to }{K}\cdot \left(\stackrel{\to }{R}-{\stackrel{\to }{R}}^{\prime }\right)}\end{array}$ (3)

式中，i为虚数， $\delta \left(z-z^{\prime }\right)$ 为狄拉克函数， $\theta \left(z-z^{\prime }\right)$ 为阶跃函数， $\stackrel{\to }{K}$ 为波矢量水平方向分量， $\hat{s}$ 为TE偏振波的偏振方向， $\hat{p}$ 为TM偏振波的偏振方向。

2.3. 平板表面辐射的电磁场

平板通过其表面向空间辐射电磁波实现辐射传热，这一过程可视为平板内部所有层极化电流源辐射电磁波通过界面的传播过程 [12] [13] [14] [15] [16] 。设定本文的平板是面积无限大、厚度无限厚的平板，在坐标系中的位置和材料分布情况为：平板的上表面设置在z轴源点( $z=0$ )，下表面在z轴无穷远处，即平板与自由空间的分界线位于z轴源点。平板内部记为材料2，自由空间记为材料1。并且，材料2中存在层极化电流源并且 $z=0^{-}$ 处的电磁场为材料2中该处以下所有层极化电流源辐射电磁场的叠加，材料1中不含热辐射源，其中的电磁场是材料2中电磁场经过界面传播得到。由此，用电型并矢格林函数和磁型并矢格林函数描述材料2中的层极化电流源与材料1中的电场和磁场的关系如下 [15] ：

${\stackrel{\leftrightarrow }{G}}^E\left(\stackrel{\to }{r}\right)={\displaystyle \iint \frac{\text{d}\stackrel{\to }{K}}{{\left(2\text{π}\right)}^2}}\frac{j}{2k_{z2}}\left(\hat{s}{t}_{21}^s\hat{s}+{\hat{p}}_{1+}{t}_{21}^s{\hat{p}}_{2+}\right){\text{e}}^{\left(i{k}_{z1}\cdot z_1-i{k}_{z2}\cdot z_2\right)}{\text{e}}^{i\stackrel{\to }{K}\cdot \stackrel{\to }{R}}$ (4)

${\stackrel{\leftrightarrow }{G}}^H\left(\stackrel{\to }{r}\right)={\displaystyle \iint \frac{\text{d}\stackrel{\to }{K}}{{\left(2\text{π}\right)}^2}}\frac{k_{1+}}{2k_{z2}}\left({\hat{p}}_{1+}{t}_{21}^s\hat{s}-\hat{s}{t}_{21}^s{\hat{p}}_{2+}\right){\text{e}}^{\left(i{k}_{z1}\cdot z_1-i{k}_{z2}\cdot z_2\right)}{\text{e}}^{i\stackrel{\to }{K}\cdot \stackrel{\to }{R}}$ (5)

式中， $t_{21}^s$ 为界面处电磁波的透射系数，该系数中包含了1和2两种材料的介电常数和折射率参数。

由于平板表面在单位时间内和单位面积上发射的某一频率电磁场携带的瞬时能量为电磁场坡印廷矢量的系综平均值，依据电磁场系综平均值的定义和公式(1)、(4)和(5)可以得到平板表面的辐射能量密度为：

$\begin{array}{c}{\langle \stackrel{\to }{S}\left(\stackrel{\to }{r},\omega \right)\rangle }_z=\frac{\omega \Theta \left(\omega ,T\right)}{4{\text{π}}^{2}c}{\displaystyle {\int }_0^{\infty }{\text{e}}^{2\mathrm{Im}\left(k_{z1}\right)z_1}\frac{\mathrm{Re}\left(k_{z1}\right)}{{\left|k_{z1}\right|}^2{k}_0}}[\mathrm{Re}\left(k_{z1}\right)\left(1-{\left|r_{21}^s\right|}^2\right)-2\mathrm{Im}\left(k_{z1}\right)\mathrm{Im}\left(r_{21}^s\right)\\ +\mathrm{Re}\left({\epsilon }_{r1}^{\ast }\right)\left(1-{\left|r_{21}^p\right|}^2\right)-2\mathrm{Im}\left({\epsilon }_{r1}^{\ast }{k}_{z1}\right)\mathrm{Im}\left(r_{21}^p\right)]K\text{d}K\end{array}$ (6)

式中， ${\epsilon }_{r1}^{\ast }$ 为材料1的相对介电常数的共轭， $r_{21}^s$ 和 $r_{21}^p$ 分别为界面对TE波和TM波的反射系数。

3. 平行的二氧化硅平板之间近场辐射传热

对于两物体间的辐射传热研究，常采用两个面积无限大、厚度无限厚的平板并且二者表面相互平行的结构作为模型。在这个模型下根据第1节的方法可以得到“电型并矢格林函数”和“磁型并矢格林函数”，以及由此得到的坡印廷矢量系综平均值。

3.1. 平行平板间的近场辐射传热

两个平板的表面之间均向对方辐射电磁波，在计算两者间的辐射传热时要计算两者辐射电磁波的能量差。不失一般性地，设定两个平板相互辐射电磁场的表面分别位于 $z=0$ 和 $z=d$ ，由此平板的间距为 $d$ 。由此，在两个平行平板之间由单一频率的电磁波引起的近场辐射热流密度为：

$q^{\omega }={\langle \stackrel{\to }{S}\left(\stackrel{\to }{r},\omega \right)\rangle }_{z^{0\to d}}-{\langle \stackrel{\to }{S}\left(\stackrel{\to }{r},\omega \right)\rangle }_{z^{d\to 0}}$ (7)

将式(7)对频率积分并简化，得到近场辐射传热模型为：

$q=\frac{1}{4{\text{π}}^2{d}^2}{\displaystyle \int \left[\Theta \left(\omega ,T_2\right)-\Theta \left(\omega ,T_1\right)\right]}\frac{\mathrm{Im}\left({\epsilon }_{r1}\right)}{{\left|{\epsilon }_{r1}+1\right|}^2}\frac{\mathrm{Im}\left({\epsilon }_{r2}\right)}{{\left|{\epsilon }_{r2}+1\right|}^2}\text{d}\omega$ (8)

其中， $T_1$ 和 $T_2$ 分别是两块平板各自的温度， $d$ 为两块平板的距离，即辐射距离。

从近场辐射传热模型可以看到，当两块平行平板间存在辐射传热时，近场辐射传热与辐射距离 $d$ 成平方反比关系。

3.2. 二氧化硅材料的介电特性

近场辐射传热是两物体在极近距离下其表面电磁波隧穿的结果，而物体表面是否形成表面电磁波与构成该物体的材料特性有关，具体地，材料的相对介电常数的实部小于−1 [17] 。

二氧化硅相对介电常数与频率有关，两者的关系可以用Lorentz振子模型描述 [18] 。利用二氧化硅的介电常数模型计算得到频率为 $0.9\times {10}^{14}\text{rad}/\text{s}$ 和 $2.0\times {10}^{14}\text{rad}/\text{s}$ 时介电常数的数值为−3.9和−6.5，这两个值均小于−1。因此，在二氧化硅表面存在表面电磁波，当两个二氧化硅物体距离足够近时能够发生近场热辐射现象。

将二氧化硅的相对介电常数带入式(8)中，即得到平行的二氧化硅平板间的近场辐射模型。由于该模型中的平板面积无限大、厚度无限厚，基于该模型可以得到二氧化硅物体间近场辐射传热的上限。

4. 近场热辐射传感器的辐射距离参数设定

4.1. 近场辐射传热系数

定义辐射传热系数 $h$ 研究辐射温度T和辐射距离 $d$ 对近场热辐射的影响并建立模型，具体为：

$h=\underset{\Delta T\to 0}{\lim }\frac{q}{\Delta T}$ (9)

由此，依据式(7)和(8)计算得到两种近场辐射传热系数，一种是对应单一频率电磁波作用的辐射传热系数 $h^{\omega }$ ，另一种是涵盖所有频率电磁波作用的辐射传热系数 $h$ ，具体如下：

$h^{\omega }=\frac{1}{4{\text{π}}^2{d}^2}\frac{\mathrm{Im}\left({\epsilon }_{r1}\left(\omega \right)\right)}{{\left|{\epsilon }_{r1}\left(\omega \right)+1\right|}^2}\frac{\mathrm{Im}\left({\epsilon }_{r2}\left(\omega \right)\right)}{{\left|{\epsilon }_{r2}\left(\omega \right)+1\right|}^2}\times k_{B}T{\left(\frac{\hslash \omega }{k_{B}T}\right)}^2\frac{\exp \left(\hslash \omega /k_{B}T\right)}{{\left(\exp \left(\hslash \omega /k_{B}T\right)-1\right)}^2}$ (10)

$h={\displaystyle {\int }_0^{\infty }\frac{1}{4{\text{π}}^2{d}^2}\frac{\mathrm{Im}\left({\epsilon }_{r1}\left(\omega \right)\right)}{{\left|{\epsilon }_{r1}\left(\omega \right)+1\right|}^2}\frac{\mathrm{Im}\left({\epsilon }_{r2}\left(\omega \right)\right)}{{\left|{\epsilon }_{r2}\left(\omega \right)+1\right|}^2}}\times k_{B}T{\left(\frac{\hslash \omega }{k_{B}T}\right)}^2\frac{\exp \left(\hslash \omega /k_{B}T\right)}{{\left(\exp \left(\hslash \omega /k_{B}T\right)-1\right)}^2}\text{d}\omega$ (11)

式(10)为针对单一频率电磁波作用的近场辐射传热模型，式(11)为全部电磁波作用的近场辐射传热模型，该模型与文献中的模型一致 [14] [19] 。

4.2. 仿真确定辐射距离参数

利用式(11)完成如下仿真计算：参数T从1 K升高到700 K，参数 $d$ 分别为1000 nm、800 nm、700 nm、600 nm、500 nm、400 nm和300 nm，计算结果如图1所示。图中还给出了黑体辐射传热系数 $h_{\text{bk}}$ 和远场热辐射传热系数 $h_{\text{fr}}$ 对应计算值，这两个系数是依据式(9)和经典辐射传热理论得到。图1中水平坐标为温度，单位为K，垂直坐标为辐射传热系数，单位为W∙m⁻²∙K⁻¹，图中交点1至4分别是 $d$ 为1000 nm、800 nm、700 nm和600 nm时 $h$ 曲线与 $h_{\text{fr}}$ 曲线的交点，坐标分别为(313，2.465)、(474，8.565)、(554，13.686)、(647，21.781)；交点5至7分别是 $d$ 为600 nm、500 nm和400 nm时 $h$ 曲线与 $h_{\text{bk}}$ 曲线的交点，坐标分别为(304，6.381)、(443，19.775)、(578，43.921)。上述数据表明 $d$ 为1000 nm时近场辐射传热能力与远场辐射传热能力相当， $d$ 为600 nm近场辐射能力与黑体辐射能力相同，并且随着 $d$ 减小近场辐射迅速增强，并均大于黑体辐射。依据此仿真结果可以确定所需测量近场辐射传热的距离，即传感器结构中的近场辐射传热距离，这是设计近场辐射传感器的关键参数。

5. 实验方案及近场热辐射传感器

5.1. 实验方案及对应的传感器结构

辐射传热对于辐射源和吸收体来说产生的效果是不同的，可制定两种测量方案和对应的近场热辐射传感器。

方案1：如图2所示，对于辐射源，由于辐射传热导致能量散失，其自身的温度会下降。为了保持辐射源的温度(T_e)不变，需要给辐射源提供更多的电功率，即 ${\left(i_1-i_2\right)}^{2}R$ (R为加热单元的电阻值)，通过测量电流的变化可测得近场辐射传热。

方案2：如图3所示，对于吸收体，由于通过辐射传热吸收了能量，其自身的温度会增加，在无近场辐射传热情况下通过对吸收体输入加热电流能达到同等的温度(T_a)，输入电流形成的热功率为 $i_1^{2}R$ (R为加热单元的电阻值)，通过测量加热电流能实现近场辐射传热的测量。

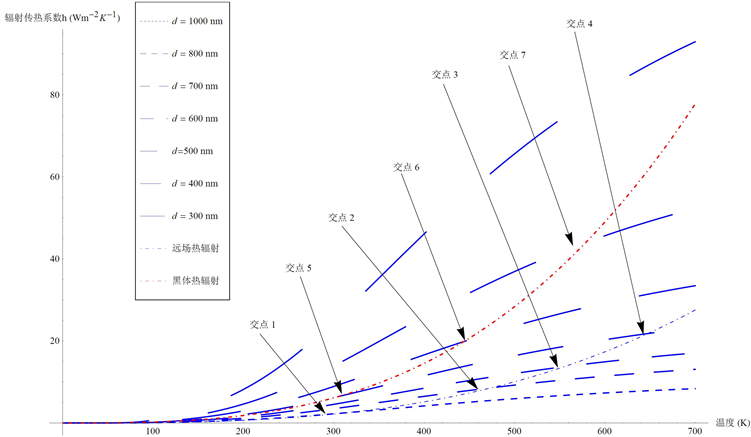
Figure 1. Data: the character of near-field thermal radiative heat transfer

图1. 近场辐射传热特性数据

(a) (b)

Figure 2. Experimenta plan l and its NFTR sensor. (a) having no near-field thermal radiation, (b) having near-field thermal radiation

图2. 实验方案1及对应的近场热辐射传感器。(a) 无近场热辐射的情况，(b) 存在近场热辐射的情况

依据前述近场辐射传热测量方案可以设计两种形式的传感器：

1) 传感器形式一

如图2(b)所示的近场热辐射传感器包括辐射源结构和吸收体结构。并且，辐射源结构中有加热单元和测温单元，用于维持加热单元的温度；吸收体应与环境温度保持一致并通过测温单元检测。

2) 传感器形式二

如图3(a)所示近场热辐射传感器包括辐射源结构和吸收体结构。并且，辐射源结构与和吸收体结构中均有加热单元和测温单元。要求吸收体应具备良好的绝热性，能将近场辐射传热转变为明显的温度变化。

(a)(b)

Figure 3. Experimenta plan 2 and its NFTR sensor. (a) having no near-field thermal radiation, (b) having near-field thermal radiation

图3. 实验方案2及对应的近场热辐射传感器。(a) 无近场热辐射的情况，(b) 存在近场热辐射的情况

5.2. 近场热辐射传感器的实验模型

在经典辐射传热理论文献中将具有不同几何特征的物体间的辐射传热归结为不同的类型分别建立模型，包括平行平板的辐射传热模型、球体和平板的辐射传热模型以及两个同心圆桶的辐射传热模型等 [1] 。其中，平行平板辐射传热模型具有如下特征：1) 发生辐射传热的两个物体均为平板；2) 平板之间的垂直距离处处相等。该模型的一种理想形式是当平板的长度和宽度大于平板间距10倍以上时视角系数为1，即可认为离开一个平板的能量全部到达另一平板，这时可不考虑两平板边缘的辐射传热。

若图2(b)和图3(a)所示的近场热辐射传感器结构以平行平板辐射传热模型为实验模型，在设计中应保证如下条件：第一、辐射源结构表面与吸收体结构表面均为平板结构；第二、辐射源结构和吸收体结构相互平行，即二者表面的间距处处相同；第三、辐射源结构和吸收体结构的长度和宽度都超过二者间距10倍以上。

5.3. 近场热辐射传感器的微加工工艺

微米纳米量级悬空二氧化硅(SiO₂)薄膜结构具有热响应快、功耗低等优点，已经成为研制微、纳米器件的一种常见结构，包括风速计、皮拉尼真空传感器、非制冷式红外传感器和微型加热器等 [20] [21] [22] 。在这些微型传感器的结构单元中涵盖了加热单元和测温单元，相关工艺可以用于近场热辐射传感器的加工。不同之处在于：近场热辐射传感器中需要制作两块悬空二氧化硅薄膜的结构，并且薄膜中分别制作加热单元和测温单元作为热辐射的辐射源和吸收体。

此外，近场辐射传热发生在微米或纳米距离下的物体之间，构造两个间距为微米或纳米级的两个悬空薄膜结构是实现近场辐射传热实验测量的必需，也是设计和制作近场热辐射传感器的重点和难点。实现薄膜结构悬空的常用的加工技术是“表面微加工”工艺和“正面体硅微加工”工艺是目前常用技术 [23] [24] 。文献15中给出了具体工艺流程。

6. 面向其他材料的近场热辐射实验测量

6.1. 近场热辐射的频谱特性

利用式(10)仿真计算二氧化硅材料的近场热辐射的电磁波波谱特征，如图4所示。在400 nm、500 nm、

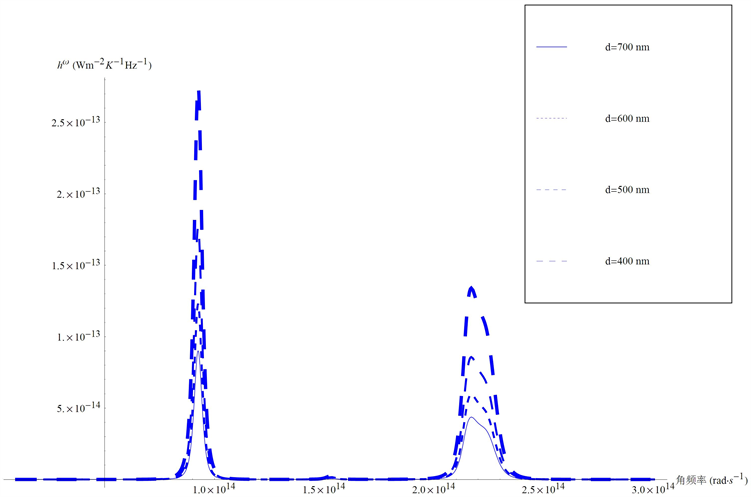
Figure 4. Data: The spectral characteristics of near field thermal radiative heat transfer between two SiO₂ plates

图4. 近场辐射传热频谱特性数据

600 nm和700 nm辐射距离下电磁波隧穿现象发生在频率 $0.9\times {10}^{14}\text{rad}/\text{s}$ 和 $2.0\times {10}^{14}\text{rad}/\text{s}$ 处，并且辐射距离越小电磁波的隧穿现象也显著。

不同材料物体间的电磁波隧穿的频率和距离都不相同，因此，要以此为依据设计传感器中辐射源与吸收体的距离。具体地，可将相应材料的介电常数替换式(10)和式(11)中的介电常数 ${\epsilon }_{r2}^{\ast }$ ，从而得到其他材料的近场辐射传热系数，从而确定近场热辐射传感器的关键参数。文献18中给出了多种材料的介电常数实验测试数据。

6.2. 制作不同种类近场热辐射传感器

对于其他介质材料表面间的近场辐射传热测量的传感器而言，在结构设计上可参考图2(b)和图3(a)中的结构，不同之处在于传感器结构中的二氧化硅换成其他材料，如碳化硅等，并用相关的材料制备工艺加工。

7. 结论

本文以二氧化硅材料为例给出了利用微型传感器测量近场辐射传热的基本方法。该方法涵盖了传感器结构参数设计、实验方案确定、传感器加工等步骤。基于本论文方法的实验已经发表论文 [10] [15] [25] ，其可行性得到了部分研究者的认可 [26] 。在此基础上，本文提出了基于该方法实验测量其他介质材料物体间的近场辐射传热的拓展，具体方法是：1) 在近场热辐射理论仿真计算中用待测材料的介电常数替换本文中二氧化硅的介电常数；2) 在制作近场热辐射传感器时，将传感器辐射源和吸收体中的二氧化硅换成待测材料。

基金项目

国家自然科学基金重大项目(60806038)，国家自然科学基金项目(61131004)，国家自然科学基金项目 (61503058)，大连民族大学博士启动基金(110074)，大连民族大学自主基金项目(DC201501057)。