浅谈配电线路差动保护方案设计

Design of Differential Protection Scheme for Distribution Lines

摘要: 配电线路的安全运行是保证电力系统安全运行的重要条件，当配电线路发生故障时，快速、准确地切断和隔离故障线路并保持非故障线路的持续运行既是保证供电可靠性的要求，也是提高电力系统安全稳定运行必不可少的前提条件。基于基尔霍夫定律的电流差动保护无论对于何种形式的配电线路都是一种简单、可靠、选择性强的保护形式。首先，本文对目前线路保护的研究和实际应用情况进行了讨论和分析，比较了常用线路差动保护的实现原理和实现条件及优缺点。其次，针对常规相量电流差动保护易受正常负荷电流和故障过渡电阻影响的缺点，同时为加快差动保护的动作速度，本文将相间工频变化量差动保护与采样值差动保护结合起来，提出了一种基于相电流采样值变化量相间差的小电流接地保护的新方法，并对此保护方法的原理、判据、动作特性等作了讨论和分析。

Abstract: The safe operation of distribution line is an important condition to ensure the safe operation of power system. when the distribution line fails, cutting off and isolating the fault lines quickly and accurately and keeping the continuous operation of the Fei line is not only the requirement of en-suring the reliability of power supply, but also the essential prerequisite to improve the safe and stable operation of the power system. The current differential protection based on the kirchhoff law is a simple, reliable and selective protection form for any form of distribution line. First of all, this paper discusses and analyzes the current research and practical application of line protection, and compares the realization principle and realization condition, advantages and disadvantages of common line differential protection. Secondly, according to the conventional phase current diffe-rential protection is vulnerable to normal load current and fault transient resistance, at the same time, in order to speed up the movement speed of differential protection, this paper combines the alternating current differential protection with sampling value differential protection, proposes a new method of small current grounding protection based on the phase current sampling value change, and discusses and analyzes the principle, criterion and action characteristics of this pro-tection method.

1. 引言

对于电力系统继电保护来说，电流差动保护是一种最为理想的保护形式，它具有灵敏度高、简单可靠、动作速度快等优点，目前已经被广泛地应用于电力系统的发电机、变压器、母线等电力系统电气设备的保护中，电流差动保护之所以是最为理想的保形式，从继电保护的观点来说是因为差动电流完全消除了非故障状态下的电流影响，因此在各种非正常但又没有发生故障的电力系统运行状态下，它能够可靠不动作，例如能够适应系统振荡及线路的非全相运行等各种非正常运行状态，同时又能够准确反应各种故障，由于它不需要测量电压量，因此不受TV断线影响的特点 [1] 。

目前的线路保护中，基于距离测量和相位比较原理构成的保护，当应用于多端和多回线路中都有各种缺陷，在多端线路中某个线路连接点之后发生故障时，从前面线路看进去的阻抗(距离)会受另一条线路电流的影响，因此距离无法准确测量，而电流差动保护对此类线路具有良好拓扑适应能力和天然的选相能力，并能够很好地解决目前并架双回线和多端线路中保护配置困难以及短距离线路保护中整定困难等问题，这对提高电力系统稳定性和提高输配电系统的运行灵活性有着重要的意义 [2] 。

传统的相量电流差动保护虽然有着不少的优点，但它同样也有缺点，如保护的灵敏度会受负荷电流和接地故障过渡电阻的影响，随着电力市场环境的变化和大联网电力系统的逐渐形成，传统的相量电流差动保护在动作速度上有时也满足不了要求，需要采用新型的电流差动保护来实现故障的判断，以提高保护动作的速度。

为加快保护动作速度，需采用新的保护原理，基于瞬时采样值电流差动保护的动作速度比较快，它是根据电流瞬时采样值进行保护判断的，当连续R个采样值中有S个采样值满足制动方程时则保护出口动作，为了达到和相量电流差动保护同样的效果，利用瞬时采样值的电流差动保护理论上只需要四分之一周期的数据窗时间就能判断是否发生保护区内故障，不过瞬时采样值电流差动保护在动作区域上有模糊区，因此需要辅助判据，当电流瞬时采样值处于瞬时采样值电流差动保护的模糊区域时，由辅助判据来判定是否线路发生保护区内故障。

故障时的配电网络可以认为是由正常运行时的网络和附加的故障分量网络所叠加而成的，利用故障电流分量构成差动保护可以消除负荷电流和接地过渡电阻对电流差动保护的影响，但是故障分量一般只在故障后的一个周期内有效，因此故障分量保护只在保护启动后一个周期内投入，如果一个周期内没有动作则投入传统的全电流相量差动保护 [3] 。

2. 配电线路常规相量电流差动保护

电流差动保护原理建立在基尔霍夫电流定律的基础之上，把被保护的电气设备看成是一个节点，那么正常时流进被保护设备的电流和流出的电流相等，差动电流等于零。当设备出现故障时，流进被保护设备的电流和流出的电流不相等，差动电流大于零。当差动电流大于差动保护装置的整定值时，保护动作，将被保护设备的各侧断路器跳开，使故障设备断开电源。电流差动保护又称为“平衡保护”，它的基本原理是在上世纪初提出的，迄今为止，已约有100年的历史。其具有原理简单，良好的选择性，简单可靠、灵敏度高、动作速度快的特点，已广泛应用到电力系统线路和发电机、变压器、母线等作为主保护之一。然而应用对象的不同，对电流差动保护原理的要求也不同。本节内容主要是介绍线路的电流差动保护基本原理 [4] 。

线路纵联差动保护已经成为线路保护的主要保护之一，其工作原理是基于比较被保护线路始端和末端电流的大小和相位。在线路两端安装了具有型号相同和电流比一致的电流互感器，它们的二次绕组用电缆连接起来，其连接方式应使正常运行或外部短路故障时继电器中没有电流，而在被保护线路内部发生故障时，其电流等于短路点的短路电流。如图1为环流法接线的纵差保护单相原理接线图，图中，将线路两端电流互感器二次侧带“·”号的同极性端子连接在一起，将不带“·”号的同极性端子连接在一起，差动继电器接在差流回路上。

当线路MN正常运行和被保护线路外部(k2点)短路时，按规定的电流正方向看，M侧电流为正，N侧电流为负，两侧电流大小相等、方向相反， ${\displaystyle \sum \stackrel{\dot{}}{I}}={\stackrel{\dot{}}{I}}_M+{\stackrel{\dot{}}{I}}_N=0$ ，反应在电流互感器二次回路中流过差动继电器中的电流为故障点总的短路电流的二次值，即

${\stackrel{\dot{}}{I}}_r={\stackrel{\dot{}}{I}}_m+{\stackrel{\dot{}}{I}}_n=\frac{1}{K_{TA}}\left({\stackrel{\dot{}}{I}}_M+{\stackrel{\dot{}}{I}}_N\right)=0$ (1)

当线路内部短路(k1点)时，流经配电线两侧的故障电流均为正方向，且 ${\displaystyle \sum \stackrel{\dot{}}{I}}={\stackrel{\dot{}}{I}}_M+{\stackrel{\dot{}}{I}}_N={\stackrel{\dot{}}{I}}_{k1}$ ，反映在电流互感器二次侧流入到差动继电器中的电流为故障点总的短路电流的二次值，即

${\stackrel{\dot{}}{I}}_r={\stackrel{\dot{}}{I}}_m+{\stackrel{\dot{}}{I}}_n=\frac{1}{K_{TA}}\left({\stackrel{\dot{}}{I}}_M+{\stackrel{\dot{}}{I}}_N\right)=\frac{{\stackrel{\dot{}}{I}}_{k1}}{K_{TA}}$ (2)

Figure 1. Short circuit schematic diagram of a current longitudinal differential protection area

图1. 电流纵联差动保护区外、区内短路示意图

当流入继电器的电流 ${\stackrel{\dot{}}{I}}_r$ 大于继电器整定的动作电流 $I_{op,r}$ 时，差动保护继电器动作。

由以上分析看出，纵差保护范围为线路两端TA之间的距离，在保护范围外短路，保护不动作，故不需要与相邻元件在保护动作值和动作时限上配合，因此可以实现瞬时切除故障。

3. 电流采样值接地保护方法原理

配电线路的电流差动保护已经从模拟式保护发展到利用微处理器和数字通信的全数字式保护，而电流瞬时采样值的电流差动保护近年来已经成为数字式电流差动保护的理想方案。

3.1. 采样值电流差动保护与常规电流差动保护的关系

常规的电流差动保护中差动量和制动量的求取一般是反应电流的有效值或平均值等，通过滤波等办法消除非周期分量和谐波分量的影响。在计算机继电保护的有效值计算方法中，故障时引起的非周期分量和谐波分量尽管衰减很快，但可能在较长时间内影响计算的准确性，即采用时间窗为一个周期的算法，若开始几个采样值中含较高的非基波分量，则将影响与这些采样值相关的各个周期的计算结果。如果要保证保护动作的可靠性，势必影响保护的动作速度。若电流差动保护的动作判据按每一个采样值分别判断，则可以在原理上完全消除这种影响，有效地提高电流差动保护的动作速度与可靠性 [5] 。

常规相量差动通过计算动作量和制动量的有效值或平均值构成差动保护判据，因而在稳态过程中，保护制动特性不会因为采样数据窗的移动而发生改变。但这种基于相量的差动保护也存在着如下不足：

1) 在遇到很大的干扰脉冲而出现个别坏数据时，其有效值或平均值会很大，易造成保护的误动；

2) CT饱和也是造成常规相量差动保护不正确的动作原因之一，当引入差动回路的CT出现严重饱和时，将产生较大的差流有效值，在一定条件下就可能引起差动保护误动；

3) 基于相量的差动保护，其计算相量需要一定的数据窗，导致在一个周波后才能发出跳闸指令，这对于严重内部故障，动作时间略显不够快。

采样值差动保护对每一个时刻的采样值进行差动判别，在连续R次判别中如有S次满足判据，则输出动作信号。在遇到一个甚至几个坏数据时，只要坏数据的个数小于S，保护均不会误判。从CT特性看，即使CT饱和比较严重，在过零点附近也会有一段线性传变区，只要合理地选择S、R值，就可保证外部故障时满足动作判据的点数不足S点。因此，采样值差动保护动作的可靠性将高于有效值差动保护。此外，采样值差动保护最快动作时间为故障后的S个采样点发跳闸指令，S的取值小于一个周波采样点数，所以其动作速度一般快于常规相量差动保护。

目前采样值差动保护正逐步引起广泛重视，并开始将其应用于短配电线和变压器保护的实际工程，为此有必要对其动作特性作系统的研究。本文对影响采样值差动保护动作特性的几个关键问题进行深入的理论研究。

3.2. 瞬时采样值电流差动保护制动方程

瞬时采样值电流差动保护的制动方程和相量电流差动保护的制动方程类似，例如两端线路的制动方程 [6] 可以如下：

$i_d>I_0$ (3)

$i_d>K\times i_T$ (4)

其中： $i_1$ ， $i_2$ 为线路两端的电流采样瞬时值。

$i_d=\left|i_1+i_2\right|$ 为动作电流， $i_T=\left|i_1-i_2\right|$ 为制动电流。

K为制动系数， $i_0$ 为整定值(是一常数)。

瞬时采样值是随时间的变化而呈现周期性变化的，因此差动电流、不平衡电流、制动电流也都是随时间的变化而周期性变化的，瞬时采样值电流差动保护的制动方程对不同的采样点制动效果是不一样的，有一些采用点的制动效果比较好，而有一些采样点的制动效果比较差。

采样值差动保护对每一个时刻的采样值进行差动判别，在采用连续的R个采样点中，若有S个采样点满足就动作的判据(R一般比S大2)，则输出动作信号。在遇到一个甚至几个坏数据时，只要坏数据的个数小于S，保护均不会误判。此外，采样值差动保护最快动作时间为故障后的S个采样点发跳闸指令，S的取值小于一个周波采样点数，故其动作速度一般快于常规相量差动保护。

3.3. R和S的选取

为保证动作判据的正确性，通常采用重复多次判别方法，即连续R次采样判别中有S次及以上符合动作判据，则输出动作信号。基于这种考虑，有必要分析R，S值的选取。

从确保采样值差动保护的制动性能不低于常规相量差动保护的角度分析得出，判别数据窗对应的角度θ必须满足θ ≥ 90˚，即采样值差动S的选取必须满足：

$S=\frac{90}{360}\times N+1=0.25N+1$ (5)

式中：N——每周波采样点数。

对应于采样率12点/周期，需满足S ≥ 4。S值根据式(5)来取，而R取值要比S值大，其选取需重点考虑以下两个因素：

内部故障时，采样值差动数据窗可能遇上过零点，导致采样值差动判据不满足。考虑极端情况，当过零点位于两采样值中点时，有可能使连续两采样点不满足差动判据，故一般需取R ≥ S + 2，但R值也不能取过大，不能大于N/2，取值过大会影响保护的动作速度。

为保证采样值差动判据的可靠性，即内部故障时正确动作，外部故障时不误动，R-S值不宜过大，同时当S确定后，R值过大也减小了动作速度。

以上仅从保证可靠性的角度来考虑R值的选取。实际应用中，可根据不同的用途调整R、S的取值。需要强调的是，尽管R、S的选取对不同使用目的有不同方法，但在具体应用中发现，R-S值取为2在可靠性和灵敏度的综合评估中要优于其它取法(对12点/周期而言)。采样值差动保护中R的选取应满足R-S ≥ 2。

3.4. 采样值电流差动保护的动作模糊区

由于电流数据的采样值是离散化的，即使电流处于稳态，在不同时刻电流的采样值也是不同的，而且采样初始时刻不同，即采样点位置的不同，也会产生不同的采样序列，不同采样序列的采样值大小也是不同的，从而使得刚好有S个点满足动作判据的动作电流幅值也可能会不同，即刚好满足动作判据的动作电流幅值不确定，这就是采样值电流差动保护动作值模糊区产生的原因。

与常规相量差动保护不同，采样值差动的动作需靠重复性判别来实现，又由于采样值的离散性，使得采样值差动在动作电流大小的确定上存在一个模糊区。具体来说就是存在一个区间 $\left[\alpha ,\beta \right]$ ，当工频电流有效值满足 $I>\beta$ 时，采样值差动能可靠动作，当 $I<\alpha$ 时，采样值差动能保证不误动，但当 $\alpha \le I\le \beta$ 时，采样值差动却处于临界状态，可能动作也可能不动作，具体要根据工频电流的相位而定 [7] 。

3.5. 采样值电流差动保护的动作速度

使用采样值电流差动保护的重要原因之一是试图提高电流差动保护的动作速度。从上面的分析知道，保护在一个与半个周期左右动作出口，对采样值电流差动保护来说，性能没有多少区别，而由于动作边界存在不确定部分，过分提高采样值电流差动保护的动作速度则是不现实的。同时，在分析中采样值电流差动保护与传统电流差动保护制动效果相当的假设条件是，必须在半个周期中有 > 90˚的角度范围满足动作判别方程 [8] 。因此，尽管通过提高电流差动保护的采样速度，可大大减少采样值电流差动保护动作边界的变化范围，但是，采样值电流差动保护出口动作速度无论如何必须 > 5 ms(对于频率为50 Hz的电网来说即对应于90˚)，才能保证采样值电流差动保护的可靠性。

4. 仿真结果

本文的仿真将采用EMTP建模并产生一些较原始的数据导入MATLAB程序中进行数据的进一步计算和图形的生成。以一个35 kV配电网为例进行仿真分析，如图2。

其母线上带有L1，L2，L3，L4四条馈线：L1为架空线路，L2为多回馈线集中等效线路，L3为电缆线路，L4为架空线路。整个系统的对地分布分布电容为418。考虑馈线的分支、非线性负荷和单相负荷的影响，分析馈线4发生单相(C相)接地故障的情况 [9] [10] 。

根据中性点接地方式、补偿度、故障接地方式以及故障电阻等的不同情况，分别进行实验测试。其中中性点接地方式包括不接地、谐振接地(v = 0)、经消弧线圈过补偿接地(v = −10%)、经消弧线圈欠补偿接地(v = 10%)、高阻接地(R0 = 400 Ω)四种方式。故障接地类型包括金属性接地(Rf = 5 Ω)和高阻接地(Rf = 2000 Ω)两种类型。

4.1. 中性点不接地方式结果

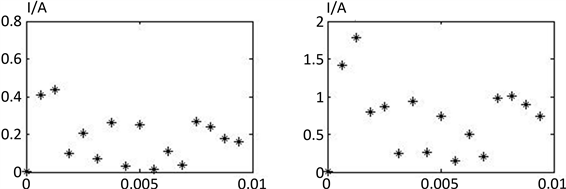
由图3(a)可见，非故障线路L1的电流采样值变化量相间差最大值小于0.04 A，即id0 = 0.04 A，该数值是因为装置的测量误差和故障干扰信号所致。由图3(b)可见，非故障线路L3的电流采样值变化量相间差最大值较线路L1稍大一些，但小于2A，即id0 = 2A。由图3(c)可见，非故障线路L1的电流采样值变化量相间差最大值较线路L1、L2也稍大一些，但小于5A，即id0 = 5A。这是因为线路L3比在三条非故障线路中离故障线路L4最近，受故障影响也最大。由图3(d)可见，故障线路4大部分采样点(11点)的电流采样值变化量相间差大于10 A。按2 kΩ高阻接地故障保护灵敏动作的要求，选择保护整定值为5A，则故障线路L4能灵敏动作，非故障线路L1、L2、L3均能可靠不误动。

由图4(a)可见，非故障线路L1的电流采样值变化量相间差最大值小于0.04 A，即id0 = 0.04 A，该数值是因为装置的测量误差和故障干扰信号所致。由图4(b)可见，非故障线路L1的电流采样值变化量相间差最大值较线路L1稍大一些，但小于0.2A，即id0 = 0.2A。由图4(c)可见，非故障线路L3的电流采

Figure 2. Simulation circuit diagram

图2. 仿真电路图

(a) 线路L1最大相间差值 (b) 线路L2最大相间差值(c) 线路L3最大相间差值 (d) 线路L4最大相间差值

Figure 3. Neutral point ungrounded, The interphase difference of the variation of the current sampling value at a metal failure (Rf = 5 Ω)

图3. 中性点不接地、金属性故障(Rf = 5 Ω)时电流采样值变化量的相间差值

Figure 4. Neutral point ungrounded, The interphase difference of the variation of the sampled value of the current in a nonmetallic fault (Rf = 2000 Ω)

图4. 中性点不接地、非金属性故障(Rf = 2000 Ω)时电流采样值变化量的相间差值

样值变化量相间差最大小于0.15A，即id0 = 5A。由图4(d)可见，故障线路4大部分采样点(12点)的电流采样值变化量相间差大于5 A。按2 kΩ高阻接地故障保护灵敏动作的要求，选择保护整定值为5A，则故障线路L4能灵敏动作，非故障线路L1、L2、L3均能可靠不误动。

4.2. 中性点经消弧线圈接地方式结果

根据图3及图4相同的分析原理，从图5~图10可以得出，当中性点经消弧线圈直接接地时，按2 kΩ高阻接地故障保护灵敏动作的要求，选择保护整定值为5A，则故障线路L4能灵敏动作，非故障线路L1、L2、L3均能可靠不误动。

(a) 线路L1最大相间差值 (b) 线路L2最大相间差值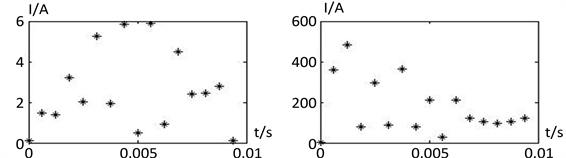(c) 线路L3最大相间差值 (d) 线路L4最大相间差值

Figure 5. Neutral point via arc suppression coil (v = 0%)、Metal grounding fault (Rf = 5 Ω) The interphase difference of the change of the current sampling value

图5. 中性点经消弧线圈(v = 0%)、金属性接地故障(Rf = 5 Ω)时电流采样值变化量的相间差值

(a) 线路L1最大相间差值 (b) 线路L2最大相间差值(c) 线路L3最大相间差值 (d) 线路L4最大相间差值

Figure 6. Neutral point via arc suppression coil (v = 0%)、Metal grounding fault (Rf = 2000 Ω) The interphase difference of the change of the current sampling value

图6. 中性点经消弧线圈(v = 0%)、非金属性接地故障(Rf = 2000 Ω)时电流采样值变化量的相间差值

(a) 线路L1最大相间差值 (b) 线路L2最大相间差值(c) 线路L3最大相间差值 (d) 线路L4最大相间差值

Figure 7. Neutral point via arc suppression coil (v=-10%), Metal grounding fault (Rf = 5 Ω) The interphase difference of the change of the current sampling value

图7. 中性点经消弧线圈(v = −10%)、金属性接地故障(Rf = 5 Ω)时电流采样值变化量的相间差值

(a) 线路L1最大相间差值 (b) 线路L2最大相间差值(c) 线路L3最大相间差值 (d) 线路L4最大相间差值

Figure 8. Neutral point via arc suppression coil (v = −10%), Metal grounding fault (Rf = 2000 Ω)The interphase difference of the change of the current sampling value

图8. 中性点经消弧线圈(v = −10%)、非金属性接地故障(Rf = 2000 Ω)时采样值变化量的相间差值

4.3. 中性点经高阻接地方式结果

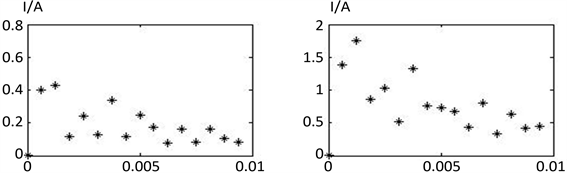
根据图3及图4相同的分析原理，从图11及图12可以得出，当中性点经高阻(R0 = 400 Ω)接地时，按2 kΩ高阻接地故障保护灵敏动作的要求，选择保护整定值为5A，则故障线路L4能灵敏动作，非故障线

(a) 线路L1最大相间差值 (b) 线路L2最大相间差值(c) 线路L3最大相间差值 (d) 线路L4最大相间差值

Figure 9. Neutral point via arc suppression coil (v = 10%), Metal grounding fault (Rf = 5 Ω) The interphase difference of the change of the current sampling value

图9. 中性点经消弧线圈(v = 10%)、金属性接地故障(Rf = 5 Ω)时电流采样值变化量的相间差值

(a) 线路L1最大相间差值 (b) 线路L2最大相间差值(c) 线路L3最大相间差值 (d) 线路L4最大相间差值

Figure 10. Neutral point via arc suppression coil (v = 10%), Metal grounding fault (Rf = 2000 Ω)The interphase difference of the change of the current sampling value

图10. 中性点经消弧线圈(v = 10%)、非金属性接地故障(Rf = 2000 Ω)时采样值变化量的相间差值

路L1、L2、L3均能可靠不误动。

本文提出了基于电流采样值相间差的配电网接地保护原理和方法，构建了接地保护判据。该保护方法直接采用微处理器CPU的AD采样数据进行计算，无需滤波处理，采样信号中包括了高频信号，利用

(a) 线路L1最大相间差值 (b) 线路L2最大相间差值(c) 线路L3最大相间差值 (d) 线路L4最大相间差值

Figure 11. Neutral point high resistance ground (R0 = 400 Ω), Metal grounding fault (Rf = 5 Ω) The interphase difference of the change of the current sampling value

图11. 中性点高阻接地(R0 = 400 Ω)、金属性接地故障(Rf = 5 Ω)时电流采样值变化量的相间差值

(a) 线路L1最大相间差值 (b) 线路L2最大相间差值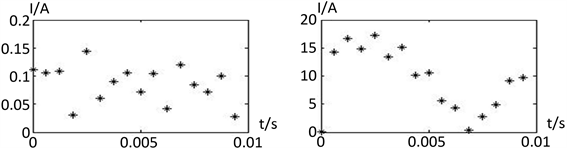(c) 线路L3最大相间差值 (d) 线路L4最大相间差值

Figure 12. Neutral point high resistance ground (R0 = 400 Ω), Nonmetallic grounding fault (Rf = 2000 Ω) The interphase difference of the change of the current sampling value

图12. 中性点高阻接地(R0 = 400 Ω)、非金属性接地故障(Rf = 2000 Ω)时电流采样值变化量的相间差值

弧光故障暂态分量，能有效地提高保护的抗弧光故障能力。应用EMTP仿真软件建立了小电流接地系统的仿真模型，通过对中性点消弧线圈、接地电阻等参数设置不同值来对故障选线新方法的选线效果进行分析证明该保护方法可以保护具有2 kΩ故障电阻的高阻故障，具有较高的保护精度和可靠性，且只需测量被保护线路的电压、电流，便于在FTU上安装，实现线路的分段就地保护，满足配电自动化的要求。

5. 结语

对常规相量电流差动保护基本原理进行简单的介绍，将瞬时采样值差动保护与常规相量电流差动保护进行了比较。并对瞬时采样值差动保护常用判据作了分析，研究了影响保护性能的相关因素，得出以下结论：

1) 对于每周采样12点的采样值电流差动保护来说，在半个周期内满足保护动作判据的判断次数不宜小于4次(即保证在> 90˚的角度范围内满足动作判据)，6取4的保护方案是可行的。

2) 在计算机继电保护的软、硬件条件许可下，提高数据采样率对采样值电流差动保护性能提高十分有利。提高采样率可以减少采样值电流差动保护动作边界的变化区域，同时当保护动作出口速度不变时，提高采样率将有助于改善采样值电流差动保护的可靠性。但应注意的是，不能因为采样率提高而将保护动作速度无限制地提高，原理上采样率与动作速度没有直接关系，采样值电流差动保护的出口速度极限为5 ms (对频率为50 Hz的电网而言)。

3) 如果采样值电流差动保护能保证其制动效果与常规电流差动保护的制动效果相当，那么其整定方法容易从使用相同原理判据的常规电流差动保护的整定方法中类比过来，抗电流互感器饱和的方法亦可采用常规电流差动保护中使用的同类方法 [11] 。