1. 引言
在供应链中,每个成员是独立的利益主体,决策的目标是追求各自利益最大化,这往往与供应链系统的目标冲突,导致供应链整体的效益低下、服务水平下降。因此,供应链管理的重要工作是通过协调和控制成员之间的生产活动,实现降低成本,提高利润和服务水平。
供应链契约是指通过提供合适的信息和激励措施,保证买卖双方协调、优化销售渠道绩效的有关条款,常用的契约有收益共享契约,回购契约,回馈与惩罚契约等。然而,由于实际生产的复杂性,往往需要两种形式的契约联合起来才能实现供应链协调,例如:徐琪 [1] 研究了用回购和价格弹性联合契约协调供应链的问题,Adhikari [2] 等在时尚服装供应链中,设计了回购与收益共享联合契约,并分析了契约参数对供应链的影响。Xiao [3] 等研究了资金约束的供应链,发现回购与收益共享的联合契约可以协调供应链。Taylor [4] 等研究了市场需求受努力水平影响的供应链,发现回购与回馈惩罚契约的联合,能够协调供应链。He [5] 等进一步研究了市场需求受价格及努力水平影响的供应链,发现回购契约和回馈与惩罚契约均不能协调供应链,但两者的联合契约可以实现供应链的协调;而Hematyar [6] 等在此基础增加了顾客的订货行为,发现回购和回馈与惩罚的联合契约可以实现供应链的协调。在已有的供应链协调研究成果中,大多数是基于决策者完全理性的分析框架下,以利润最大化为决策目标,忽视了决策者的行为特征。
实际上,决策者不仅期望获得最大的利润,还注重在心理活动下实现预期目标的可能性 [7] 。常见的心理活动有:风险规避、过度自信、公平关切等。目前,已经有一些学者在研究供应链协调时将决策者的心里活动作为重要的影响因素。刘云志 [8] 等研究了风险规避供应商的供应链协调问题;石岿然 [9] 等研究了零售商具有过度自信行为的供应链;姚锋敏 [10] 等建立了公平关切下零售商主导的供应链决策及协调模型。上述研究的特点是将决策者的心理活动作用在利润函数上,并以反映决策者偏好的效用函数作为决策目标。
由于现实环境和生产的复杂性,决策者需要考虑多方面的因素,决策的目标也不是单一的。最近,Yao [11] 等研究了一类零售商考虑下游风险的供应链协调问题,其中下游风险指实际利润不超过决策者目标利润的概率,实际上是指零售商的决策目标是将风险控制在预期范围内追求利润最优。本文试图研究一类零售商允许有限损失的供应链协调问题,与文 [11] 不同,零售商的决策目标是在期望损失不超过允许值的条件下,最大化自己的利润。首先,建立了期望损失在允许范围内的优化期望利润的模型,给出最优解的解析表达式;然后,引入回购契约来减少零售商的损失,使得期望损失在允许值内,最后分别引入收益共享契约和回馈与惩罚契约来协调供应链,并通过数值例子来说明模型的可行性。
2. 问题描述
在由一个供应商和一个零售商组成的二级供应链中,零售商以单位价格
(
)向供应商订购产品(订购量为
),并以单位价格
(
)出售给顾客。假设市场对产品的需求
为非负的随机变量,均值为
,其密度函数和分布函数分别为
和
。供应商按照零售商的订单组织生产,单位生产成本为
。
由于需求的不确定性,零售商会产生超储或缺货损失,即若订购产品超过市场需求(
),则零售商的单位超储损失为
;若市场需求超过订购量(
),则零售商的单位缺货损失(机会损失)为
。零售商的损失函数为
根据文 [12] 得到:使零售商期望损失
最小的订购量
及其最小期望损失值
分别为
(1)
本文研究一个允许有限损失的零售商和一个供应商组成的供应链的协调问题。假设零售商是允许有限损失的,即要求损失在允许范围内,即
(2)
其中:
是参数且
,
称为损失允许值;零售商也是理性,尽可能追求利润最优。因此,零售商的决策目标是在满足条件(2)下使其期望利润最大。
关于零售商允许有限损失的供应链协调的定义如下:
定义1如果一个契约能够使得下列条件成立:
1) 由缺货或超储引起的零售商的损失在允许值范围内;
2) 分散式供应链系统的期望利润等于集中式供应链的最优期望利润;
3) 供应商和零售商的期望利润不小于批发价契约下的期望利润,
则称该契约实现了零售商允许有限损失的供应链的协调,简称供应链协调。
3. 集中式供应链
供应链系统的期望利润为
. (3)
引理1 [13] 使供应链系统期望利润
最大的生产量
及其最大期望利润
分别为
. (4)
4. 批发价契约下的分散式供应链
4.1. 零售商以期望利润最大化为目标的决策
零售商的期望利润函数为
(5)
引理2 [13] 使零售商期望利润
最大的订购量
及其最大期望利润
分别为
.(6)
供应商的期望利润函数为
(7)
显然,
,因此,零售商不可能同时实现利润最大和损失最小。
4.2. 零售商以损失在允许范围内利润最大为目标的决策
由于市场环境的复杂,零售商从自身利益出发,当发现订购任何数量的产品,对自身不利时,零售商将不订购产品,即订购量为0,下面假设零订购时,零售商面对的损失也在允许范围内,即
,此时
。
在批发价契约下,允许有限损失的零售商的决策问题为
(8)
定理1 记问题(8)的最优解为
,则
(9)
其中,
为满足约束条件
最大的订购量,即方程
(10)
的唯一解。
证明:对
关于Q求二阶导数得:
,显然,
,故
是关于Q的严格凹函数。由引理2可知
为最大值点,故
在
单调递增,在
单调递减。
同理可证,
是关于Q的严格凸函数,由
可知,存在唯一
,使得
,且 时,
时,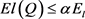 恒成立。若
恒成立。若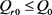 ,则
,则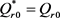 ;否则,由
;否则,由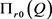 的单调性可知,
的单调性可知, 。
。
显然,由于损失约束的限制,当 时,零售商不能用最优订购量
时,零售商不能用最优订购量 订货,这对零售商是不利的;而当
订货,这对零售商是不利的;而当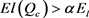 时,零售商不能用最优订购量
时,零售商不能用最优订购量 订货,这将影响供应链系统的绩效。因此,为了实现供应链协调,供应链成员必须采取措施,使零售商增加订购量且损失在允许范围内,才能使供应链系统的绩效得到优化。
订货,这将影响供应链系统的绩效。因此,为了实现供应链协调,供应链成员必须采取措施,使零售商增加订购量且损失在允许范围内,才能使供应链系统的绩效得到优化。
5. 回购与收益共享契约下的供应链
在此情形下,供应商以单位价格 回购零售商未售出的产品,降低了零售商的损失,使得零售商能够采用最优订购量
回购零售商未售出的产品,降低了零售商的损失,使得零售商能够采用最优订购量 订货,作为回报供应商将分享零售商的销售收益,分享比例为
订货,作为回报供应商将分享零售商的销售收益,分享比例为 。
。
5.1. 零售商的决策
零售商的期望利润为
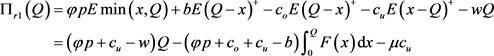 (11)
(11)
而零售商的期望损失为
 (12)
(12)
允许有限损失的零售商的决策问题为
 (13)
(13)
显然, ,当
,当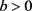 时,
时, 且
且 是b的减函数,所以,当
是b的减函数,所以,当 时,可以选择适当的b使得
时,可以选择适当的b使得 。
。
为求问题(13)的解,首先求对给定的b,使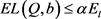 成立的Q的范围。
成立的Q的范围。
由于 ,
,
当 时,
时, 是Q的减函数。由
是Q的减函数。由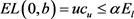 可知,对所有的
可知,对所有的 均满足
均满足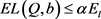 。
。
当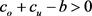 时,
时, 是Q凸函数,由
是Q凸函数,由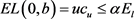 可知,存在唯一
可知,存在唯一 ,使得
,使得 时,满足
时,满足 ,其中
,其中 是方程
是方程
 (14)
(14)
的解。
定理2记问题(13)的最优解为 ,当
,当 且
且 时,
时,
1) 若 ,则
,则 ;
;
2) 若 ,则
,则 ,
,
其中
 (15)
(15)
证明:对 关于Q分别求一阶和二阶导数得:
关于Q分别求一阶和二阶导数得:
 ,
,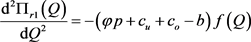 ,
,
由 及
及 可知,
可知, ,因此,
,因此,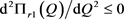 ,即
,即 为Q的凹函数。
为Q的凹函数。
由 可知,
可知, ,
,
由 可知,
可知, 。
。
故存在 ,使得
,使得 ,整理即得(15)式,由
,整理即得(15)式,由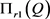 的凹性可知,
的凹性可知, 为最大值点,且
为最大值点,且 在
在 上单调递增,在
上单调递增,在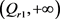 上单调递减。
上单调递减。
当 时,
时, ,故
,故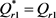 。
。
当 时,若
时,若 ,则
,则 ;否则,由
;否则,由 的单调性可知,
的单调性可知, 。
。
供应商的期望利润函数为
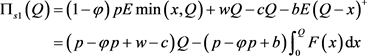 (16)
(16)
5.2. 协调问题
定理3若回购和收益共享契约的参数 满足:
满足:
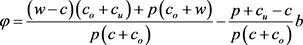 (17)
(17)
且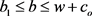 ,分散式供应链的期望利润等于集中式供应链的最优期望利润,且零售商的损失在允许范围内,其中
,分散式供应链的期望利润等于集中式供应链的最优期望利润,且零售商的损失在允许范围内,其中
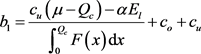 . (18)
. (18)
证明:由 及(17)式可知:
及(17)式可知: ,要使零售商及供应链协调同时为最优,必须
,要使零售商及供应链协调同时为最优,必须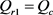 ,即
,即

整理即得(17)式。
当 时,利用(12)式得到
时,利用(12)式得到
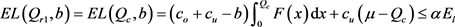 ,
,
于是,当 且(17)成立时,若零售商的订购量为
且(17)成立时,若零售商的订购量为 ,则
,则 ,且
,且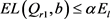 ,即零售商的期望损失在允许范围内,且分散式供应链系统的期望利润等于集中式供应链系统的期望利润。
,即零售商的期望损失在允许范围内,且分散式供应链系统的期望利润等于集中式供应链系统的期望利润。
若要使供应链协调,还应满足:
 (19)
(19)
定理4若契约参数 满足(17)式,且
满足(17)式,且 ,则供应链可以协调,其中
,则供应链可以协调,其中
 ,
, , (20)
, (20)
 ,
, ,
, 。
。
证明:由 可知,
可知, ,且
,且 ;由
;由 可知,
可知, ,且
,且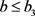 。
。
当 及
及 满足(17)式时,结合定理3可知,定义1中的条件(i)(ii)成立。
满足(17)式时,结合定理3可知,定义1中的条件(i)(ii)成立。
由式(11)及式(17)整理得: ,由
,由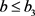 可得:
可得: ;
;
同理,由式(16)及式(17)整理得: ,由
,由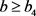 可得:
可得: 。
。
因此,当 时,(19)式成立,即定义1中的条件3i)成立。
时,(19)式成立,即定义1中的条件3i)成立。
综上,回购与收益共享契约参数满足式(17)及 时,定义1中的1) 2) 3)三个条件均满足,则供应链可以协调。
时,定义1中的1) 2) 3)三个条件均满足,则供应链可以协调。
5.3. 数值算例
假设市场需求 服从
服从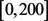 的均匀分布,模型中用到的各参数如下:
的均匀分布,模型中用到的各参数如下: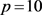 ,
, ,
,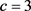 ,
, ,
,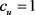 ,
, 。由(1)可得:
。由(1)可得: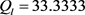 ,
, ,此时,最大允许损失值为:
,此时,最大允许损失值为: ,由(9)式可得:
,由(9)式可得: ,零售商和供应商的期望利润分别为
,零售商和供应商的期望利润分别为 ,
, ,由式(4)可得:
,由式(4)可得: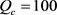 ,故
,故 。
。
当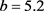 时,由(17)式得:
时,由(17)式得: ,由(15)式及(4)式可得:
,由(15)式及(4)式可得: ,此时零售商的期望损失
,此时零售商的期望损失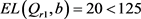 。从图1可以看出,收益共享和回购契约下零售商以及供应链系统的期望利润在
。从图1可以看出,收益共享和回购契约下零售商以及供应链系统的期望利润在 时,同时达到最优。
时,同时达到最优。
由(20)式可得: ,
, ,在
,在 内以0.1250为间隔对
内以0.1250为间隔对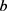 进行取值,由(17)式计算出
进行取值,由(17)式计算出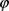 ,并计算出零售商的期望损失(
,并计算出零售商的期望损失( )、零售商的期望利润(
)、零售商的期望利润( )和供应商的期望利润(
)和供应商的期望利润( ),结果如下表所示。
),结果如下表所示。
由表1可知,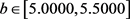 时,零售商的期望损失
时,零售商的期望损失 、
、 且
且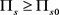 ,由定义1可知,供应链协调。此外,由表1可以看出,随着
,由定义1可知,供应链协调。此外,由表1可以看出,随着 的逐渐增大,收益共享比例
的逐渐增大,收益共享比例 逐渐减小,零售商的期望损失逐渐减小且在允许范围内,供应商分担了零售商更多的损失,使得零售商能够按照最优订货量
逐渐减小,零售商的期望损失逐渐减小且在允许范围内,供应商分担了零售商更多的损失,使得零售商能够按照最优订货量 订货,实现了对零售商的订货激励,并保证了整个供应链系统的期望利润最大。
订货,实现了对零售商的订货激励,并保证了整个供应链系统的期望利润最大。
6. 回购与回馈惩罚下的供应链
在此情形下,供应商设定销售目标 ,对于零售商超额完成的部分单位奖励为
,对于零售商超额完成的部分单位奖励为 (
(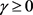 ),未完成的
),未完成的

Figure 1. Expected profit curve of retailer and supply chain system under buyback-revenue-sharing contract
图1. 回购与收益共享契约下零售商和供应链系统的期望利润曲线

Table 1. The impact of on, and the expectations of the retailers and suppliers
表1. 对
对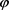 ,
,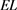 以及零售商和供应商期望利润的影响
以及零售商和供应商期望利润的影响
部分单位惩罚也为 ,同时以单位价格
,同时以单位价格 回购零售商未售出的产品。
回购零售商未售出的产品。
6.1. 零售商的决策
零售商的期望利润为
 . (21)
. (21)
其期望损失函数与(12)式相同。
允许有限损失的零售商的决策问题为
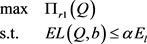 (22)
(22)
定理5记问题(22)的最优解为 ,当
,当 时,
时,
1) 若 ,则
,则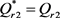 ;
;
2) 若 ,则
,则
其中
 ; (23)
; (23)
 由(14)式确定。
由(14)式确定。
证明:对 分别求一阶、二阶导数得:
分别求一阶、二阶导数得:
 ,
, ,
,
显然,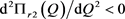 ,即
,即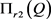 为
为 的严格减函数。
的严格减函数。
又
 ,
, ,
,
由介值定理可知,存在 使得
使得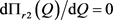 ,整理即得(23)式。
,整理即得(23)式。
由 可知,
可知, 为唯一的最大值点,且
为唯一的最大值点,且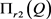 在
在 上单调递增,在
上单调递增,在 上单调递减。
上单调递减。
当 时,
时, ,故
,故 。
。
当 时,若
时,若 ,则
,则 ;否则,由
;否则,由 的单调性可知,
的单调性可知, 。
。
供应商的期望利润函数为:
 . (24)
. (24)
6.2. 协调问题
定理6如果回购与回馈惩罚契约参数 满足
满足

且: 时,分散式供应链的期望利润等于集中式供应链的最优期望利润,且零售商的期望损失在允许范围内。
时,分散式供应链的期望利润等于集中式供应链的最优期望利润,且零售商的期望损失在允许范围内。
证明:要使零售商及供应链系统同时达到最优,必须 ,即
,即

整理即得(25)式。
当 时,利用(12)式得:
时,利用(12)式得: 。
。
于是当 且(25)式成立时,若零售商的订购量为
且(25)式成立时,若零售商的订购量为 ,则
,则 ,且
,且 ,即零售商的期望损失在允许范围内,且分散式供应链系统的期望利润等于集中式供应链系统的期望利润。
,即零售商的期望损失在允许范围内,且分散式供应链系统的期望利润等于集中式供应链系统的期望利润。
要使供应链协调,还应满足下面条件:
 (26)
(26)
定理7若契约参数 满足:
满足:
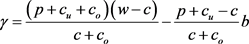 (27)
(27)
且 ,则供应链协调,其中
,则供应链协调,其中
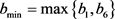 ,
, , (28)
, (28)
 ,
, ,
, ,
,
 .
.
证明:由 知:
知: ,
, ;由
;由 知:
知: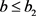 ,
,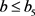 ,
, 。
。
当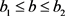 ,若契约参数
,若契约参数 满足(27)式,结合定理6可知,分散式供应链系统的期望利润和集中式供应链的最优期望利润相等,且零售商的损失在允许范围内。此时满足定义1中的条件1) 2)。
满足(27)式,结合定理6可知,分散式供应链系统的期望利润和集中式供应链的最优期望利润相等,且零售商的损失在允许范围内。此时满足定义1中的条件1) 2)。
当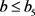 时,由(27)式可得:
时,由(27)式可得: 。
。
由(21)式及(27)式整理得:
 ,
,
由 可得:
可得: 。
。
由(24)式及(27)式整理得:

由 可得:
可得: 。
。
综上,当 及(27)式成立,定义1中的条件3)成立。
及(27)式成立,定义1中的条件3)成立。
结合定理4及定理5可知:回购和回馈惩罚契约参数满足式(25)及 时,定义1中的1) 2) 3)三个条件均满足,则供应链可以协调。
时,定义1中的1) 2) 3)三个条件均满足,则供应链可以协调。
6.3. 数值算例
取 ,其它参数取值同5.3.
,其它参数取值同5.3.
取 ,由(27)式计算得
,由(27)式计算得 ,此时零售商的期望损失
,此时零售商的期望损失 ,从图2可以看出,零售商以及供应链系统的期望利润在
,从图2可以看出,零售商以及供应链系统的期望利润在 处均达到最优。
处均达到最优。
由(28)式得: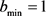 ,
, ,下面将
,下面将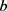 在区间
在区间 上以0.1250为间隔进行取值,讨论供应链的协调性,由此可得表2。
上以0.1250为间隔进行取值,讨论供应链的协调性,由此可得表2。
由表2可知,当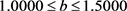 时,零售商的期望损失小于允许值,且零售商和供应商的期望利润均不低于批发价格契约下的期望利润,由定义1可知,供应链实现了协调,且随着
时,零售商的期望损失小于允许值,且零售商和供应商的期望利润均不低于批发价格契约下的期望利润,由定义1可知,供应链实现了协调,且随着 的增加,奖励惩
的增加,奖励惩

Figure 2. Expected profit curve of retailer and supply chain system under buyback-rebate-penalty contract
图2. 回购与回馈惩罚契约下零售商和供应链系统的期望利润曲线

Table 2. The impact of on, and the expectations of the retailers and suppliers
表2. 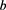 对
对 、零售商的期望损失以及零售商和供应商期望利润的影响
、零售商的期望损失以及零售商和供应商期望利润的影响
罚因子 逐渐减少,零售商的期望损失逐渐减少,当
逐渐减少,零售商的期望损失逐渐减少,当 为0.8750时,虽然零售商和供应商的期望利润高于批发价格下的期望利润,但零售商的期望损失超过允许值.
为0.8750时,虽然零售商和供应商的期望利润高于批发价格下的期望利润,但零售商的期望损失超过允许值.
7. 小结
本文研究了零售商允许有限损失的供应链协调问题。结果表明:当契约参数满足给定的条件且在一定范围时,回购与收益共享联合契约、回购与回馈惩罚联合契约可以实现供应链的协调。本文的研究工作丰富了供应链协调理论,对具有损失厌恶的零售商的供应链管理决策具有一定的指导作用。
基金项目
国家自然科学基金项目(71261002)。