基于模拟–优化模式的梯级水库群突发水污染事件应急调度研究

Emergency Dispatching for Cascade Reservoirs of Sudden Water Pollution Accidents Based on the Model of Simulation and Optimization

摘要: 根据突发水污染事件特征及相关影响因素，在水动力模型、水质模型的基础上，建立了基于模拟–优化模式的梯级水库群突发水污染事件应急调度优化模型。以清江中下游为例，采用改进的NSGA-II算法，对水布垭–隔河岩–高坝洲梯级水库群应急调度优化模型的决策变量(应急调度函数中的控制变量)进行多目标优化，得到了Pareto最优解集及相应的Pareto前沿，并探讨了水库群联合调度在应对突发性水污染事件的合理性与有效性。结果表明，在水位、库容允许的情况下，优先调用距离污染源较近的或与被污染河段直接相连的水库，启动应急调度最多可使污染物浓度达标时间减少80.4%。根据优化结果分析了应急调度过程中损失的电能与污染物达标所用时间之间的竞争关系，并定量模拟了突发水污染事件中污染物浓度的沿程变化与随时间变化的过程。

Abstract: According to characteristics and influences of sudden water pollution accidents, an emergency optimal operation model of simulation and optimization was established for cascade reservoirs based on hydrodynamic model and water quality model. The middle and lower reaches of Qingjiang River are selected as the case study. Applying a multi-objective optimization on the decision variables of the model (the control variables of emergency operating rules of QingJiang cascade reservoirs) by using improved NSGA-II algorithm results in the Pareto solutions and Pareto fronts and then the feasibility and effectiveness of emergency dispatching are discussed. The analysis results show that, the reservoirs close to the pollution source or directly connected with the polluted river should be called first in the capacity of reservoir storage. The time of reaching standard can be reduced by up to 80.4% when taking emergency dispatching. According to the optimization results, the competition between the energy lost in the emergency dispatch process and the time reaching standard is analyzed. The distribution of pollutant concentrations and the process of pollutant concentration changes with time are quantitatively simulated.

1. 引言

近年来，随着各类水库水电站的建成和投入使用，我国的水电工程事业已经进入了从建设到水库群联合优化调度的关键转型期 [1] 。由于不可控因素及各种随机因素的影响，水库群水污染重大突发事故时有发生。1994年带有流域性的淮河大面积污染灾害，其直接经济损失达1.7亿元 [2] 。水库群重大突发性事故不仅使得水库的工程效益得不到正常的发挥，而且可能严重污染水源，直接威胁人民群众的身体健康，甚至影响下游基础设施和生态与环境安全 [3] 。

关于水库的突发水污染事件应急调度问题，国内外已展开了一些研究。利用数学模型模拟污染物迁移扩散已成为主流方法 [4] [5] 。王庆改等 [6] 基于MIKE11模型定量模拟了2003年水文条件下不同情况的突发性水污染事件中污染物运移扩散过程。在文献 [7] [8] 中，作者分析了突发水污染事件的污染源，利用贝叶斯网格模型计算了水污染事件的风险，并对不同情境下的突发水污染进行了应急处置。练继建等 [9] 建立了水库突发水污染事件风险评价指标体系，并以丹江口水库为例进行了应用分析。辛小康等 [10] 通过三峡水库分析了不同调度方式对突发水污染事件的污染物影响时间及污染物浓度的作用。王浩等 [11] 、丁洪亮等 [12] 也对突发水污染事故的应急调度提出了建设性的意见。

目前，虽然已经建立了一些能考虑梯级水库群应急优化调度的模型，但相关研究主要采用拟定多组方案进行模拟、优选的方法 [13] ，利用优化算法对梯级水库群进行应急调度仍然处于初级阶段。所以，研究如何通过水库群联合应急调度，既能达到保证人民群众生命安全的目标，又能尽量降低水污染所造成的损失，具有重大意义。鉴于此，本文以Python为编程语言，以马斯京根流量演算方程与连续方程为水动力模型、以一维对流扩散方程为水质模型，在此基础上建立了针对清江中下游的应急调度计算模型，对突发水污染事件进行动态模拟，根据损失的电能、污染物达标所用时间两项指标，采用改进的NSGA-II算法优选应急调度方案，从而得到一组最优解集。根据优化结果，分析了不同应急调度方案的收益与代价，由此给出应急调度的高效益方案集，并模拟了不同地点处污染物到达的时间和浓度值，对突发性水污染事件的梯级水库群应急调度有一定的指导意义。

2. 模型建立

综合考虑资料条件、模拟精度、计算效率等因素，水动力模型采用马斯京根流量演算方程和连续方程，水质方程采用一维对流扩散方程，建立了耦合水动力与水质模型的应急调度计算模型，对河流流量、横截面积、污染物浓度进行模拟计算。在此基础上，考虑应急调度的约束，建立了应对突发水污染事件的应急调度优化模型，从而对应急调度计算模型中水库群的调度函数进行多目标优化。

2.1. 水动力模型

2.1.1. 马斯京根流量演算方程

采用马斯京根分段连续演算的一般方法对河流流量进行模拟计算，结合连续方程模拟计算清江中下游各个断面处河流的流量和横截面积，作为后续水质模型计算的基础。将演算河段分为n个等长的子河段，相应的参数为 $K_l$ (蓄量常数)、 $x_l$ (槽蓄系数)，时段为 $\Delta t$ ，河段数用 $i$ 表示， $i=1,\cdots ,n$ ，时段数用 $j$ 表示， $j=1,\cdots ,m$ ， $m$ 为总时段数。则流量演算方程式为：

$Q_{ij}=C_0^i\cdot I_j^i+C_1^i\cdot I_{j-1}^i+C_2^i\cdot Q_{j-1}^i$ (1)

式中： $C_0^i=\frac{0.5\cdot \Delta t-K_l\cdot x_l}{0.5\cdot \Delta t+K_l-K_l\cdot x_l}$ ； $C_1^i=\frac{0.5\cdot \Delta t+K_l\cdot x_l}{0.5\cdot \Delta t+K_l-K_l\cdot x_l}$ ； $C_2^i=\frac{-0.5\cdot \Delta t+K_l-K_l\cdot x_l}{0.5\cdot \Delta t+K_l-K_l\cdot x_l}$ 。

2.1.2. 连续方程

考虑有旁侧入流时的连续方程为：

$\frac{\partial A}{\partial t}+\frac{\partial Q}{\partial x}=q$ (2)

式中：为河流断面面积；为河流纵向距离；Q为通过河流断面的流量；q为区间入流；为时间。

利用整体爬坡遗传算法对马斯京根模型的参数进行率定，然后联解式(1)、(2)，可求得河段的流量Q、断面面积等沿时间和流程的变化，这为水质模型的求解奠定了基础 [8] 。

2.2. 水质模型

对于河流来说，其长度要远远大于其深度和宽度，且在突发性水污染事故中，由于污染物浓度非常大，在较短的时间内，排入河流中的污染物较多。因此，本文将河流水质模型简化为一维水质问题，即，假定污染物排入河流中以后，在很短的距离内即在断面上混合均匀，并且只沿流程方向变化。一维污染物对流扩散方程为：

$\frac{\partial \left(CA\right)}{\partial t}+\frac{\partial \left(CQ\right)}{\partial x}=E\cdot \frac{\partial }{\partial x}\left(A\cdot \frac{\partial C}{\partial x}\right)-K_1\cdot C$ (3)

式中： $C$ 为河段中污染物的浓度； $E$ 为河段水流的综合扩散系数； $K_1$ 为水体污染物一级反应动力学降解系数。

由于式(3)是一个二阶、变系数抛物线型偏微分方程，采用特征有限差分法对其进行求解。

2.3. 应急调度优化模型

2.3.1. 目标函数

梯级水库群应急调度主要是通过各个水库加大出库流量来实现污染物的稀释和迁移扩散，同时也会因破坏水库原有运行方式而对发电不利，因此考虑污染物达标所用时间与应急调度过程中损失的电能，采用目标函数如下：

$\min t_{\text{end}}$ (4)

$\min E_{\text{waste}}={\displaystyle \underset{s=1}{\overset{n}{\sum }}{E}_{\text{extral-ideal}}^{\left(s\right)}}-{\displaystyle \underset{s=1}{\overset{n}{\sum }}{E}_{\text{extral-actual}}^{\left(s\right)}}$ (5)

式中： $t_{\text{end}}$ 为污染物达标所用时间； $E_{\text{waste}}$ 为应急调度过程中损失的电能； $n$ 为参与应急调度的水库个数； $E_{\text{extral-actual}}^{\left(s\right)}$ 为应急调度过程中消耗水库库容而产生的发电量； $E_{\text{extral-ideal}}^{\left(s\right)}$ 为理想情况下，消耗相同库容而产生的发电量。

2.3.2. 调度函数

梯级水库群突发水污染应急调度本质上是水库群出库流量的分配问题，考虑到起调时间、调度时长、调度流量等因素，假定水库在应急阶段的调度图如图1所示。从 $t_1^{\left(s\right)}$ 时刻开始以线性速度增大水库的出库流量，经过一段时间后到达 $Q_m^{\left(s\right)}$ ，然后保持一段时间 $t_{last}^{\left(s\right)}$ 后，再以同样的速度减少水库的出库流量至出库流量的初始值。水库s的调度轨迹由初始时刻 $t_1^{\left(s\right)}$ 、持续时间 $t_{last}^{\left(s\right)}$ 、应急调度最大出库流量 $Q_m^{\left(s\right)}$ 三个控制变量决定。

2.3.3. 约束条件

1) 污染物浓度达标约束：

$C\left(x,t\right)\le C_s\left(x\in x_p\right)$ (6)

式中： $C\left(x,t\right)$ 为河流中t时段位置x处污染物的浓度； $C_s$ 为符合水质目标的污染物浓度标准限制； $x_p$ 为城市取水口区域等保护河段。

2) s水库的水量平衡约束：

$V_s\left(t\right)=V_s\left(t-1\right)+\left[{\bar{I}}_s\left(t\right)-{\bar{Q}}_s\left(t\right)\right]\cdot \Delta t$ (7)

式中： $V_s\left(t-1\right)$ 、 $V_s\left(t\right)$ 分别为s水库t时段初、末的蓄水容积； ${\bar{I}}_s\left(t\right)$ 为第t时段水库平均入库流量； ${\bar{Q}}_s\left(t\right)$ 为第t时段水库平均出库流量。

3) s水库的库容曲线约束：

Figure 1. Graph of reservoir operation

图1. 水库调度图

$Z_{s,sy}\left(t\right)=f_{ZV}\left[V_s\left(t\right)\right]$ (8)

式中： $Z_{s,sy}\left(t\right)$ 为s水库t时段末上游水位； $f_{ZV}(\ast )$ 表示库容曲线函数。

4) s水库的库水位约束：

$Z_{s,sy}^{\min }\le Z_{s,sy}\left(t\right)\le Z_{s,sy}^{\max }$ (9)

式中： $Z_{s,sy}^{\min }$ 、 $Z_{s,sy}^{\max }$ 分别为s水库上游允许最低、最高水位。

5) s水库的下游水位流量关系约束：

$Z_{s,xy}\left(t\right)=f_{ZQ}\left[Q_{s,ck}\left(t\right)\right]$ (10)

式中： $Z_{s,xy}\left(t\right)$ 为s水库t时段末下游水位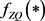；表示下游水位流量关系函数； $Q_{s,ck}\left(t\right)$ 为s水库t时段末的出库流量。

6) 水电站水头约束：

$\{\begin{array}{l}{H}_s^{\min }\le {\bar{H}}_s\left(t\right)\le H_s^{\max }\\ {\bar{H}}_s\left(t\right)=\frac{Z_{s,sy}\left(t-1\right)+Z_{s,sy}\left(t\right)}{2}-\frac{Z_{s,xy}\left(t-1\right)+Z_{s,xy}\left(t\right)}{2}-\Delta H_s\left(t\right)\\ \Delta H_s\left(t\right)=f_{\Delta H,s}\left[Q_{s,fd}\left(t\right)\right]\end{array}$ (11)

式中： ${\bar{H}}_s\left(t\right)$ 、 $\Delta H_s\left(t\right)$ 分别为t时段机组的平均水头和水头损失； $H_s^{\min }$ 、 $H_s^{\max }$ 分别为s水电站的最小和最大水头； $Q_{s,fd}\left(t\right)$ 为s水库t时段的发电流量； $f_{\Delta H,s}(\ast )$ 表示s水电站的水头损失函数。

7) 水电站出力约束：

$P_s^{\min }\le P_s\left(t\right)\le P_s^{\max }$ (12)

式中： $P_s^{\min }$ 、 $P_s^{\max }$ 分别为s水电站的最小、最大出力。

2.4. 模型求解及程序实现

应急调度模型是基于模拟–优化模式而建立，作为一个双目标优化模型，选用改进的NSGA-II算法进行求解。NSGA-II算法是带精英策略的非支配排序的遗传算法，为更好地搜索可行域的边界，对NSGA-II算法做了少许改进。按照改进后的NSGA-II算法对梯级水库群应急调度优化模型进行种群初始化，其中水库群调度轨迹的控制变量为优化变量，经过进化迭代计算可得到相应Pareto最优解集及Pareto前沿。每一个Pareto最优解对应着一个应急调度方案，通过模拟–优化模式，可以得到一个应急调度方案集合。

3. 实例研究

清江是长江中游在湖北省境内的第二大支流，全长423公里，全流域可开发装机容量为329万千瓦，相应年电能为105亿千瓦时。清江干流恩施市以下河段分三级开发，自上而下依次为水布垭、隔河岩、高坝洲三座水电站。选择水布垭–隔河岩–高坝洲梯级水库群作为研究案例，由 [8] [9] 可知突发水污染事件的污染源有相当一部分来源于交通事故，假定在高坝洲水库下游5 km处岳宜高速发生化工液体运输车翻车事故，10 t苯酚倒入清江形成瞬时点源污染，其中降解系数为2/d，综合扩散系数为50 m²⁄s，污染物浓度标准采用III类水质标准。

3.1. 水动力模型的率定与验证

对于水动力模型，采用渔峡口、长阳站在1984年6月份的实时流量数据进行参数率定，将1984年7~9月份数据进行验证。结果显示，模拟的流量与实测值非常吻合，率定期的纳什系数为0.98，检验期为0.96。整体来说，水动力模型符合要求，可以作为后续水质模型的基础。

3.2. 结果分析

利用改进的NSGA-II算法，可得到Pareto最优解集及相应Pareto前沿(图2)，显然图2的Pareto前沿上每一个点对应着一个调度方案。

为便于分析，在所求Pareto最优解集中选取六个有代表性的Pareto最优解进行分析，具体数据信息见表1。

通过表1的数据分析，方案F是遭遇突发水污染事件时未启动应急调度的数据信息，所选典型方案中达标时间最短则是方案A。如果不启动应急调度方案，污染物达标时间则长达74.6 h，如果不考虑电能损失，污染物最短可在14.6 h后达标，所需时间减少80.4%。这充分说明应急调度稀释了污染物的浓度，验证了模型及算法的有效性。为进一步说明模型的有效性，我们选取方案A、C和F来观察突发水污染事件发生6 h后，不同调度方案中高坝洲水库以下的沿程污染物浓度变化过程(图3)。模拟结果表明，随着下泄流量的增大，经历相同的时长后，污染物浓度峰值降低，运移的位置更远，说明水库释放的水流对污染物起到稀释和加速迁移的作用。事实上，图4的动态模拟结果也显示了应急调度中污染物会随着时间而迁移与稀释。这些图表均验证了模型与算法的有效性。

Figure 2. Pareto front after optimization

图2. 优化后的得到的Pareto前沿

Table 1. Scheduling result of emergency

表1. 应急调度结果

注1：优化结果若表示该水库没有启动调度时， $\left(t_1,Q_m,t_{last}\right)$ 统一用表示。

注2：时间的单位为小时，电能的单位为万千瓦时，流量单位为立方米每秒。

Figure 3. Distribution of pollutant concentrations six hour after pollution incident

图3. 污染事件发生6 h后污染物浓度

Figure 4. Concentration of phenol at confluence between QingJiang River and Yangtze River

图4. 清江–长江交汇处污染物浓度变化过程

通过表1的数据分析，发现水布垭、隔河岩两座水库在不同调度方案中均没有加大放水。由经验及逻辑推断，这两座水库未参与应急调度的原因是他们没有与被污染河段直接相连且相距较远。若加大放水，会破坏水库原有的运行方式，降低水能利用效率，但是却不能直接影响污染物的迁移扩散过程，因此在多目标进化计算中，加大水布垭、隔河岩水库放水这种调度方案会作为一个劣解被淘汰。因此，当发生突发性污染事件需要启动应急调度时，在下游水库的水位、库容允许的情况下，优先调用距离污染物较近的或与被污染河段直接相连的水库，而后再考虑水量补偿。

3.3. 应急调度的高效益区间

从不启动应急调度的F方案开始，通过增大水库的放水，达标时间不断减少，同时损失的电能也在增加，但变化速率却不是恒定的。根据列表2的数据，E方案的达标时间比F方案减少15.7小时，电能的损失增加了2.5万千瓦时，说明达标时间每减少一个小时平均多损失1600千瓦时的电能，而A方案的达标时间虽然比B方案只减少了1.6个小时，但电能的损失却多增加了7.7万千瓦时，说明每减少一个小时的达标时间就多损失4.81万千瓦时的电能，两者相差三十倍。

Table 2. Benefits and sacrifice of emergency dispatching

表2. 应急调度的收益与损失

Figure 5. Subset with high benefit of emergency dispatching scheme set

图5. 应急调度方案集的高效益区间示意图

列表2的数据说明，从方案F递变至方案A，每减少单位达标时间所多增加的电能损失在不断增大。原因是多方面的：一方面，随着水库不断增大放水，由于河流的蓄水增多，释放水量对稀释作用的提升效果在减缓，再者，由于河流横截面积变大，流速增加的速率变慢，因而释放水量对加速迁移作用的提升效果也在减缓；另一方面，随着下泄水量的增多，水库水位不断下降从而导致出力不断降低，水能利用效率不断下降，应急调度的代价加速增长。因此，综合衡量收益与损失，给出应急调度的高效益区间(见图5)。

点P是距离直线AF最远的点，称之为“最经济点”。连接不调度方案F与最大限度调度方案A的斜率代表：按照线性速度，达标时间每减少一个小时所造成的电能损失平均量。P点与A点之间的方案，减少达标时间而造成电能损失的速度比线性速度快，因此成本高；而P点与F点之间的方案，减少达标时间而造成电能损失的速度比线性速度慢，因而是“高效益区间”。因此，若在险情允许的情况下，建议根据实际情况(如控制污染物达标时间的预期)，在点P与点F之间选取合适的应急调度方案，一般不建议选P点与A点之间的方案。

4. 结论

本文根据水动力模型和一维污染物对流–扩散模型，以污染物达标时间最短和应急调度过程中损失的电能最小为目标，充分发挥梯级水库群的调度作用，将模拟与优化结合起来，建立了基于模拟–优化模式的梯级水库群突发水污染事件应急调度优化模型，并借助改进的NSGA-II算法求解模型。所建模型成功应用于清江流域水布垭–隔河岩–高坝洲梯级水库群突发水污染事件应急调度，得到了一组最优应急调度方案集。优化计算得到的最优应急调度方案在减少电能损失的情况下使得污染物浓度下降明显，突发水污染事件得到控制。该模型对梯级水库群突发水污染事件应急调度具有一定的应用价值。

文中主要考虑了应急调度下造成的电能损失，暂时没有考虑损失水量对后续常态调度的影响，例如因水头降低而导致在常态调度期间带来的发电损失等，这是下一个值得研究的课题。应急调度涉及到来水情况、地形资料与各个水电站资料，不确定因素及各种误差在所难免，因此在模型应用时要根据具体情况注意误差的控制。

基金项目

十三五国家重点研发项目(2016YFC0402207)。

参考文献