1. 引言
设
和
是正整数,则一个参数为
的二维光正交码,C (简单记作
),是满足特定条件的
阶
-矩阵(码字)的集合,其中k,
和
分别称为该正交码的权重,自相关值和互相关值。令
表示
中所有k元组的集合,其中
, 是模m的剩余类加法群。设C是一给定的二维光正交码,对每个
是模m的剩余类加法群。设C是一给定的二维光正交码,对每个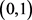 -矩阵
-矩阵 ,令其行标和列标分别取值于集合
,令其行标和列标分别取值于集合 和
和 ,使得
,使得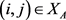 当且仅当矩阵A的元素
当且仅当矩阵A的元素 。于是,二维
。于是,二维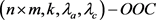 ,C,可以视作集合
,C,可以视作集合 的一个子集,其元素满足下列两个条件:
的一个子集,其元素满足下列两个条件:
1) 自相关性:对任意 和每个
和每个 ,有
,有 ;
;
2) 互相关性:对任意的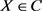 ,
, 且
且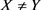 和每个
和每个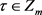 ,有
,有 。
。
其中 且所有加法模m计算。
且所有加法模m计算。
当 时,一个
时,一个 通常称作一维
通常称作一维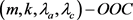 。二维光正交码中所含码字个数称为其容量。对给定的正整数n和m,用
。二维光正交码中所含码字个数称为其容量。对给定的正整数n和m,用 表示所有
表示所有 的最大容量。若
的最大容量。若 ,上述符号可简写为
,上述符号可简写为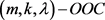 和
和 。
。
光正交码是为码分多址(OCDMA)光纤信道而设计的一种专用码。光正交码的研究始于1989年 [1] 。关于一维光正交码已有许多研究结果,参见文献 [2] [3] 及其中所列参考文献。实际应用,需要大容量相关性能好的光正交码。二维光正交码正是为克服一维光正交码的码字长,稳定性差等不足而提出的。二维光正交码的研究主要集中在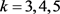 的情况,参见文献 [4] 中所列的参考文献。当
的情况,参见文献 [4] 中所列的参考文献。当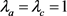 时,王建民等 [5] ,冯弢等 [2] 和王小苗等 [6] 给出
时,王建民等 [5] ,冯弢等 [2] 和王小苗等 [6] 给出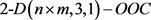 ,
, 的最大容量及部分无限类的构造方法。本文确定当
的最大容量及部分无限类的构造方法。本文确定当 时,
时,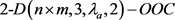 的最大容量,并给出直接构造法。我们主要证明
的最大容量,并给出直接构造法。我们主要证明
定理1. 设n和m是正整数,则

2. 基础知识
下面先介绍在证明结论时所涉及到的基本概念和相关结论。
对任意的 和
和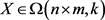 ,定义
,定义 ,称为X的平移。于是,群
,称为X的平移。于是,群 作用于
作用于 。集合
。集合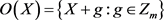 称为X所生成的轨道。包含m个元素的轨道称为长轨道,否则称为短轨道。显然,在群
称为X所生成的轨道。包含m个元素的轨道称为长轨道,否则称为短轨道。显然,在群 的作用下集合
的作用下集合 被划分成若干个轨道。
被划分成若干个轨道。
设 。对任意
。对任意 ,定义X的
,定义X的 -纯差是一个多重集合
-纯差是一个多重集合 ,其中加法模m计算。再令
,其中加法模m计算。再令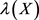 表示多重集
表示多重集 中元素的最大重数。于是由文献 [4] ,
中元素的最大重数。于是由文献 [4] ,
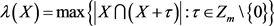 (1.1)
(1.1)
例1. 下列四个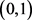 -矩阵构成一个
-矩阵构成一个 。
。
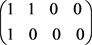 ,
,  ,
,  ,
, 
通过标记矩阵中1的位置,四个矩阵可以转换成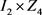 上的四个3-元组
上的四个3-元组
 ,
,  ,
,
 ,
, 
3. 当 时,
时, 的最大容量
的最大容量
根据二维光正交码的定义和式(1.1),不难证明一个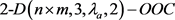 ,C,是集合
,C,是集合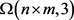 在群
在群 作用下一些长轨道代表元X的集合。从而
作用下一些长轨道代表元X的集合。从而 是
是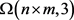 在群
在群 作用下满足
作用下满足 的长轨道
的长轨道 的个数。
的个数。
我们在文献 [4] 中证明了一个 的最大容量就是集合
的最大容量就是集合 在群
在群 作用下所有长轨道个数。
作用下所有长轨道个数。
引理2.1:( [4] )设n,m和k是正整数。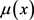 是莫比乌斯函数,则
是莫比乌斯函数,则

因此 恰好是
恰好是 在群
在群 作用下所有长轨道的个数。因此引理2.1中取
作用下所有长轨道的个数。因此引理2.1中取 得下面的推论。
得下面的推论。
推论2.2:设n和m是正整数。则

由平移的定义,一个 的轨道代表元的形式总可以写作
的轨道代表元的形式总可以写作 , 其中
, 其中 ,并且可以分如下三种形式:
,并且可以分如下三种形式:
形式1: 且
且 ;
;
形式2: ;
;
形式3: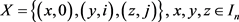 ,
, 互不相同且
互不相同且 。
。
令 表示码字
表示码字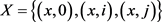 的导出组。定义
的导出组。定义 的差集为多重集合
的差集为多重集合 ,并且
,并且 中基础元素的集合又称为
中基础元素的集合又称为 的支集,记作
的支集,记作 。则由文献 [3] 的引理2.2得
。则由文献 [3] 的引理2.2得
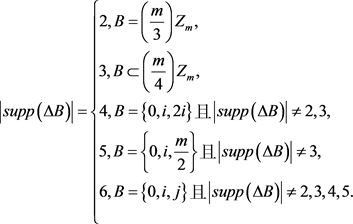
由此可得下列结论:
引理2.3:设m是正整数。码字 满足
满足 当且仅当
当且仅当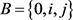 有下列形式之一:
有下列形式之一:
1) ;
;
2) ,其中
,其中 ,
, ;
;
3)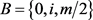 ,其中
,其中 。
。
设Q是 在群
在群 作用下的任意轨道。若
作用下的任意轨道。若 ,则
,则 且
且 。于是,有下列结论:
。于是,有下列结论:
引理2.4:对 ,若
,若 ,则X只能有下列形式之一:
,则X只能有下列形式之一:
1)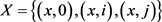 ,其中
,其中 ,
, 且
且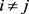 ;
;
2)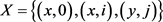 ,其中
,其中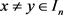 ,
, 且
且 。
。
4. 当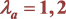 时,
时, 的最大容量
的最大容量
为确定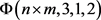 的值,我们首先要确定满足条件
的值,我们首先要确定满足条件 的所有长轨道的个数。令
的所有长轨道的个数。令 表示
表示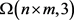 在群
在群 作用下所有满足条件
作用下所有满足条件 的长轨道
的长轨道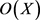 的集合。根据引理2.4,
的集合。根据引理2.4, 可以写成两个互不相交的集合的并,不妨设
可以写成两个互不相交的集合的并,不妨设 , 其中
, 其中
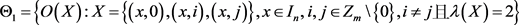 ;
;

于是, 。下面分别计算
。下面分别计算 和
和 的大小。
的大小。
根据引理2.3, 又可以写成下列三个互不相交的子集合的并,
又可以写成下列三个互不相交的子集合的并, ,其中
,其中
 ;
;
 ;
;
 。
。
引理3.1:设n和m是正整数,若 ,则
,则 ,否则为0。
,否则为0。
证明:根据集合 的定义,对给定的
的定义,对给定的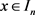 ,若
,若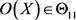 ,则
,则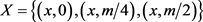 ,
, 或
或 。显然此三个区组属于同一条轨道。于是,结论得证。
。显然此三个区组属于同一条轨道。于是,结论得证。
引理3.2:设n和m是正整数,则
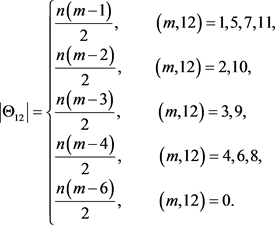
证:设Q是 中任意轨道,则必有
中任意轨道,则必有 ,
, 且
且 使得
使得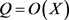 。故
。故 。再令
。再令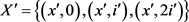 ,
,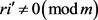 且
且 。若X和
。若X和 属于同一条轨道,则总存在某个
属于同一条轨道,则总存在某个 使得
使得 。这等价于
。这等价于 ,即,
,即, 且
且 。由此得
。由此得 。若
。若 ,则
,则 。由此得
。由此得 ,否则若
,否则若 ,
,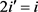 。于是得
。于是得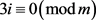 ,这与
,这与 的定义矛盾。若
的定义矛盾。若 ,则
,则 。由此得
。由此得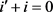 ,
, 或
或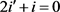 ,
,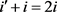 。经计算仍得
。经计算仍得 ,矛盾。若
,矛盾。若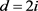 ,则
,则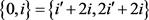 。由此得
。由此得 ,即
,即 。否则若
。否则若 ,则仍得
,则仍得 ,矛盾。综上分析,若X和
,矛盾。综上分析,若X和 属于同一条轨道,则
属于同一条轨道,则 。反之显然。故,
。反之显然。故, ,其中
,其中 表示满足方程
表示满足方程 ,
, 的
的 的个数。经详细计算引理结论得证。
的个数。经详细计算引理结论得证。
引理3.3:设n和m是正整数。则

证:证明过程与引理3.1类似。
引理3.4:设n和m是正整数。则
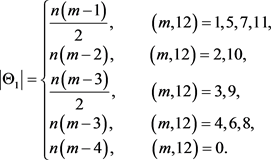
证:由 ,且
,且 互不相交,故
互不相交,故 。经详细计算结论得证。
。经详细计算结论得证。
引理3.5:设n和m是正整数。则

证:设Q是 中任意一条轨道。则由引理2.3知,必存在
中任意一条轨道。则由引理2.3知,必存在 使得
使得 ,其中
,其中 且
且 。而且
。而且 ,
, 。这里
。这里 ,否则
,否则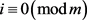 ,这与
,这与 矛盾。因此若
矛盾。因此若 ,则
,则 当且仅当
当且仅当 即
即 。于是,若
。于是,若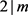 ,则集合
,则集合 可以改写为
可以改写为

为确定 中轨道个数,我们定义映射
中轨道个数,我们定义映射 使得
使得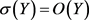 。对任意
。对任意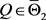 ,下面先确定
,下面先确定 的值。
的值。
设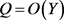 ,其中
,其中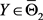 。若
。若 ,其中
,其中 ,
,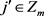 。则
。则 ,故存在
,故存在 使得
使得 ,即
,即 ,这等价于
,这等价于 且
且 。由此得
。由此得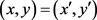 且
且 或
或 。于是
。于是 。反之显然。故
。反之显然。故

这表明,对任意的 ,有
,有 。故,
。故, 。
。
根据前面引理的结果定理1证明如下:
证:根据引理2.1,得 ,其中
,其中 再结合推论2.2,引理3.4,和引理3.5,加以详细计算定理的结论得证。
再结合推论2.2,引理3.4,和引理3.5,加以详细计算定理的结论得证。
5. 码字结构
根据前面分析,我们给出最大二维 的直接构造法。
的直接构造法。
一个最大二维 的任意码字X满足
的任意码字X满足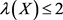 ,所以
,所以 的码字中舍掉
的码字中舍掉 的码字,剩余的码字既是最大二维
的码字,剩余的码字既是最大二维 的所有码字。既有
的所有码字。既有
定理2:设n是任意正整数,一个最大二维 的码字结构如下:
的码字结构如下:
 时,
时,
1)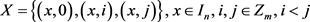 且
且 ;
;
2) ;
;
3) ,互不相同且
,互不相同且 。
。
 时,
时,
1) 且
且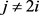 ;
;
2)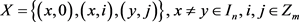 且
且 ;
;
3) ,互不相同且
,互不相同且 。
。
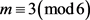 时,
时,
1) 且
且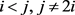 ;
;
2)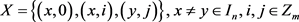 ;
;
3)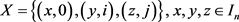 ,互不相同且
,互不相同且 。
。
定理3 设n是任意正整数,一个最大二维 的码字结构如下:
的码字结构如下:
 时,
时,
1) 且
且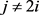 ;
;
2) 且
且 ;
;
3) 互不相同且
互不相同且 。
。
 时,
时,
1) 且
且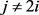 ;
;
2) ;
;
3) 互不相同且
互不相同且 。
。
 时,
时,
1) 且
且 ;
;
2) 且
且 ;
;
3) 互不相同且
互不相同且 。
。
 时,
时,
1)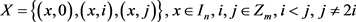 且
且 ;
;
2) ;
;
3)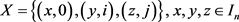 互不相同且
互不相同且 。
。
 时,
时,
1) 且
且 ;
;
2)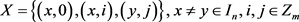 且
且 ;
;
3) 互不相同且
互不相同且 。
。
 时,
时,
1) 且
且 ;
;
2) 且
且 ;
;
3)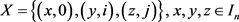 互不相同且
互不相同且 。
。
本文用组合计数和代数方法,对任意正整数n,m和 ,确定了二维光正交码
,确定了二维光正交码 的最大容量,并给出相应码字结构。希望我们的结果对权重为3的二维光正交码最大容量和码字构造问题的研究的完善有一定的参考价值。
的最大容量,并给出相应码字结构。希望我们的结果对权重为3的二维光正交码最大容量和码字构造问题的研究的完善有一定的参考价值。
基金项目
本文得到国家自然科学基金项目(11401326、11271042和11601137);内蒙古自然科学基金项目(2015MS0125、2015BS0103和NJZC16049);内蒙古自治区高等学校“青年科技英才支持计划”(NJYT-17-B12),内蒙古师范大学科研启动基金(2013YJRC026)的支持。
NOTES
*通讯作者。