1. 引言
目标跟踪技术最早应用于军事领域,即世界上第一部跟踪雷达站。直到20世纪70年代卡尔曼滤波理论 [1] 的提出才让目标跟踪真正得到广泛关注。随着计算机技术的发展与科技的进步,视频目标跟踪技术在更广阔的领域得到了应用。视频目标跟踪方法融合了图像处理、模式识别、人工智能等多个领域的研究成果,在军事、工业、科学等 [2] [3] [4] [5] [6] 方面具有实用价值及良好的发展前景。
粒子滤波理论 [7] [8] 为非线性、非高斯条件下的跟踪问题提供了解决方法。粒子滤波 [9] 是一种基于蒙特卡罗仿真实现非线性递推贝叶斯滤波的算法,它使用一组带有权值的随机样本集对后验概率密度进行近似。由于粒子滤波不受线性、高斯分布以及维数的限制,适用于任何状态空间模型,且精度可逼近最优估计,因此粒子滤波拥有广阔的应用前景,也是目标跟踪领域的研究热点之一。
在视频目标跟踪过程中,目标的姿态变化、光照变化、环境的复杂度等都会对跟踪造成极大的困难。文献 [10] [11] 利用目标的边缘、颜色信息来刻画目标特征,提高特征表达的鲁棒性;文献 [12] 建立自适应模型缓解光照变化对跟踪结果的影响;文献 [13] 提出一种基于颜色特征的自适应粒子滤波算法,利用颜色分布和模板匹配进行目标跟踪。
本文主要研究了文献 [13] 的粒子滤波算法,包括构建动态系统、学习目标的颜色分布、模板更新机制,实现了基于粒子滤波的视觉目标跟踪算法。最后通过模拟实验和真实场景对算法的跟踪性能进行了验证。
2. 基本粒子滤波
粒子滤波是在理论上可实现最小方差的非线性滤波器,它可以有效处理高维、非线性、非高斯问题,具有很强的灵活性。粒子滤波的思想是用一组带有相关权值的离散随机样本(即粒子)来近似表征目标的后验概率密度函数。首先通过状态转移函数预测粒子可能的状态,再从序列重要性采样中递推得到粒子权值,利用蒙特卡罗仿真由粒子加权估计值来逼近真实的后验概率密度,从而实现递推贝叶斯滤波。
假设从分布已知的重要性函数 [14] 中采样得到粒子
,并给每个粒子赋予权值:
(1)
其中,
表示第i个粒子在0到
时刻的状态,
表示k时刻的观测值,
为似然函数,
为粒子的状态转移概率。
由蒙特卡罗仿真可知,目标的后验概率密度可表示为:
(2)
其中N表示粒子个数,
为归一化的重要性权值。
随着时间推移,粒子在传播过程中极易产生粒子退化现象。对于粒子的退化程度,我们可以用有效采样尺度
[15] 来度量:
(3)
其中
为归一化权值。由上式可以看出
,
越小退化问题越严重。当权重方差接近于零时便得到最优估计。本文采用文献 [13] 中的重采样方法,在序列重要性采样的基础上再对粒子集进行N次采样,保留大权值粒子,消除小权值粒子,从而产生新的粒子集
,提高样本的有效性,解决粒子退化问题。
3. 粒子滤波视觉目标跟踪算法
本文主要研究了基于颜色特征的粒子滤波跟踪算法,利用颜色特征表达目标,通过目标模板与候选模板的相似度匹配来计算粒子权值,并实时更新目标模板,实现更加稳定的跟踪。
3.1. 视觉特征提取
本文利用文献 [13] 中引入核函数的颜色直方图来描述目标的视觉信息。颜色是人类视觉中获取目标信息的主要特征,颜色特征对于目标的旋转、尺度变化都具有较强鲁棒性。本文采用典型的
RGB颜色空间描述颜色分布。
在计算目标区域的颜色直方图时,为了更加准确的描述目标的颜色特征,引入一个核函数,
(4)
其中r表示距中心点的距离。因为在选取目标时边界像素点很可能属于背景,为了增加颜色模型的可靠性,对离目标中心点远的粒子赋予较小的权值,而距中心点近的粒子赋予较大权值。
假设所选择目标区域的中心点为
,目标区域内像素的位置为
,那么此区域的颜色分布
可表示为:
(5)
式中I表示区域内的像素个数,δ为单位冲击函数,a为自适应变量:
(6)
其中
、
为所选区域的半宽和半高,a会随着区域大小的变化而自适应变化。公式(5)中f为归一化常数,
(7)
3.2. 状态空间模型
目标跟踪的本质是估计目标的运动状态。为了得到目标状态的估计值,要先建立相应的状态空间模型,对状态空间模型中的参数进行估计,从而得到目标状态,实现目标跟踪。
状态空间模型是一种表示时间序列的方法,它通过系统的状态向量来描述时间序列的演变,状态向量中包含了所要研究系统的全部相关信息,并通过观测向量来描述与状态相关的噪声观测量。
3.2.1. 系统状态转移模型
假设从粒子滤波中采样得到的粒子集
,每个粒子
可表示如下:
(8)
其中
表示粒子位置,
表示跟踪框的半宽和半高。
在动态系统中系统状态转移就是粒子随时间更新的过程,称为粒子传播,服从一阶ARP (Auto-Regressive Process)自回归过程方程:
(9)
其中
表示k时刻粒子状态,
、
为常数,
是高斯随机噪声。从上式可以看出,预测k时刻的粒子状态
只与
时刻的粒子状态
和噪声
有关,不需要得到观测值
。
3.2.2. 观测模型
将状态转移得到的粒子集
作为候选模板
,对其进行观测。跟踪过程中每一时刻都会获得新的观测信息
,通过观测值来估计粒子状态。为了衡量候选模板
与目标模板
的相似度,定义巴氏距离(Bhattacharyya distance):
(10)
其中ρ表示巴氏系数(Bhattacharyya Coefficient),定义如下:
(11)
公式(10)表明,巴氏距离d越小两种分布的颜色相似度越高,反之相似度越低。对相似性高的粒子赋予较大的权值,相似性低的粒子赋予较小权值,由此计算每个粒子的权值:
(12)
其中i表示第i个粒子(
),σ表示协方差,d表示巴氏距离,ρ表示巴氏系数,
为第i个粒子的候选模板,q为目标模板。
由蒙特卡洛仿真可知,最终目标的估计状态为:
(13)
3.3. 模板更新
在跟踪过程中光照、视角、背景等会不断发生变化,为了克服目标和环境变化对跟踪结果的影响,及时地对目标模板进行更新。定义模板更新公式:
(14)
其中
表示k时刻的目标模板,
表示粒子估计状态的颜色直方图,α为更新参数。通过模板更新,在目标模板中不断加入得到的观测信息可以更真实的反应目标状态,从而提高跟踪的精确度。
3.4. 粒子滤波目标跟踪流程
本文主要介绍了基于颜色特征的粒子滤波视觉目标跟踪算法。首先,初始化粒子集
,权值为
,并建立目标模板q。通过系统状态转移模型预测k时刻的粒子集
,建立候选模板p。在系统观测阶段,度量候选模板p和目标模板q的颜色分布的相似度,得到粒子权值
,估计目标状态
。再利用重采样算法,得到新的粒子集进入下一帧迭代过程。
基于颜色特征的粒子滤波视觉目标跟踪算法流程如表1所示。
4. 实验结果
4.1. 仿真实验
假设时间离散的非线性动态系统方程为:

Table 1. Particle filter tracking algorithm flow based on color features
表1. 基于颜色特征的粒子滤波跟踪算法流程
(15)
(16)
实验中令
,
,粒子状态初始值
,迭代次数
,粒子采样数
。图1为粒子滤波在非线性系统下状态估计值与真实值的比较。图中星号表示真实值,曲线表示粒子滤波的估计值。从图1可以看出,粒子滤波基本实现了对真实值的估计,但仍存在一定的偏差,其均方误差
。
4.2. 真实跟踪场景
本文分别在简单场景和复杂场景下对粒子滤波的跟踪性能进行实验。
实验视频1:如图2所示,男子匀速从镜头右侧走向左侧,背景没有明显的动态变化,对男子进行跟踪实验。视频序列长度为77帧,帧速率为15帧/秒,图像大小为
。
实验视频2:如图3所示,飞行器在空中进行左右上下平移,摄像头跟随飞行器拍摄,背景不断变化,环境复杂且存在很多干扰,对飞行器进行跟踪。视频序列长度为213帧,帧速率为15帧/秒,图像大小为
。
从图2中可以看出,在无干扰、无遮挡的简单静态场景下,粒子滤波可以稳定的跟踪目标。在图3的视频序列中有行人干扰、背景杂乱,且产生光照变化,目标处于复杂的跟踪环境中。本文算法仍能准确跟踪飞行器,中心点也未发生偏移。可见粒子滤波在复杂的非线性非高斯情况下,可以实现稳定跟踪,并且对于动态干扰和光照变化具有较强的鲁棒性。
5. 小结
本文主要研究了基于颜色特征的粒子滤波跟踪算法,利用颜色直方图描述目标特征,通过模板匹配
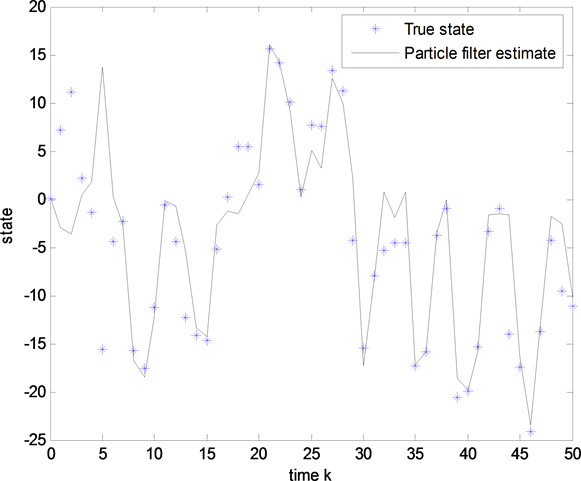
Figure 1. State estimation in Particle filter
图1. 粒子滤波状态估计

Figure 2. Particle filter tracking results in a simple scenario
图2. 简单场景下的粒子滤波跟踪结果

Figure 3. Particle filter tracking results in complex scenes
图3. 复杂场景下的粒子滤波跟踪结果
计算粒子权值,并实时更新目标模板,以实现更加稳定的跟踪。实验结果表明,本文算法在简单或复杂场景下都能准确地跟踪目标,具有较强的鲁棒性。
计算粒子权值,并实时更新目标模板,以实现更加稳定的跟踪。实验结果表明,本文算法在简单或复杂场景下都能准确地跟踪目标,具有较强的鲁棒性。
参考文献