电磁场下Pre-BO^¨ tzinger Complex神经元的放电活动研究

Discharge Pattern of Neuron in the Pre-BO^¨ tzinger Complex under Magnetic Field

摘要: 磁场对神经元的放电模式有重要影响。忆阻器的功能类似于神经元突触的可塑性，可用其模拟磁通量。在Butera动力学模型的基础上引入忆阻器，研究Pre-Bӧtzinger复合体在磁流作用下复杂的放电模式。在钾电导变化条件下，利用快慢分析和双参数分岔分析的方法，研究呼吸系统神经元放电活动模式产生和转迁的动力学机制。

Abstract: Magnetic field has important effects on the firing activities of neuron. The function of memristor is similar as that of plasticity of synapse. Based on the Butera dynamic model added with memristor, the discharge pattern of pre-Bӧtzinger complex under the magnetic flux is studied. By fast-slow analysis and two-parameter bifurcation analysis, the dynamic mechanisms of the discharge pattern of neurons in the pre-Bӧtzinger complex are studied with the potassium conductance varying.

1. 引言

呼吸是一种复杂的节律性运动，Smith [1] 等提出位于哺乳动物延髓外侧区的Pre-Bӧtzinger复合体与呼吸节律的产生有密切联系。这是因为Pre-Bӧtzinger复合体中存在一些吸气神经元，其可以自主的发出一定频率的冲动，即神经元的放电活动。神经元系统是相当复杂的，所以神经元模型必须足够复杂才可以用来描述神经元细胞的动力学行为。对神经科学的研究也在不断的深入，神经元放电模式可受到神经元膜电容、平衡电位以及离子通道电导等电生理参数影响 [2] ；神经元的同步活动可以由兴奋性突触耦合促进 [3] ；噪声对神经元系统的编码也有影响，可以改变膜电位的振荡时间、振幅大小以及节律模式 [4] 。

近年来，探究电磁辐射对大脑的作用已成为热点。一方面，神经元系统中可以检测到电磁场的复杂分布，并且当信息在神经元之间传递时，会产生磁流的波动以及跨膜磁通量的变化。研究表明，磁流对耦合神经元同步放电模式有很大影响 [5] [6] ；电磁辐射也影响神经元放电节律的转迁 [7] ；李洪明等人研究了恒电流刺激下的神经元Chay模型，通过控制恒电流可以使系统发生Hopf分岔 [8] 。另一方面，人们生存的环境中电磁辐射不断的增加，可能会引起相关的神经性疾病，如研究表明长时间的电磁辐射可能引起帕金森氏症和阿尔兹海默症 [9] [10] 。

忆阻器具有记忆的特点，其功能类似于神经元突触的可塑性，可用其表示膜电位和磁通量的关系。本文以添加忆阻器的Butera动力学模型为研究对象，来描述膜电位与磁流之间的相互作用。主要研究刺激电流恒定时，钾电导浓度的改变对系统放电规律的影响。研究结果为深入了解电磁辐射对人体神经元的影响提供有益的探讨。

2. 模型

具有忆阻器的Pre-Bӧtzinger复合体中神经元模型 [11] 如下：

$\{\begin{array}{l}\frac{\text{d}v}{\text{d}t}=\left(-I_{Nap}-I_{Na}-I_K-I_L-I_{tonic}-I_{app}\right)/C(1)\\ \frac{\text{d}h}{\text{d}t}=\epsilon \left(h_{\infty }\left(v\right)-h\right)/{\tau }_h\left(v\right)(2)\\ \frac{\text{d}n}{\text{d}t}=\left(n_{\infty }\left(v\right)-n\right)/{\tau }_n\left(v\right)(3)\\ \frac{\text{d}\phi }{\text{d}t}=f\left(\phi \right)(4)\\ \frac{\text{d}q\left(\phi \right)}{\text{d}\phi }=\rho \left(\phi \right)(5)\end{array}$

其中， $I_{Nap}$ 、 $I_{Na}$ ， $I_K$ 和 $I_L$ 分别代表持续钠电流、钠电流、钾电流和漏电流。 $I_{tonic}$ 是细胞膜受到兴奋性刺激所产生的电流，各离子电流动力学的模型描述为：

$I_{Nap}=g_{Nap}{m}_{p,\infty }\left(v\right)h\left(v-E_{Na}\right)$ ， $I_{Na}=g_{Na}{m}_{\infty }^3\left(v\right)\left(1-n\right)\left(v-E_{Na}\right)$ ，

$I_K=g_K{n}^4\left(v\right)\left(v-E_k\right)$ ， $I_L=g_L\left(v-E_L\right)$ ， $I_{tonic}=g_{tonic\text{-}e}\left(v-E_{syn\text{-}e}\right)$ ，

$I_{app}=k_1\ast v\ast \rho \left(\phi \right)$ ， $f\left(\phi \right)=v-k_2\ast \phi$ 。

$\rho \left(\phi \right)$ 是指磁通控制忆阻器，用来描述磁通量φ与v之间的关系，其表达式为： $\rho \left(\phi \right)=\alpha +3\beta {\phi }^2$ ，其中 $\alpha ,\beta$ 是给定的参数值。参数 $k_1$ 对膜电位上的电流起到调节作用， $k_2$ 用来抑制磁通量的增加。其它函数的具体表达式以及参数的取值详见附录。

3. 神经元放电行为转迁的分析

我们用快慢动力学分析的方法，研究神经元的放电类型和特征。因为参数ε是一个很小的量，可以把整个系统分为快慢两个系统。其中，方程(1)、(2)、(4)为快子系统，(3)为慢子系统。当外部刺激参数 $k_1=0.05$ ， $k_2=2$ ， $\alpha =2$ ， $\beta =0.0005$ 取定时，改变钾离子电导的浓度会呈现不同的放电模式。

当 $g_K=5$ 时，在不考虑和考虑磁通量并添加磁流忆阻器的条件下，神经元的放电模式分别如图1(a)，

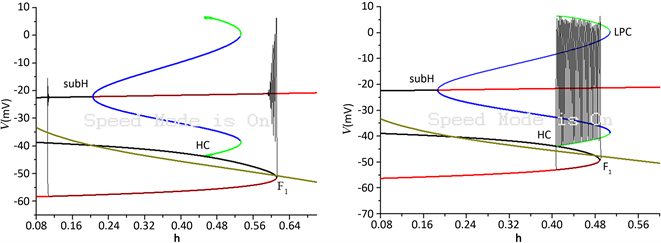(a) (b)(c) (d)

Figure 1. Neuronal discharge patterns and fast/slow bifurcation analysis with $g_K=5$ . (a) Membrane potential under conditions no magnetic flow with $I_{app}=0,f\left(\phi \right)=0,\rho \left(\phi \right)=0$ ; (b) The time series of membrane potential under magnetic flow with $k_1=0.05,k_2=2,\alpha =2,\beta =0.0005$ ; (c) Fast/slow bifurcation analysis of bursting under the same parameter set as that of (a); (d) fast/slow bifurcation analysis of bursting under the same parameter set as that of (b)

图1. $g_K=5$ 时神经元的放电模式及快慢分岔分析。(a) $I_{app}=0,f\left(\phi \right)=0,\rho \left(\phi \right)=0$ ，即不受磁流影响条件下膜电位的时间序列；(b) 磁流满足条件 $k_1=0.05,k_2=2,\alpha =2,\beta =0.0005$ 时的膜电位的时间序列；(c) 对应于图(a)的快慢分析；(d) 对应(b)的快慢分析

图1(b)所示。慢子系统的变量h作为参数，快子系统参数在平面 $\left(h,v\right)$ 上的分岔分别如图1(c)，图1(d)所示。快子系统对于慢变量h的分岔曲线是一条S型曲线，其中，红色和黑色曲线分别表示稳定和不稳定平衡点，绿色和蓝色分别表示稳定和不稳定极限环。平衡点的上支由稳定和不稳定焦点组成，不稳定焦点经由亚临界Hopf分岔(subH)变为稳定焦点。由亚临界Hopf分岔产生的不稳定极限环与稳定极限环在极限环的鞍结分岔(LPC)处相遇，稳定极限环通过同宿轨分岔(HC)消失。

当神经元不受磁流的影响时，放电模式及相应的快慢分岔分析分别如图1(a)和图1(c)所示。平衡点的下支由稳定结点组成，稳定结点与中支的不稳定鞍点相遇并发生平衡点的鞍结分岔(F₁)。当慢变量h增大时，轨线下支的静息态经由鞍结分岔点(F₁)快速跃迁至S型曲线上支的稳定焦点，并围绕稳定焦点振荡，且振幅逐步减弱，最终收敛到稳定的焦点。轨线经过亚临界Hopf分岔点到上支的不稳定焦点，由于不稳定焦点的性质，轨线逐步远离不稳定焦点而振荡，最后回到曲线下支的稳定结点。从而，放电模式为“subHopf/subHopf”型簇放电，如图1(c)所示。

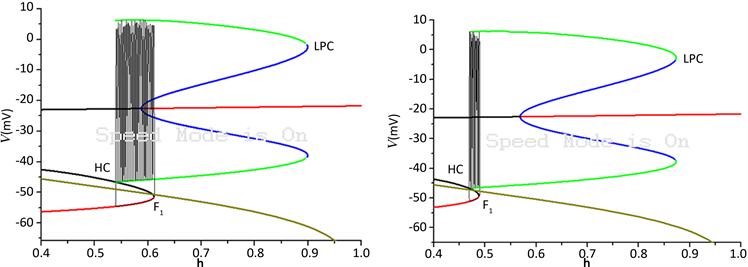(a) (b)(c) (d)

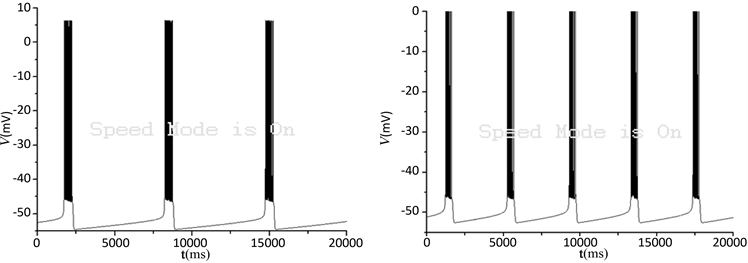
Figure 2. Neuronal discharge patterns and fast/slow bifurcation analysis with $g_K=8.5$ . (a) Membrane potentialunder conditions no magnetic flow with $I_{app}=0,f\left(\phi \right)=0,\rho \left(\phi \right)=0$ ; (b) The time series of membrane potential under magnetic flow with $k_1=0.05,k_2=2,\alpha =2,\beta =0.0005$ ; (c) Fast/slow bifurcation analysis of bursting under the same parameter set as that of (a); (d) fast/slow bifurcation analysis of bursting under the same parameter set as that of (b)

图2. $g_K=8.5$ 神经元的放电模式及快慢分岔分析。(a) $I_{app}=0,f\left(\phi \right)=0,\rho \left(\phi \right)=0$ ，即不受磁流影响条件下膜电位的时间序列；(b) 磁流满足条件 $k_1=0.05,k_2=2,\alpha =2,\beta =0.0005$ 时膜电位的时间序列；(c) 对应于图(a)的快慢分析；(d) 对应(b)的快慢分析

当神经元受磁流的影响时，放电模式及相应的快慢分岔分析分别如图1(b)和图1(d)所示。快子系统对慢变量h的分岔结构与不受磁流的影响情况下类似，但神经元的放电模式发生了改变。轨线的静息态经由平衡点的鞍结分岔F₁跃迁至上支的稳定极限环，并由于极限环的吸引反复振荡。振荡态经由极限环同宿轨分岔(HC)跃迁至下支的静息态，从而放电模式为“fold/homoclinic”型簇放电。

上述结果表明，当 $g_K=5$ 时，神经元受到电磁场的影响时，其放电模式从“subHopf/subhopf ”型簇电转变为“fold/homoclinic”型簇放电，且神经元的放电周期明显减小。

当钾电导增加至 $g_K=8.5$ 时，神经元的放电模式和对应的快慢分析如图2所示。受到磁流的影响，簇中所包含的峰的个数减少，同时簇放电的放电周期变小，频率增大，分别如图2(a)和图2(b)所示。对应的快慢分析分别如图2(c)和图2(d)所示，图中曲线和分岔点的表示含义同图1。

系统轨线都是经由平衡点的鞍结分岔(F₁)跃迁至上支的稳定极限环，之后受极限环的吸引反复振荡(放电态)，最后放电态由于极限环的同宿轨分岔 跃迁至下支的静息态，放电模式即为

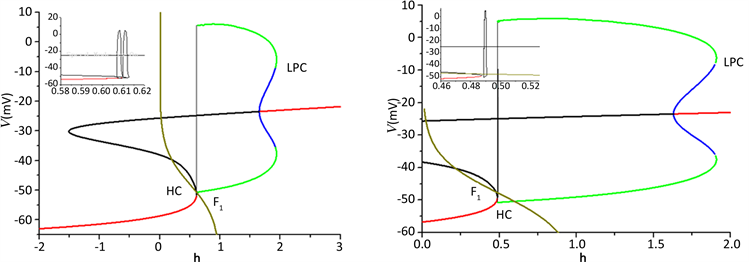(a) (b)(c) (d)

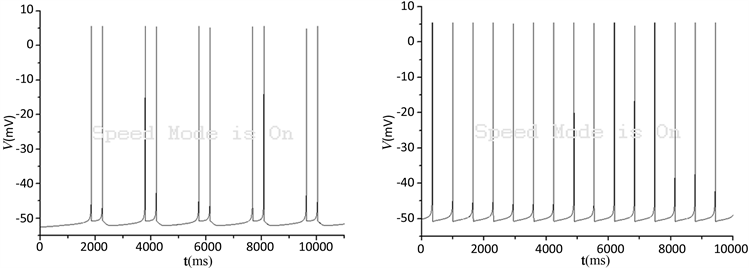
Figure 3. Neuronal discharge patterns and fast/slow bifurcation analysis with $g_K=20$ . (a) Membrane potentialunder conditions no magnetic flow with $I_{app}=0,f\left(\phi \right)=0,\rho \left(\phi \right)=0$ ; (b) The time series of membrane potential under magnetic flow with $k_1=0.05,k_2=2,\alpha =2,\beta =0.0005$ ; (c) Fast/slow bifurcation analysis of bursting under the same parameter set as that of (a); (d) fast/slow bifurcation analysis of spiking under the same parameter set as that of (b)

图3. $g_K=20$ 神经元的放电模式及快慢分岔分析。(a) $I_{app}=0,f\left(\phi \right)=0,\rho \left(\phi \right)=0$ ，即不受磁流影响条件下膜电位的时间序列；(b) 磁流满足条件 $k_1=0.05,k_2=2,\alpha =2,\beta =0.0005$ 时的膜电位的时间序列；(c) 对应于图(a)的快慢分析；(d) 对应(b)的快慢分析

“fold/homoclinic”型簇放电，如图2(c)和图2(d)所示。

上述结果表明，在 $g_K=8.5$ 时，磁流没有改变簇放电的类型，但改变了簇放电的频率或周期。产生这一现象的主要原因是由于上支的稳定极限环和下支的稳定结点构成的双稳区域发生了改变，磁流作用使得双稳区域变小，从而簇放电的周期变小，频率增大。

当 $g_K=20$ 时，磁流作用使得神经元的放电模式由周期为2的簇放电转变为周期为1的峰放电，如图3(a)和图3(b)所示，对应的快慢分析分别如图3(c)和图3(d)所示。磁流作用使得神经元的放电周期变小，频率增大。同时，磁流作用使得双稳区域消失，此时只存在稳定的极限环吸引子(图3(d))，即神经元的放电模式为峰放电(图3(b))。也即，磁流作用使得神经元的放电模式由簇放电转变为峰放电。

4. 双参数分岔分析

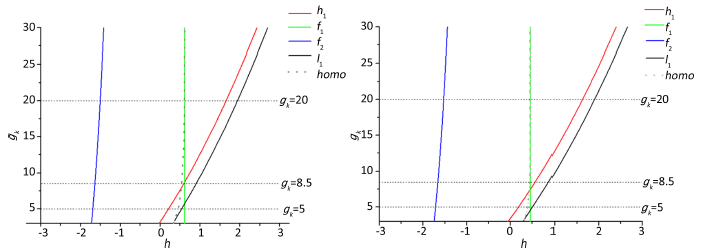
慢变参数h与钾离子电导 $g_K$ 的双参数分岔分析如图4所示，其中，红色的实线表示Hopf分岔曲线(h₁)，绿色实线以及蓝色实线表示鞍结分岔曲线 $\left(f_1,f_2\right)$ ，黑色实线表示极限环的鞍结分岔(l₁)，灰色虚线表示同宿轨分岔曲线(homo)。三条横虚线从下到上分别表示 $g_K$ 取5，8.5和20时的情形。在无磁流和磁流作用下，分岔曲线的相对位置基本类似。在 $g_K=5$ 附近，考察鞍结分岔曲线f₁和极限环的鞍结分岔曲线l₁相对位置。在无磁流的条件下， $g_K>5$ 时曲线f₁和曲线l₁相对位置发生改变；而在磁流作用下 $g_K<5$ 时这两条曲线f₁和l₁的相对位置发生改变。故而，在 $g_K=5$ 时，无磁流和在磁流作用下神经元的簇放电类型发生了转迁，如图1所示。当取 $g_K=8.5,20$ 时，f₁，l₁的相对位置没有发生变化。但加入磁流的神经元可以取稍小的值以达到未添加磁流的放电状态。

5. 结论

本文主要应用快慢变量分岔分析以及双参数分岔分析的方法，研究磁流对神经元放电模式的影响。当钾电导在一定参数范围变化时，Pre-Bӧtzinger复合体中兴奋性神经元呈节律性放电。研究表明，当 $g_k=5$ 时，磁流使得系统的簇放电从“subhopf/subhopf”型簇放电转变为“fold/homoclinic”型簇放电，这一转迁主要是由于平衡点的鞍结分岔曲线f₁和极限环的鞍结分岔曲线l₁的相对位置发生了改变。同时，在 $g_k$

(a) (b)

Figure 4. Two parameter bifurcation analysis of the fast subsystem in $\left(h,g_K\right)$ plane. (a) $I_{app}=0,f\left(\phi \right)=0,\rho \left(\phi \right)=0$ , discharge patterns of neuron are not affected by the magnetic flow; (b) $k_1=0.05,k_2=2,\alpha =2,\beta =0.0005$ , under the conditions of magnetic flow

图4. 快子系统在参数平面 $\left(h,g_K\right)$ 的双参数分岔。(a) $I_{app}=0,f\left(\phi \right)=0,\rho \left(\phi \right)=0$ ，即不受磁流影响；(b) 磁流满足条件 $k_1=0.05,k_2=2,\alpha =2,\beta =0.0005$

一定的情况下，磁流可以使得神经元的放电周期变小，频率增强。研究结果有助于揭示和解释电磁致病的动力学机理，为神经系统疾病的预防和治疗提供了一定的理论支持。

基金项目

本文得到国家自然科学基金(项目编号：11472009)，北方工业大学“科研创新团队建设计划”项目(项目编号：XN018010)，北方工业大学大学生科技活动的资助。

附录

在本文的模型中，对于 $x\in \left\{mP,m,h,n\right\}$ ，函数 $x_{\infty }\left(v\right)$ 可表示为 $x_{\infty }\left(v\right)={\left\{1+\exp \left[\left(v-{\theta }_x/{\sigma }_x\right)\right]\right\}}^{-1}$ 。对于 $x\in \left\{h,n\right\}$ ，函数 ${\tau }_x\left(v\right)={\tau }_x/\cosh \left[\left(v-{\theta }_x\right)/2{\sigma }_x\right]$ ，所用到的参数值见附表1。

Table 1. Parameter Values in Articles

附表1. 文章中的参数值