基于波动率状态转移的股票配资模型

Stock Loan Model under Volatility Regime Switching

摘要: 在股票波动率服从状态转移模型的假定下，利用期权定价原理建立股票配资问题的数学模型，同时使用有限差分方法进行求解。本文用数值算例说明配资炒股的收益和风险之间的关系，模型具有很好的实际应用价值。

Abstract: Under Volatility Regime Switching and by using option pricing theorem, this paper establishes a mathematical model for stock loan, and then uses finite difference method to solve it. Some nu-merical examples illustrate that the proposed model has good efficiency at the aspect of analyzing interest rate and risk rate.

1. 股票配资合同

杠杆炒股具有股票借贷的某些特征(见文献 [1] [2] )，也具有期权的一些基本要素(见文献 [3] [4] )，文 [5] 讨论了经典布朗运动下股票配资的数学模型，并从数值上分析了收益与风险之间的关系。在股票服从多状态转移假定下，本文采用Black-Scholes-Merton偏微分方程组对股票配资问题建模，同时设计有限差分格式求解，给出数值算例进行讨论。

设r为资本市场无风险利率， ${\sigma }_i,i=1,2,\cdots ,d$ 为某只股票价格在d个状态下的波动率，δ为分红强度，则股票价格 $S_t$ 服从随机微分方程(SDEs)

$\text{d}{S}_t\left(X_i\right)=\left(r-\delta \right)S_t\left(X_i\right)\text{d}t+{\sigma }_i{S}_t\left(X_i\right)\text{d}{W}_t,i=1,2\cdots ,d$ (1)

其中 $X_i$ 表示不同状态， $W_t$ 为标准Brownian运动。如果股民自己出资q，再从配资公司借贷kq买入一只股票，其股价正好为 $S=\left(1+k\right)q$ ，此时股票配资率(杠杆率)为 $1:k$ 。股民与配资公司订立下列合同条款：1) 借贷利率为γ，合同到期日为T，当前日期记为0。2) 如果在 $\left[0,T\right]$ 时间内，股票价格降至 $kq{\text{e}}^{\gamma t}$ ，股票自动平仓，股民资金全部亏损，配资公司收回本金与利息 $kq{\text{e}}^{\gamma t}$ 。3) 如果在 $\left[0,T\right]$ 时间内，股票价格升至 $\mu q$ ，股票自动平仓，配资公司收回本金与利息 $kq{\text{e}}^{\gamma t}$ ，股民资金收益为 $\mu q-kq{\text{e}}^{\gamma t}-q=\left(\mu -1\right)q-kq{\text{e}}^{\gamma t}$ 。这里总是假定 $\mu q>kq{\text{e}}^{\gamma T}+q$ ，设定μ的目的是防范估计被高估的风险，当股价高到一定程度时及时退出市场，股民和配资公司双方盈利。4) 在到期日，配资公司收回本金与利息 $kq{\text{e}}^{\gamma T}$ ，股民收入为 $S_T-kq{\text{e}}^{\gamma T}$ 。

2. 配资收益与风险模型

本文假定状态转移概率矩阵为

$A=\left[\begin{array}{cccc}-a_{11}& a_{12}& \dots & a_{1d}\\ a_{21}& -a_{22}& \dots & a_{2d}\\ ⋮& ⋮& \ddots & ⋮\\ a_{d1}& a_{d2}& \dots & -a_{dd}\end{array}\right],a_{ij}\ge 0$ , ${\displaystyle \underset{j=1,j\ne i}{\overset{d}{\sum }}{a}_{ij}}=a_{ii},i=1,2,\cdots ,d$

首先考虑收益模型。股民在到期日的收益支付函数可以看作股票看涨期权收益，即

$h\left(T,S_T\right)={\left(S_T-kq{\text{e}}^{\gamma T}-q\right)}^{+}$ ， ${(\cdot )}^{+}$ 表示取正部函数，而股民在任意t时刻的贴现收益期望为

$V_i\left(t,S_t\left(X_i\right)\right)=E^{t,S_t\left(X_i\right)}\left[{\text{e}}^{-r\left(T-t\right)}h\left(T,S_T\right)\right].$ (2)

在Black-Scholes-Merton分析框架上(见文献 [6] [7] )，股民收益期望 $V\left(t,S_t=S\right)$ 满足耦合偏微分方程组(PDEs)

$\begin{array}{l}\frac{\partial }{\partial t}{V}_i\left(t,S\right)+\left(r-\delta \right)S\frac{\partial }{\partial S}{V}_i\left(t,S\right)+\frac{1}{2}{\sigma }^2{S}^2\frac{{\partial }^2}{\partial S^2}{V}_i\left(t,S\right)-\left(r+a_{ii}\right)V_i\left(t,S\right)\\ +{\displaystyle \underset{j=1,j\ne i}{\overset{d}{\sum }}{a}_{ij}}{V}_j\left(t,S\right)=0,i=1,2,\cdots ,d\end{array}$ (3)

这里S为哑变量，不再是时间的随机函数。同时加上终端条件

$V_i\left(T,S\right)={\left(S-kq{\text{e}}^{\gamma T}-q\right)}^{+}.$ (4)

考虑到合同条款(2) (3)，我们必须加上边界条件

$V_i\left(t,kq{\text{e}}^{\gamma t}\right)=0,$ (5)

$V_i\left(t,\mu q\right)=\left(\mu -1\right)q-kq{\text{e}}^{\gamma t}.$ (6)

PDEs (3) (4) (5)和(6)构成多状态转移欧式看涨障碍期权。如果转移概率矩阵 $A=0$ ，状态转移模型退化为文 [7] 所描述的经典布朗运动模型。

再来讨论风险度量。股民在到期日的风险支付可以看作股票看跌期权收益，即

$\tilde{h}\left(T,S_T\right)={\left(q+kq{\text{e}}^{\gamma T}-S_T\right)}^{+}$ ，而股民在任意t时刻的贴现风险期望为

${\tilde{V}}_i\left(t,S_t\left(X_i\right)\right)=E^{t,S_t\left(X_i\right)}\left[{\text{e}}^{-r\left(T-t\right)}\tilde{h}\left(T,S_T\right)\right].$ (7)

与收益分析类似，股票风险期望 $\tilde{V}\left(t,S_t=S\right)$ 满足PDEs

$\begin{array}{l}\frac{\partial }{\partial t}{\tilde{V}}_i\left(t,S\right)+\left(r-\delta \right)S\frac{\partial }{\partial S}{\tilde{V}}_i\left(t,S\right)+\frac{1}{2}{\sigma }^2{S}^2\frac{{\partial }^2}{\partial S^2}{\tilde{V}}_i\left(t,S\right)-\left(r+a_{ii}\right){\tilde{V}}_i\left(t,S\right)\\ +{\displaystyle \underset{j=1,j\ne i}{\overset{d}{\sum }}{a}_{ij}}{\tilde{V}}_j\left(t,S\right)=0,i=1,2,\cdots ,d\end{array}$ (8)

和终端条件

${\tilde{V}}_i\left(T,S\right)={\left(q+kq{\text{e}}^{\gamma T}-S\right)}^{+}.$ (9)

考虑到合同条款(2) (3)，我们同样加上边界条件

${\tilde{V}}_i\left(t,kq{e}^{\gamma t}\right)=q,{\tilde{V}}_i\left(t,\mu q\right)=0.$ (10)

PDEs (8) (9) (10)构成所谓的欧式看跌障碍期权。如果已知零时刻股票价格 $S_0$ ，并给定配资率k，股

民投入资金数量 $q=\frac{1}{1+k}{S}_0$ ，此时股民在不同状态下的收益率I、风险率R和风险收益比λ可分别定义为

$I_i=V_i\left(0,S_0\right)/q,R_i={\tilde{V}}_i\left(0,S_0\right)/q,{\lambda }_i=\frac{{\tilde{V}}_i\left(0,S_0\right)}{V_i\left(0,S_0\right)},$ (11)

$I_i$ ， $R_i$ 和 ${\lambda }_i$ 都是无量纲的， $I_i$ 表示单位投入的收益， $R_i$ 表示单位投入的风险， ${\lambda }_i$ 则表示单位收益所面临的风险大小。 $I_i$ ， $R_i$ 和 ${\lambda }_i$ 对配资率k较为敏感，同时与借贷利率γ有关，应该是股民最为关注的数量指标。

计算收益期望的PDEs (3)~(6)可用有限差分方法来求解。定义固定时间网格

$\Delta t=T/M,t_m=m\Delta t,m=0,1,\cdots ,M$

和移动空间网格

$\Delta S^m=\left(\mu q-kq{\text{e}}^{\gamma t_m}\right)/N,S_n^m=kq{\text{e}}^{\gamma t_m}+n\Delta S^m,n=0,1,\cdots ,N.$

记 $V_{m,n}^i$ 为期权价值 $V_i\left(t,S\right)$ 在状态 $X_i$ ，时刻 $t_m$ 和股价为 $S_n^m$ 时的数值解。运用中心差分的隐式格式离散PDE (3)得到

$\begin{array}{l}\frac{{\hat{V}}_{m,n}^i-V_{m-1,n}^i}{\Delta t}+\left(r-\delta \right)S_n^{m-1}\frac{V_{m-1,n+1}^i-V_{m-1,n-1}^i}{2\Delta S^{m-1}}+\frac{1}{2}{\sigma }^2{\left(S_j^{m-1}\right)}^2\frac{V_{m-1,n+1}^i-2V_{m-1,n}^i+V_{m-1,n-1}^i}{{\left(\Delta S^{m-1}\right)}^2}\\ -\left(r+a_{ii}\right)V^i{}_{m-1,n}+{\displaystyle \underset{j=1,j\ne i}{\overset{d}{\sum }}{a}_{ij}}{V}_{m-1,n}^j=0,m=M,M-1,\cdots ,1;n=1,2,\cdots ,N-1.\end{array}$ (12)

其中 ${\hat{V}}_{m,n}^i$ 为 $V_{m,n}^i$ 在时间层 $t_{m-1}$ 上的插值函数。对离散系统(12)进行整理，依次关于时间节点 $m=M,M-1,\cdots ,1$ 有

$\begin{array}{l}{p}_{i,m-1,n}{V}_{m-1,n-1}^i+q_{i,m-1,n}{V}_{m-1,n}^i+c_{i,m-1,n+1}{V}_{m-1,n}^i\\ +{\displaystyle \underset{j=1,j\ne i}{\overset{d}{\sum }}{l}_{i,j}}{V}_{m-1,n}^j={\hat{V}}_{m,n}^i,m=1,2,\cdots ,N-1,\end{array}$ (13)

其中

$\begin{array}{l}{p}_{i,m-1,n}=\left(r-\delta \right)S_n^{m-1}\Delta t-\frac{{\sigma }_i^2{\left(S_n^{m-1}\right)}^2\Delta t}{2{\left(\Delta S^{m-1}\right)}^2},\\ q_{i,m-1,n}=1+\frac{{\sigma }_i^2{\left(S_n^{m-1}\right)}^2\Delta t}{{\left(\Delta S^{m-1}\right)}^2}+\left(r+a_{ii}\right)\Delta t,\\ c_{i,m-1,n}=-\left(r-\delta \right)S_n^{m-1}\Delta t-\frac{{\sigma }_i^2{\left(S_n^{m-1}\right)}^2\Delta t}{2{\left(\Delta S^{m-1}\right)}^2},l_{i,j}=a_{ij}\Delta t.\end{array}$

加上终端条件和边界条件

$V_{M,n}^i={\left(S_n^M-kq{\text{e}}^{\gamma T}-q\right)}^{+},V_{m-1,0}=0,V_{m,N}=\left(\mu -1\right)q-kq{\text{e}}^{\gamma t_m},$

线性方程组(13)可按时间反向演化求解。如果令矩阵和向量

$\begin{array}{l}{B}_i=Diag\left(p_{i,m-2,n},q_{i,m-2,n},c_{i,m-2,n}\right),\\ f_i={\left[{\hat{V}}_{m,1}^i,{\hat{V}}_{m,2}^i,\cdots ,{\hat{V}}_{m,N}^i-\left(\mu -1\right)q-kq{\text{e}}^{\gamma t_m}\right]}^{\text{T}}\end{array}$

则离散方程(13)有矩阵形式

同理计算风险期望的PDE (8)~(11)也可用有限差分方法来求解，方法类似，这里不再赘述。

3. 数值模拟与分析

考虑两个状态的情形，取无风险利率 $r=0.05$ (年利率)，股价波动率 ${\sigma }_1=0.1,{\sigma }_2=0.4$ ，初始股价 $S_0=10$ (元)，借贷利率 $\gamma =0.07$ ，到期时间 $T=1$ (年)，其它参数为 $q=S_0/\left(1+k\right)$ ， $\mu =6$ ， $M=1000$ ， $N=1000$ 。

表1列出了有限差分方法的部分计算结果，图1显示了两个不同状态下的收益率、风险率和风险–收益比。从中看到，随着配资率k的增加，单位资本的收益(R)先增后降；在较低配资水平下确实能增加股民期望收益，这正是股民涉足场外配资炒股的动力所在；但在较高配资水平下，由于面临高额借贷利息，股民期望收益必然受损。同时我们也看到，随着配资率k的增加，单位资本的风险( $\tilde{R}$ )先增后降；高配资高风险不难理解；配资水平达到一定程度以后，股民投入很少，风险自然会减低，其余风险已经转嫁给配资公司。单位收益所面临的风险λ总是在提高，这说明风险增长速度快于收益增长速度。另外从表中我们也能看到高收益高风险的投资特征。

Table 1. Impact of interest and risk for different allocation rate

表1. 不同配资率对收益和风险的影响

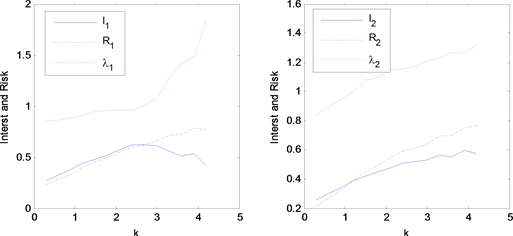
Figure 1. Impact of interest and risk for different allocation rate. Left sub-figure for regime-1 and right sub-figure for regime-2

图1. 不同配资率对收益和风险的影响，左图为状态-1，右图为状态-2

从以上分析看出，本文提出的股票配资模型基本体现了借贷炒股的主要特征，实际数值计算结果能够给出股民最为关心的数量指标，具有很强的实用价值。

基金项目

2016年度湖南省大学生研究性学习和创新性实验计划项目。