1. 引言
软件成本预测是软件开发中重要的步骤之一,灰色模型和一元线性回归模型是软件成本预测中常用的预测模型。灰色模型是邓聚龙教授提出的灰色系统理论中的重要内容,灰色系统理论是针对小样本、贫信息的不确定系统进行研究,在医学、教育、工业、军事等领域有着广泛的应用 [1] 。线性回归是最基本和应用最广泛的预测方法。灰色理论在被提出后的三十多年来经过了快速成长与发展,线性回归模型是受到普遍认可的成熟模型,如果能在这两个模型上找到共通点,能够增强对灰色模型内在机理的了解,有助于灰色模型的普及。
在使用灰色模型建模时,为了提高预测模型的精度,人们一直在致力于研究新的建模技术和改进方法,研究表明,原始数据的模式及光滑性是影响灰色模型精度的两个主要因素 [2] ,所以为了提高模型的模拟和预测精度,会对模型采取一些处理措施,如文献 [3] 。对原始序列进行平移变换是其中的处理方法之一。平移变换即在建模之前,对原始序列的每一个数据加上一个数,构造一个新的序列,再对新的序列进行建模 [4] 。对单调递增数列进行平移变换,会使变换后数列的光滑性增强 [5] ,进而影响模型的预测误差,这是平移变换的核心作用。文献 [4] [5] [6] 中探讨了平移变换对数据建模的作用,得出平移变换可以提升模型的性能的结论。
作为灰色模型和线性回归模型中最典型的模型,近年来将GM(1,1)模型和一元线性回归模型一起讨论的学者也很多。包括将两种模型结合起来进行数据的预测,弥补各自的缺点,能得到比较好的效果 [7] ,或者单纯比较两种模型的建模效果。但是将平移变换后的GM(1,1)模型与一元线性回归模型进行比较并研究两者内在联系的研究还未发现。
本文是对灰色模型中的GM(1,1)模型和一元线性回归模型相关性的研究,揭示了应用平移变换后的GM(1,1)模型与一元线性回归模型有着高度的一致性,换句话说,平移变换可以将GM(1,1)模型从某种意义上转化为一元线性回归模型,从而把两种模型在一定程度上统一起来,使灰色模型更易于让人理解和接受,对灰色系统理论的推广有积极的意义。本文将在第二节中阐述本文研究的问题、实验步骤和所用的检验方法。接下来通过实验得出结果,分析结果并得出最后的结论。
2. 研究问题与方法
2.1. 研究问题
实验发现,对经过平移变换的原始序列建立GM(1,1)模型,随着平移量的增加,模拟序列曲线会趋于平直,最后基本成为一条直线。因此我们想要研究,与图形为一条直线的一元线性回归模型相比较,两种模型所得的建模结果有什么内在联系,随着平移量的增加,两者之间的联系会有什么变化。
2.2. 实验步骤
研究平移变换后GM(1,1)模型和一元线性回归模型相似性的步骤如下:
1) 准备实验数据集,对数据进行分组,整理成所需的原始序列集。
2) 对原始序列进行平移变换。
3) 对原始序列构建一元线性回归模型,对每次平移后得到的新序列分别构建GM(1,1)模型。
4) 对每一组GM(1,1)模型的模拟值与对应的一元线性回归模型的模拟值进行比较。
5) 分析随平移量的变化,两种模型的相似性的变化趋势,并得出结论。
2.3. 检验方法
本文在对原始序列进行平移变换后建立GM(1,1)模型的建模结果和一元线性回归模型建模结果进行比较时,采用两种方法进行研究:
1) 对平移变换后的GM(1,1)模型所得数据与一元线性回归模型所得数据进行配对样本T检验,每平移一次进行一次检验,如果验证每次平移后,配对样本T检验所得的 值均大于0.05,说明两种模型的结果不存在显著差异,来自一个总体,具有相似性。
2) 对两组实验数据进行差异度量。两组数据之间的差异可以用偏差和来表示。将GM(1,1)模型每次平移后所得的结果分别与一元线性回归模型所得的结果作差并取绝对值,将每组结果的差值绝对值相加,若差值绝对值和越小,则说明两组数据越接近,反之,两组数据的差距越大。
3. 实验与分析
3.1. 平移变换对GM(1,1)模型的作用
我们首先用一组数据来验证原始序列进行平移变换后,对GM(1,1)模型建模结果的影响。
设X(k)为原始序列,
。在建模之前,首先对原始序列进行光滑性检验。经检验,所得的光滑比为:
当k > 3时,光滑比均大于0.5,准光滑性条件不满足。
对原始序列进行平移变换是使其变光滑的一种手段。对原始序列平移10次,每次平移的量分别为0,2,4,8,16,32,64,128,256,512。第一次平移量为0,即平移后序列
与原始序列X相同,第二次平移量为2,依次类推。得到10组新的序列为:
对平移后的10组新序列进行光滑性检验,发现前3组数据,即平移量为0,2,4时的
,仍不满足准光滑性条件;当进行第4次平移,即平移量达到8时,序列
所得的光滑比在
时,光滑比均小于0.5,准光滑性条件满足。此后的平移数组准光滑性也均满足。
尽管前三个序列不满足光滑性条件,仍可应用GM(1,1)模型得到建模结果,为了更清楚地看到平移变换后序列建模的变化趋势,我们保留前三组,用全部10组序列构建GM(1,1)模型。
对
到
10组序列进行GM(1,1)模型的构建,得到的10次建模的曲线如图1所示。
由图1首先可以看出,GM(1,1)模型建模后的第一个点不变,一直都与原始序列的第一个点相同。从曲线的形状来看,平移量为0时所得的GM(1,1)模型原始曲线比较弯曲,随着平移量的增加,所得曲线弯曲的弧度变小,逐渐变得平直,进行到最后一次平移时,第二到第六个点的曲线几乎成为一条直线。那我们就将这最后一次平移的曲线与一元线性回归模型曲线进行对比,探究两种模型之间的联系。
序列X构建一元线性回归模型所得模拟值为
。GM(1,1)模型最后一次平移所得结果为
。两组数据所得图像如图2。
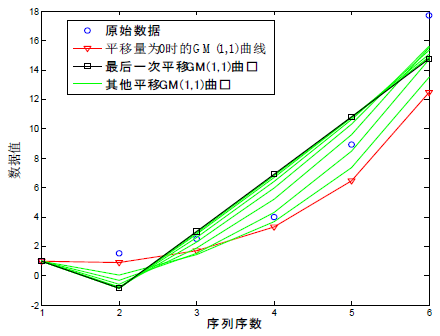
Figure 1. Curve: 10 translations of original sequence of GM(1,1) model
图1. 原始序列10次平移后建立GM(1,1)模型曲线
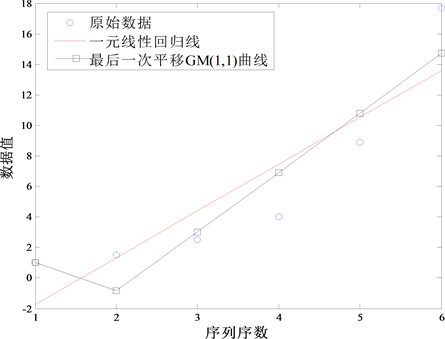
Figure 2. Curve: The last translational GM (1,1) model and one linear regression model
图2. GM(1,1)模型与一元线性回归模型比较曲线
如图2所示,虽然经过平移变换后的GM(1,1)模型曲线第二到第六个点部分几乎为一条直线,但与一元线性回归模型的曲线并不重合。
这是因为,在GM(1,1)模型中,原始序列第一个点虽然在建模中也进行了模拟,但是从图1中发现,在模拟序列中,第一个点始终和原始序列中的点重合,并没有发生变化,而一元线性回归模型的所有点都发生了变化。既然GM(1,1)模型中原始序列的第一个点对模拟序列没有影响,那么构建一元线性回归模型时,我们可以去掉原始序列X的第一个点,用其余各点构建模型。因此,在本实验中,构建一元线性回归模型时使用原始序列的第二至六个点,构建GM(1,1)模型时使用原始序列的全部数据。此时得到的一元线性回归建模结果为
,与最后一次平移的GM(1,1)模型图像如图3所示。
如图所示,当去掉原始序列的第一个点再构建一元线性回归模型时,一元线性回归模型的曲线与GM(1,1)模型后五个点组成的曲线从观察上完全重合了。
但是因为本实验只使用了一组原始序列数据,无法确定这个结果是否是普遍规律,即无论对什么类型的原始序列,经过足够大的平移变换后,用GM(1,1)模型建模,得到的模型曲线就会与一元线性回归曲线重合?为此,我们选用更多的数据,进行系统的实验来证明这个发现。
3.2. 原煤产量实验
为了确定上节构造序列进行的实验是否具有普遍性,本节我们使用现实世界的真实数据进行探究。在国家统计局网站年度数据中,选取了1998年至2014年17年的原煤年产量数据,由此得到由17个原始数据组成的原始序列为:
。
上节实验原始序列长度为6,事实上,我们可以在原始序列上建立其他长度的灰色模型,同样,我们也关心在不同长度的序列上,前述发现是否同样存在。在本实验中,我们将建立长度分别为5、6、8、10的序列。由于原始数据数量较少,为得到更多的数据进行实验,我们采用重叠分组的方式:以原始序列长度等于6为例,把第1至6个数据分为一组,第2至7个数据为一组,以此类推,直到第12至17个
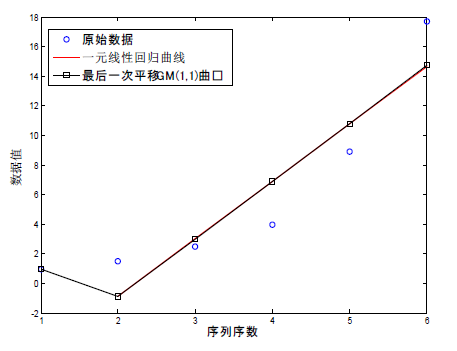
Figure 3. Curve: GM(1,1) model and simple linear regression model for no first point
图3. 无第一个点时GM(1,1)模型与一元线性回归模型曲线
数据为一组,共分成了12组,每组6个数据。
验证数据符合光滑性检验后,按照3.1节中的方法,对每组数据进行平移,平移量依然为0,2,4,8,16,32,64,128,256,512。
因为本次实验数据量相对较多,可以使用配对样本T检验和差异度量的方法检验两种模型模拟值的关系,以此来进行定量评估。
使用SPSS软件对每组数据每次平移所得的GM(1,1)模型模拟数据与一元线性回归模型模拟数据进行配对样本T检验,4次分组分别进行配对样本T检验所得P值如表1所示。
由表1得知,10次平移的GM(1,1)模型模拟值与一元线性回归模型模拟值进行配对样本T检验,所得的P值均大于0.05,此时不能拒绝原假设,即两种模型的数据不存在显著差异,说明原始序列经过平移变换后建立的GM(1,1)模型与一元线性回归模型具有相似性。
下面用差异度量方法进行检验。得出的两个模型模拟值差值绝对值如下表2所示。

Table 1. P value of paired sample T test
表1. 配对样本T检验P值

Table 2. The difference measure of 4 subgroups of the output of raw coal
表2. 原煤产量4次分组两模型差值绝对值和
由上表可以看出,不论对原始数据如何分组,所得的实验规律都是相同的,即随着平移量的增加,GM(1,1)模型和一元线性回归模型模拟值的差值均减小。
根据表2的差值绝对值之和,按平移量作折线图,如图4所示。
折线图直观地显示出了原始数据进行平移变换后构建GM(1,1)模型的模拟值与一元线性回归模型模拟值差值绝对值和的变化趋势。曲线呈下降趋势,说明随平移量的增加,差值越来越小,逐渐接近于0,即GM(1,1)模型愈加接近一元线性回归模型。除此之外,也使用了其他多组真实数据进行了实验,所得结果与以上实验相同。因此,我们可以说,对原始序列进行平移变换,随平移量的增加,构建GM(1,1)模型所得的模拟值,与在第二个点后构建一元线性回归模型的模拟值会越来越接近,这一结论对不同类型和不同长度的序列均适用。
4. 总结
本文发现了原始序列经过平移变换后构建的GM(1,1)模型以及去掉第一个数据后构建的一元线性回归模型,两种模型所得的结果会随着平移量的增加而逐渐接近乃至重合,并通过1998年至2014年17年
 (a) 5个数据一组
(a) 5个数据一组 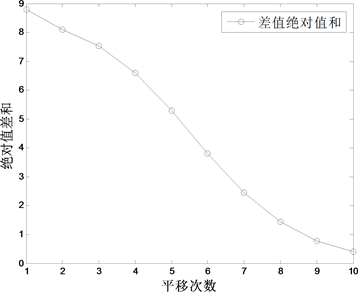 (b) 6个数据一组
(b) 6个数据一组  (c) 8个数据一组
(c) 8个数据一组  (d) 10数据一组
(d) 10数据一组
Figure 4. The difference measure of 4 subgroups of the output of raw coal
图4. 原煤产量4次分组两模型差值绝对值和
的原煤年产量数据进行实验证明这一观点。这说明平移变换可以使GM(1,1)模型转化为一元线性回归模型。因为线性回归模型的简单性,这两种模型间联系的发现有利于帮助进一步认识GM(1,1)模型的本质,对灰色模型的理论发展和推广传播有积极意义。