1. 引言
随机变量序列完全收敛能推导出几乎必然收敛,几乎必然收敛能推导出依概率收敛 [1] 。目前有大量文章研究相依随机变量序列的收敛性问题,文献 [2] [3] 研究了有关混合序列加权和的完全收敛性,文献 [4] [5] [6] 研究了混合序列加权和的几乎必然收敛性。而对于一般的随机变量序列,文献 [7] 在研究几乎必然收敛时考虑了以单调递减趋于0的实数数列,得到判断几乎必然收敛的一个等价条件。
本文在研究随机变量序列的收敛性时,考虑了单调递减趋于0的实数数列。在考虑以单调递减趋于0的实数数列应用到完全收敛性的判断中,得到了判断完全收敛的一个等价条件,同时研究了完全收敛性判断的两个充分条件。这些研究都是针对一般的随机变量序列,没有独立性或同分布的要求。并且用简单的例子说明了这些条件之间的相互关系。
2. 随机变量序列收敛定义及相关定理
首先给出随机变量序列几种收敛的定义。
定义2.1 ( [1] ) 随机变量序列
依概率收敛到随机变量X,当且仅当下式成立
(1)
简记为
。
定义2.2 ( [1] ) 随机变量序列
几乎必然收敛到随机变量X,当且仅当下式成立
(2)
简记为
。
定义2.3 ( [1] ) 随机变量序列
完全收敛到随机变量X,当且仅当下式成立
(3)
简记为
。
三种收敛性之间的关系是( [1] )
下面定理 2.1 给出了几乎必然收敛的一些等价条件。
定理2.1 ( [1] )
与下面每个式子等价
(4)
(5)
(6)
(7)
(8)
令正实数序列
单调递减以 0 为极限,容易证明下面关系式成立
由上式即得到下面的推论
推论2.2
与下面三个式子均等价
(9)
(10)
(11)
注2.1 当取
时,(9)式即为(6)式,(10)式即为(7)式,(11)式即为(8)式。
考虑单调递减趋于0的实数数列,文献 [7] 给出了几乎必然收敛另外的等价条件。
定理2.3 ( [7] )
等价于
(12)
值得注意的是,(12)式中随机变量序列
的下标和正实数序列
的下标有直接的关系,这不同于上面推论2.2中的三个式子。
由概率的连续性即得到
与下面式子等价
(13)
3. 主要结果及证明
如同几乎必然收敛的判定一样,在完全收敛的判定中引入单调递减趋于0的实数数列,得到下面的定理。
定理3.1 对随机变量序列
及随机变量X,有
与下式等价
(14)
证“⟸”:因为存在使(14)式成立的数列
,
,所以对任意
,必存在N,当
时,
。由此得当
时,
,有
得
。
“⟹”:若
,取实数序列
,
,则对
,有
又因为
所以存在正整数
,使得
所以有
同理,对
,存在正整数
,使得
对
,存在正整数
,且满足
,使得
所以
令
,有
对每个
,当
时,取这些
。由此得
,而且满足
。 □
由Borel-Cantelli引理知
,但
,如下例。
例3.1 设
是独立同分布的随机变量序列,
服从双边Pareto分布,其密度函数为
则
,
,
。令
,由Kolmogorov强大数定律( [1] , p. 295),
且
;由Hsu-Robbins-Erdos强大数定律( [1] ,p312),
且
。由此知
,但 不成立。
不成立。
由(5)式知
,但
,如下面的例子。
例3.2 令随机变量
的分布为
,
,则对
,有
当
,得
。然而当随机变量序列
相互独立时,对任意
,
由Borel-Cantelli引理知
不成立。
下面的命题3.2和3.3是两个很强的条件。
命题3.2 设有随机变量序列
及随机变量X,若
(15)
则 。简记为
。
。简记为
。
证 因
所以
. □
易知(15)式⟺
,因从右推出左是显然的。
若对任意n,下式成立
(16)
则容易知道(16)式比(15)式给的条件稍弱,因
时,
,所以(15)式⟹(16)式。然而(16)式⇏(15)式,如下面的例3.3。
例3.3 令随机变量
的分布为
,
。令 ,正实数序列
取为
,则有(16)式成立。但对任意的正实数序列
单调递减以0为极限,知当
时,
;当
时,
。对任意给定n必有某些
,所以(15)式不成立。
,正实数序列
取为
,则有(16)式成立。但对任意的正实数序列
单调递减以0为极限,知当
时,
;当
时,
。对任意给定n必有某些
,所以(15)式不成立。
上面直接由
的分布容易得到
,因对样本空间中任意
,有
,所以
。
下面命题说明(16)式比完全收敛的条件更强。
命题3.3 设有随机变量序列
及随机变量X,若(16)式成立,则(3)式成立。
证 因存在使(16)式成立的数列
,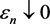 ,所以对任意
,必存在N,当
时,
,由此得到
,所以对任意
,必存在N,当
时,
,由此得到
得(3)式成立。
由命题3.3知,(16)式成立可得(3)式成立,从而
。不过也很容易地由(16)式直接得到
。因对任意
,存在N,使得当
时,
,所以当
时
从而
得(5)式成立,所以有
。
由命题3.3知,(16)式⟹(3)式,但(3)式⇏(16)式,如下面的例3.4。
例3.4 设有随机变量序列
,其中
的分布律为
则对任意
,有
所以(3)式成立。然而对任意的正实数序列
单调递减以0为极限,存在N,当
时,
。所以当
时,
。由此得(16)式不成立。
由以上命题,有如下结论
⟺(15)⇒(16)⇒(14)⟺
⇒
⟺(12)⇒
而且举例说明了上面蕴含关系的相反方向不成立。