纳米尺度下半空间内浅埋圆形弹性夹杂对SH波的散射

Scattering of a Nanoscale Circular Elastic Inclusion on SH Wave in a Semi-Space

摘要: 本文利用复变函数法、多极坐标法、虚源法和Graf加法公式研究了在纳米尺度下含有圆形夹杂的弹性半空间对SH波的散射问题。首先根据边界条件求出了介质内的入射、反射、散射、折射波函数，然后利用波函数求出在复数坐标系下相对应的应力场，最后，给出了界面圆形夹杂的动应力集中的算例和结果。具体讨论了圆孔夹杂边界处的环向动应力随无量纲波数、入射角变化时的变化情况，以及分析了表面参数S对动应力集中的影响，比较了在宏观和微观下的动应力集中。结果表明：在纳米尺度下，表面参数越小，引起的圆形夹杂边界处的应力集中程度越强；无量纲波数越大，引起的圆形夹杂边界处的应力集中程度越强。

Abstract: Using complex function method, multi-polar coordinate method, image-source method, and Graf’s addition formula, the scattering of SH wave by a nano-circular inclusion in elastic half space was studied. Firstly, according to the boundary conditions, the reflected, scattered and refracted wave functions in medium were calculated. Then the wave functions of the corresponding stress field in complex coordinate system were derived. Finally, the calculation examples and results of the dynamic stress concentration around the interface of the circular inclusion were presented in the paper. The variation of circumferential dynamic stress around the boundary of circular inclusion with dimensionless wave number and the change of incidence angle were discussed in detail. The researcher also analyzed the influence of surface parameters on dynamic stress concentration and compared the dynamic stress concentration under macroscopic and microscopic conditions. The results show that the stress concentration at the boundary of the circular inclusion is stronger with the smaller the surface parameter and the higher the dimensionless wave number.

1. 引言

弹性波在固体中传播时，固体中嵌有的夹杂(孔洞)会引发弹性波的散射，进而产生动应力集中。对此Mow和Pao [1] [2] 研究了无限大平面内一个夹杂(孔洞)对平面弹性波的散射问题。史守峡和刘殿魁 [3] 探讨了多圆孔对SH波的散射及动应力集中，分析了多圆孔干涉现象。由于受到平界面的影响，林宏和刘殿魁 [4] 继续研究了半无限空间中圆孔周围SH波的散射。史文谱等人 [5] 则为了探究平表面和弹性夹杂对弹性波的干涉，研究了弹性约束半空间内浅埋圆孔对SH波的散射。齐辉，杨在林 [6] [7] [8] [9] 等研究了夹杂(孔洞)对SH波散射的应用。

随着夹杂尺寸的减少，尤其是在纳米尺度下，由于比表面积显著增加，以及表面原子和内部原子巨大的势能差，表面效应显著，使得纳米材料和纳米元器件的动力学性能同宏观性能明显不同。近年来，汝艳 [10] [11] 等研究了SH波诱发的阵列纳米孔洞周围的弹性波散射和动应力集中以及Wang [12] 探讨了多个圆形纳米夹杂(孔洞)对P波的散射问题。本文利用复变函数法、多极坐标法、虚源法和Graf加法公式，研究了在纳米尺度下半空间内浅埋圆形夹杂对稳态入射平面SH波的散射，以及由此引起的动应力集中。

2. 问题模型和分析

如图1所示，纳米尺度的半空间介质内有一个圆形弹性夹杂，其掩埋深度为H，半径为R，剪切模量为 ${\mu }_i$ ，质量体密度为 ${\rho }_i$ ，半空间介质的剪切模量为 $\mu$ ，质量体密度为 $\rho$ 。建立如图所示的直角坐标系 $xoy$ 和 $x_1{o}_1{y}_1$ 。假设半空间直边界为 ${\Gamma }_H$ ，圆形弹性夹杂边界为 ${\Gamma }_R$ ，一列稳态入射平面SH波 $W^{\left(\text{I}\right)}$ (入射波函数)以入射角 $\alpha$ 在介质内传播，并与半空间直边界和圆形弹性夹杂边界发生作用，在半空间内产生反射波 $W^{\left(\text{r}\right)}$ 和散射波 $W^{\left(\text{s}\right)}$ ，以及在圆形弹性夹杂中产生折射波 $W^{\left(\text{f}\right)}$ 。这些波函数都满足Helmholtz方程

${\nabla }^{2}W+K^{2}W=0$ (1)

其中， ${\nabla }^2=\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2}$ 是拉普拉斯算子； $k=\frac{\omega }{V}$ 是波数， $\omega$ 是圆周频率， $V=\sqrt{\frac{\mu }{\rho }}$ 为波速，W为介质内的位移场，在这里直接将稳态时间因子 ${\text{e}}^{-i\omega t}$ 忽略了。

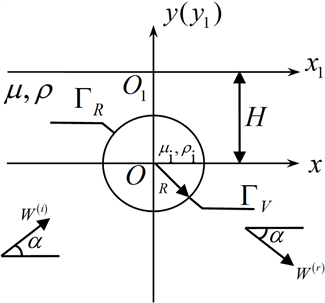
Figure 1. Scattering of a shallow buried circular inclusion in a half space for a steady incident plane SH wave

图1. 半空间内浅埋圆形夹杂对稳态入射平面SH波的散射

在弹性力学中，剪切应力 ${\tau }_{rz}$ 和 ${\tau }_{\theta z}$ 与位移的关系为

$\{\begin{array}{l}{\tau }_{rz}=\mu \left(\frac{\partial W}{\partial z}{\text{e}}^{i\theta }+\frac{\partial W}{\partial \bar{z}}{\text{e}}^{-i\theta }\right)\\ {\tau }_{\theta z}=i\mu \left(\frac{\partial W}{\partial z}{\text{e}}^{i\theta }-\frac{\partial W}{\partial \bar{z}}{\text{e}}^{-i\theta }\right)\end{array}$ (2)

其中， $z=r{\text{e}}^{i\theta }$ ， $\bar{z}=r{\text{e}}^{-i\theta }$ ；i为虚数单位， $i^2=-1$ ； ${\tau }_{rz}$ 和 ${\tau }_{\theta z}$ 分别是反平面问题中的径向面和环向面的剪切应力。

入射波函数

$W^{\left(\text{I}\right)}=W_0{\text{e}}^{\frac{ik}{2}\left[\left(z{\text{e}}^{-i\alpha }+\bar{z}{\text{e}}^{i\alpha }\right)\right]{\text{e}}^{-iHk\sin \alpha }}$ (3)

反射波函数

$W^{\left(\text{r}\right)}=W_0{\text{e}}^{\frac{ik}{2}\left[\left(z{\text{e}}^{-i\alpha }+\bar{z}{\text{e}}^{i\alpha }\right)\right]{\text{e}}^{iHk\sin \alpha }}$ (4)

利用虚源法可以得到散射波函数

$W^{\left(\text{s}\right)}={\displaystyle \underset{n=-\infty }{\overset{\infty }{\sum }}{A}_n\left\{H_n^{\left(1\right)}\left(k\left|z\right|\right){\left(\frac{z}{\left|z\right|}\right)}^n+H_n^{\left(1\right)}\left(k\left|z-2Hi\right|\right){\left(\frac{z-2Hi}{\left|z-2Hi\right|}\right)}^{-n}\right\}}$ (5)

折射波函数为

$W^{\left(\text{f}\right)}={\displaystyle \underset{n=-\infty }{\overset{\infty }{\sum }}{B}_n{J}_n}\left(k_i\left|z\right|\right){\left(\frac{z}{\left|z\right|}\right)}^n$ (6)

其中， $W_0$ 为入射波振幅， $A_n,B_n\left(n=0,n=\pm 1,n=\pm 2,\cdot \cdot \cdot \right)$ 是待定的系数， $H_n^1(\cdot )$ 表示n阶第一类Hankel函数， $J_n(\cdot )$ 表示n阶第一类贝塞尔函数。

将方程(3)代入方程(2)，求出入射波对应的应力分别为

${\tau }_{rz}^{\left(\text{I}\right)}=\frac{\text{i}k\mu W_0}{2}\left[{\text{e}}^{i\left(\theta -\alpha \right)}+{\text{e}}^{-i\left(\theta -\alpha \right)}\right]{\text{e}}^{-iHk\sin \left(\alpha \right)}{\text{e}}^{\frac{ik}{2}\left(z{\text{e}}^{-i\alpha }+\bar{z}{\text{e}}^{i\alpha }\right)}$ (7)

${\tau }_{\theta \text{z}}^{\left(\text{I}\right)}=\frac{-k\mu W_0}{2}\left[{\text{e}}^{i\left(\theta -\alpha \right)}+{\text{e}}^{-i\left(\theta -\alpha \right)}\right]{\text{e}}^{-iHk\sin \left(\alpha \right)}{\text{e}}^{\frac{ik}{2}\left(z{\text{e}}^{-i\alpha }+\bar{z}{\text{e}}^{i\alpha }\right)}$ (8)

将方程(4)代入方程(2)，求出反射波对应的应力场分别为

${\tau }_{rz}^{\left(\text{r}\right)}=\frac{\text{i}k\mu W_0}{2}\left[{\text{e}}^{i\left(\theta \text{+}\alpha \right)}+{\text{e}}^{-i\left(\theta \text{+}\alpha \right)}\right]{\text{e}}^{iHk\sin \left(\alpha \right)}{\text{e}}^{\frac{ik}{2}\left(z{\text{e}}^{i\alpha }+\bar{z}{\text{e}}^{-i\alpha }\right)}$ (9)

${\tau }_{\theta z}^{\left(\text{r}\right)}=\frac{-k\mu W_0}{2}\left[{\text{e}}^{i\left(\theta \text{+}\alpha \right)}-{\text{e}}^{-i\left(\theta \text{+}\alpha \right)}\right]{\text{e}}^{iHk\sin \left(\alpha \right)}{\text{e}}^{\frac{ik}{2}\left(z{\text{e}}^{i\alpha }+\bar{z}{\text{e}}^{-i\alpha }\right)}$ (10)

将方程(5)代入方程(2)，求出散射波对应的应力场分别为

$\begin{array}{c}{\tau }_{rz}^{\left(\text{s}\right)}=\frac{k\mu }{2}{\displaystyle \underset{n=-\infty }{\overset{\infty }{\sum }}{A}_n[H_{n-1}^{\left(1\right)}\left(k\left|z\right|\right){\left(\frac{z}{\left|z\right|}\right)}^{n\text{-}1}{\text{e}}^{i\theta }-H_{n\text{+}1}^{\left(1\right)}\left(k\left|z\right|\right){\left(\frac{z}{\left|z\right|}\right)}^{n+1}{\text{e}}^{-i\theta }}\\ -H_{n+1}^{\left(1\right)}\left(k\left|z-2Hi\right|\right){\left(\frac{z-2Hi}{\left|z-2Hi\right|}\right)}^{-n-1}{\text{e}}^{i\theta }+H_{n-1}^{\left(1\right)}\left(k\left|z-2Hi\right|\right){\left(\frac{z-2Hi}{\left|z-2Hi\right|}\right)}^{-n+1}{\text{e}}^{-i\theta }]\end{array}$ (11)

$\begin{array}{c}{\tau }_{\theta z}^{\left(\text{s}\right)}=\frac{\text{i}k\mu }{2}{\displaystyle \underset{n=-\infty }{\overset{\infty }{\sum }}{A}_n[H_{n-1}^{\left(1\right)}\left(k\left|z\right|\right){\left(\frac{z}{\left|z\right|}\right)}^{n\text{-}1}{\text{e}}^{i\theta }+H_{n\text{+}1}^{\left(1\right)}\left(k\left|z\right|\right){\left(\frac{z}{\left|z\right|}\right)}^{n+1}{\text{e}}^{-i\theta }}\\ -H_{n+1}^{\left(1\right)}\left(k\left|z-2Hi\right|\right){\left(\frac{z-2Hi}{\left|z-2Hi\right|}\right)}^{-n-1}{\text{e}}^{i\theta }-H_{n-1}^{\left(1\right)}\left(k\left|z-2Hi\right|\right){\left(\frac{z-2Hi}{\left|z-2Hi\right|}\right)}^{-n+1}{\text{e}}^{-i\theta }]\end{array}$ (12)

将方程(6)代入方程(2)，求出折射波对应的径向应力场为

${\tau }_{rz}^{\left(\text{f}\right)}=\frac{k_i{\mu }_i}{2}{\displaystyle \underset{n=-\infty }{\overset{\infty }{\sum }}{B}_n\left[J_{n-1}\left(k_i\left|z\right|\right){\left(\frac{z}{\left|z\right|}\right)}^n+J_{n+1}\left(k_i\left|z\right|\right){\left(\frac{z}{\left|z\right|}\right)}^n\right]}$ (13)

弹性夹杂外内的总波场 $W^{\left({\text{t}}_1\right)}$ 、 $W^{\left({\text{t}}_2\right)}$ 以及总应力场 ${\tau }_{rz}^{\left({\text{t}}_1\right)}$ 、 ${\tau }_{\theta z}^{\left({\text{t}}_1\right)}$ 、 ${\tau }_{rz}^{\left({\text{t}}_2\right)}$ 场依据叠加原理可表示为

$W^{\left({\text{t}}_1\right)}=W^{\left(\text{I}\right)}+W^{\left(\text{r}\right)}+W^{\left(\text{s}\right)}$ (14)

$W^{\left({\text{t}}_2\right)}=W^{\left(\text{f}\right)}$ (15)

${\tau }_{rz}^{\left({\text{t}}_1\right)}={\tau }_{rz}^{\left(\text{I}\right)}+{\tau }_{rz}^{\left(\text{r}\right)}+{\tau }_{rz}^{\left(\text{s}\right)}$ (16)

${\tau }_{\theta z}^{\left({\text{t}}_1\right)}={\tau }_{\theta z}^{\left(\text{I}\right)}+{\tau }_{\theta z}^{\left(\text{r}\right)}+{\tau }_{\theta z}^{\left(\text{s}\right)}$ (17)

${\tau }_{rz}^{\left({\text{t}}_2\right)}={\tau }_{rz}^{\left(\text{f}\right)}$ (18)

该问题的边界条件 [11] 为

$\{\begin{array}{l}{\Gamma }_H:{\tau }_{yz}^{{\text{t}}_1}\left(x,H\right)=0\\ {\Gamma }_R:{\tau }_{rz}^{{\text{t}}_1}\left(R,\theta \right)-{\tau }_{rz}^{{\text{t}}_2}\left(R,\theta \right)=-S\frac{\partial {\tau }_{\theta z}^{{\text{t}}_1}}{\partial \theta }\\ {\Gamma }_R:W^{\left({\text{t}}_1\right)}(R,\theta )=W^{\left({\text{t}}_2\right)}\left(R,\theta \right)\end{array}$ (19)

利用方程(19)可以推得 $A_n,B_n\left(n=0,n=\pm 1,n=\pm 2,\cdot \cdot \cdot \right)$ 满足如下形式的方程组

$\{\begin{array}{l}{\displaystyle \underset{n=-\infty }{\overset{\infty }{\sum }}{a}_{11}}{B}_n+a_{12}{A}_n=b_1\\ {\displaystyle \underset{n=-\infty }{\overset{\infty }{\sum }}{a}_{21}}{B}_n+a_{22}{A}_n=b_2\end{array}$ (20)

为了求解方程组，在方程组(20)的两边同乘 ${\text{e}}^{-im\theta }$ 并在 $\left[-\text{π},\text{π}\right]$ 上积分得到如下方程组

$\{\begin{array}{l}{\displaystyle \underset{n=-\infty }{\overset{\infty }{\sum }}{c}_{11}}{B}_n+c_{12}{A}_n=d_1\\ {\displaystyle \underset{n=-\infty }{\overset{\infty }{\sum }}{c}_{21}}{B}_n+c_{22}{A}_n=d_2\end{array}$ (21)

式中

$\begin{array}{l}{c}_{jk}=\frac{1}{2\text{π}}{\displaystyle {\int }_{-\text{π}}^{\text{π}}{a}_{jk}}{\text{e}}^{-im\theta }\text{d}\theta \\ d_j=\frac{1}{2\text{π}}{\displaystyle {\int }_{-\text{π}}^{\text{π}}{b}_j}{\text{e}}^{-im\theta }\text{d}\theta \end{array}$ $\left(j,k=1,2\right)$ (22)

对方程组截取有限项求解，可得到未知系数 $A_n,B_n\left(n=0,n=\pm 1,n=\pm 2,\cdot \cdot \cdot \right)$ 并代入(14)至(18)式可以得到介质内的总位移场 $W^{\left({\text{t}}_1\right)}$ ， $W^{\left({\text{t}}_2\right)}$ 和总应力场 ${\tau }_{rz}^{\left({\text{t}}_2\right)}$ ， ${\tau }_{\theta z}^{\left({\text{t}}_2\right)}$ 。

圆形夹杂边界处的动应力集中系数 $\gamma$ 描述了其应力集中的程度，定义为

$\gamma =\left|\frac{{\tau }_{\theta \text{z}}^{t_1}}{ku{W}_0^{\left(1\right)}}\right|$ (23)

其中 $ku{W}_0^{\left(1\right)}$ 代表入射波在自由场内产生的最大环向切应力的幅值。

3. 算例及分析

本文算例假设半空间介质中入射SH波的无量纲波数(波数k与圆形夹杂半径R的乘积) $kR=0.2,1,2$ (表示低、中、高频)入射平面波的入射角分别为：0， $\frac{\text{π}}{6}$ ， $\frac{\text{π}}{3}$ ， $H/R=150$ 以及表面参数 $S={10}^{-10},0.1,1$ 。

如图2所示，当 $S=0$ 时为宏观条件下半空间内圆形夹杂对SH波的散射，由图像可知该结论与现有的结论一致。当 $S=0$ ， ${\mu }_1=0$ 时为半空间内圆形孔洞对SH波的散射，该图像和 $S={10}^{-10}$ ， ${\mu }_1=0$ 时的图像

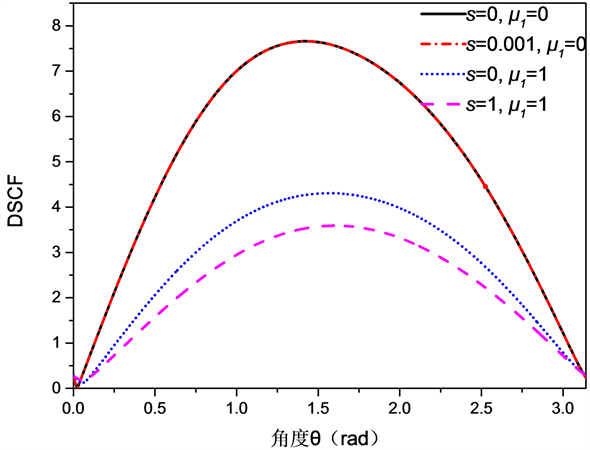
Figure 2. The ring direction angle distribution of the cyclic dynamic stress concentration coefficient at the boundary of the circular inclusion (hole) the level of incident wave kR = 2

图2. 当kR = 2时入射波水平入射时圆形夹杂(孔洞)边界处的环向动应力集中系数环向角分布

重合，该结论也与现有的结论相一致，从而验证了本文结论的准确性。

如图3所示，当 $S=1$ ， ${\mu }_1=1$ ， $H/R=150$ ， $kR=0.2,1,2$ 时，入射波水平入射时圆形夹杂边界处的环向动应力集中系数环向角分布。由图像可知无量纲波数越大，则SH波引起的圆形夹杂动应力集中越明显。当 $kR=2$ 时最大值为7.5。并且圆形夹杂边界处的应力集中系数的角度分布是对称的，这与实际情况是相吻合的。

如图4，当 $S=1$ ， ${\mu }_1=1$ ， $H/R=150$ ， $kR=0.2,1,2$ 时，入射波以 $\frac{\text{π}}{3}$ 入射时圆孔夹杂边界处的环向动

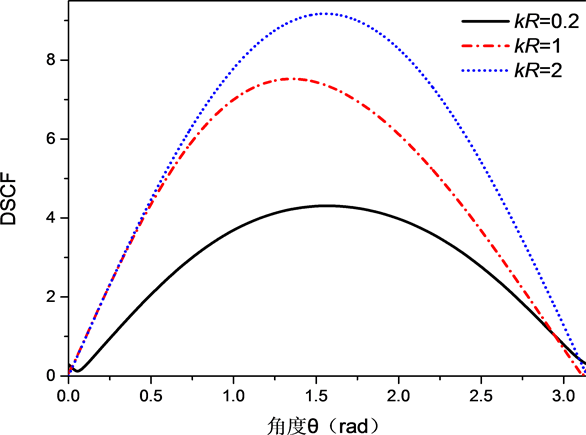
Figure 3. The ring direction angle distribution of the cyclic dynamic stress concentration coefficient at the boundary of the circular inclusion at the incident wave level

图3. 入射波水平入射时圆形夹杂边界处的环向动应力集中系数环向角分布

Figure 4. The ring direction angle distribution of the cyclic dynamic stress concentration coefficient at the incident wave at $\frac{\text{π}}{3}$ rad of incidence at the boundary of the circular inclusion

图4. 入射波 $\frac{\text{π}}{3}$ 入射时圆形夹杂边界处的环向动应力集中系数环向角分布

力应力集中系数环向角分布。从图像可知无量纲波数越大，则SH波引起的圆形夹杂动应力集中因子越大。这与水平入射时所得的结论一致，并且最大值是9。

如图5，当 $S=1$ ， ${\mu }_1=1$ ， $H/R=150$ ， $kR=0.2,1,2$ 时，入射波垂直入射时圆孔边界处的环向动应力集中系数环向角分布。由图可知当入射角垂直时动应力集中因子的变化趋势与以上两种情况相反是先减小后增大。其他与以上两种情况一致，动应力集中因子最大为10.2。

如图6，当 $kR=0.2$ ， $S={10}^{-10},0.1,1$ 时，入射波以水平入射时圆孔夹杂边界处的环向动力应力集中系

Figure 5. Circular angle distribution of the cyclic dynamic stress concentration coefficient at the boundary of a circular inclusion in a vertical incident wave incident

图5. 入射波垂直入射时圆形夹杂边界处的环向动应力集中系数环向角分布

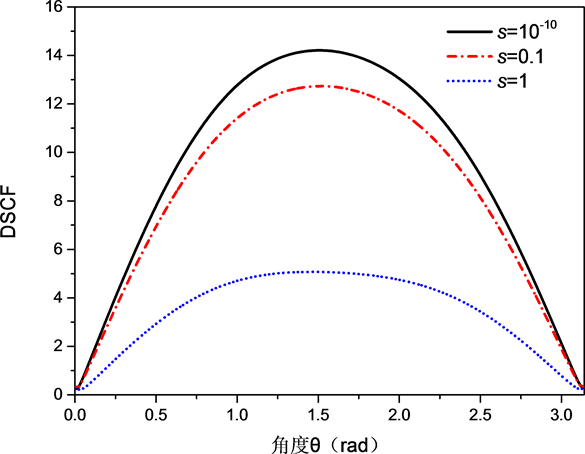
Figure 6. The ring direction angle distribution of the cyclic dynamic stress concentration coefficient at the boundary of the circular inclusion at the incident wave level when the incident wave is incident at kR = 0.2, S = 10⁻¹⁰, 0.1, 1

图6. 当kR = 0.2，S = 10⁻¹⁰，0.1，1时，入射波水平入射时圆形夹杂边界处的环向动应力集中系数环向角分布

数环向角分布情况。由图像可知当 $S={10}^{-10}$ ，也就是S趋近于零时动应力集中因子最大为14，当 $S=1$ 时，动应力集中因子为4.2，从而可得表面参数S越小，SH波引起的圆孔夹杂处的动应力集中因子越强。

如图7，当 $kR=2$ ， $S={10}^{-10},0.1,1$ 时，入射波以水平入射时圆孔夹杂边界处的环向动力应力集中系数环向角分布情况。由图像可知在高频下与在低频下结论是一致的，由此可得不论是在微观还是在宏观条件下当表面参数S越大，SH波引起的圆孔夹杂处的动应力集中因子越小。

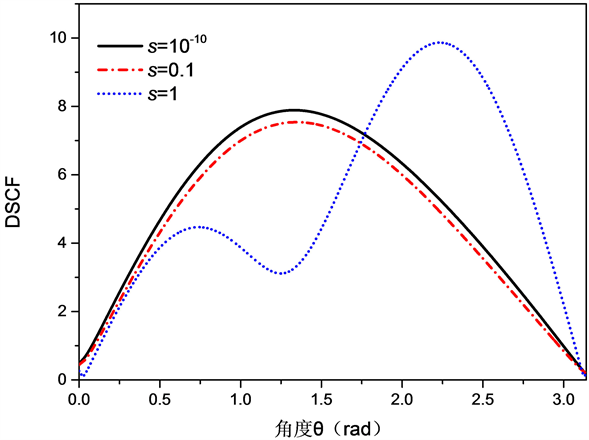
Figure 7. The ring direction angle distribution of the cyclic dynamic stress concentration coefficient at the incident wave level when the incident wave is incident at the level of kR = 0.2, S = 10⁻¹⁰, 0.1, 1

图7. 当kR = 0.2，S = 10⁻¹⁰，0.1，1时，入射波水平入射时圆形夹杂边界处的环向动应力集中系数环向角分布

Figure 8. When the incident wave is $kR=0.2$ , $S={10}^{-10},0.1,1$ the ring direction of the dynamic stress concentration coefficient is distributed at the boundary of the circular inclusion at the $\frac{\text{π}}{3}$ rad incident

图8. 当kR = 0.2，S = 10⁻¹⁰，0.1，1时，入射波 $\frac{\text{π}}{3}$ 入射时圆形夹杂边界处的环向动应力集中系数环向分布

如图8，当 $kR=0.2$ ， $S={10}^{-10},0.1,1$ 入射波以 $\frac{\text{π}}{3}$ 入射时圆孔夹杂边界处的环向动力应力集中系数环向角分布，与图6，图7得出的结论一致。

4. 结论

本文利用复变函数法、多极坐标法、虚源法和Graf加法公式研究了在纳米尺度下半空间内浅埋圆形夹杂对稳态入射SH波的散射问题，并给出不同介质的位移场，应力场。通过数值算例分析得到：

1) 在纳米尺度下圆形夹杂边界处的应力集中程度显著，表面参数 $S$ 越小，引起的圆形夹杂边界处的应力集中程度越强。

2) 在纳米尺度下，无量纲波数 $kR$ 越大，引起的圆形夹杂边界处的应力集中程度越强，和宏观条件下一致。

基金项目

国家自然科学基金(1106004和11362009)。