变质量运动火箭运动方程的推导

Derivation of Motion Equation of Variable Mass Moving Rocket

摘要: 本文以对动量守恒定律的表述：一个系统不受外力或所受外力之和为零或内力远远大于外力，这个系统总动量的增量为零作为基础，并根据动量定理，运用比较简洁的方式，得出了变质量运动火箭运动方程。文中推导过程将更易于读者对变质量运动方程的理解。

Abstract: In this paper, the law of conservation of momentum is expressed: a system is free from external force or external force as zero or internal force is far greater than external force. The increment of the total momentum of the system is zero as the basis, and the equation of motion of fire and arrow with variable mass motion is obtained in a relatively concise way according to the momentum theorem. The derivation process in this paper will make it easier for readers to understand the equation of motion of variable mass.

1. 引言

如果一个系统不受外力或所受外力的矢量和为零的时候，我们通常运用动量守恒定律研究系统的运动规律。比如：碰撞问题、反冲问题、变质量运动等等。动量守恒定律是自然界中最重要最普遍的守恒定律之一，它既适用于宏观物体，也适用于微观粒子；既适用于低速运动物体，也适用于高速运动物体；它既适用于保守系统，也适用于非保守系统。《普通物理学》的教材当中，都有涉及在忽略重力、空气阻力的情况下，运用动量守恒定律推导变质量运动的火箭运动方程的推导。但是，在当前各个版本的教材当中，对动量守恒定律的运用并不尽相同，虽然结果一样，但推导的过程却存在着差别。比如：《普通物理学》(北京大学物理系普通物理教研室编)、《普通物理学》第三版(程守洙、江之永主编)等书分别使用 [1] [2] [3]

$mv=\left(m+\text{d}m\right)\left(v+\text{d}v\right)+\left(-\text{d}m\right)\left(v-u\right)$ (1)

的方式，而物理学力学(复旦大学、上海师范大学编)当中使用

$mv=\left(m+\text{d}m\right)\left(v+\text{d}v\right)+\left(-\text{d}m\right)\left(v+\text{d}v-u\right)$ (2)

的方式。

这样的表述常易于会给学生带来理解上混乱。一些文章也对相关问题作了进一步的探讨 [4] 。本文将从另外的角度出发，通过动量守恒定律简洁推导出变质量运动的火箭运动方程。

2. 变质量运动火箭运动方程的推导

动量守恒定律的一般描述为：当一个系统不受外力或者系统所受的外力之和为零的时候，系统将保持总动量不变，该结论就叫做动量守恒定律。所谓系统的总动量保持不变，也即系统总动量的增量为零。这两种表述的等价的。也就是说，我们可以将动量守恒定律表示为：当一个系统不受外力或者系统所受的外力之和为零的时候，这个系统总动量的增量为零 $\left(\Delta P=0\right)$ 。

以此观点为基础，我们按照一般教材中的假设 [5] [6] [7] ：以燃料和箭体所组成的系统作为研究的系统，选取地球为参考系，正方向为火箭前进的方向。假设在t时刻，火箭的质量为m，速度为v，t到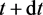时间内，质量为dm的燃料燃烧，并以速度C相对于箭体向后喷出，在此过程中，火箭质量减为 $m-\text{d}m$ ，速度增为dv，与喷气的速度C方向相反。

根据动量定理：作用在物体上合外力的冲量等于物体动量的增量，即： $F\text{d}t=\text{d}P$ 。在此过程中，火箭和燃料动量的增量分别为： $\left(m-\text{d}m\right)\text{d}v$ 和 $C\text{d}m$ 。因为系统总动量的增量为零 $\left(\Delta P=0\right)$ ,所以，我们可以得到火箭运动微分方程为：

$\left(m-\text{d}m\right)\text{d}v+C\text{d}m=0$ (3)

(3)式展开后可得：

$m\text{d}v-\text{d}m\text{d}v+C\text{d}m=0$ (4)

略去高价无限小，得：

$m\text{d}v+C\text{d}m=0$ (5)

假设火箭的初始时刻 $\left(t=0\right)$ 时，质量为 $M_0$ ，速度为0，经过一段时间t之后，速度为v，质量为M。那么，对(5)式进行分离变量后，可得：

$-\frac{\text{d}v}{C}=\frac{\text{d}m}{m}$ (6)

两边求定积分：

(7)

最后得到：

$v=C\ln \frac{M_0}{M}$ (8)

和齐奥尔科夫斯基火箭方程式一致。

3. 结论

本文当中，我们从对动量守恒定律表述：一个系统不受外力或所受外力之和为零或内力远远大于外力，这个系统总动量的增量为零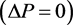出发，通过简洁推导，得出了变质量运动火箭运动方程，并通过进一步的推导，得出了和齐奥尔科夫斯基火箭方程式一致的结果。推导过程更易于理解。本文虽然是以火箭运动方程为例进行的推导，但得到的结果对其它变质量运动，如：雨滴降落过程中，不断出现雨滴的冲并过程，导致的雨滴质量增加；细绳自然降落时研究对象的改变导致的质量变大等 [8] 变质量问题都具有普遍意义。