用于直下式激光背光模组的衍射光学元件设计

Diffractive Optical Element for Direct-Lit Laser Backlight Unit

摘要: 激光光源用于直下式背光时，需要将小尺寸的椭圆形光斑整形为符合显示面积要求的矩形均匀光斑。针对激光发散角小、用于直下式背光整形距离过长的问题，利用衍射光学元件算法，设计了一款对激光二极管(Laser diode, LD)进行整形的衍射光学元件(diffractive optical element, DOE)。首先，确定输入和输出光场的振幅分布，以及成像距离。接着，利用MATLAB根据衍射公式和盖师贝格–撒克斯通算法计算出DOE的相位分布。然后，将得到的DOE相位数据带入仿真软件VirtualLab中进行仿真。仿真结果发现光斑存在较严重的畸变，并且能量利用率不高。对输出光场分布进行了改进，重新设计了DOE，并进行了仿真。结果表明：优化后的DOE能有效地将LD出射的椭圆形光斑整形为14 mm × 11 mm的矩形光斑，能量利用率从之前的46.69%上升到56.08%，均匀性为从80.59%提升到87.16%。采用本文设计的DOE能实现激光光束从椭圆形高斯型光斑到矩形均匀光斑的整形要求，满足直下式背光亮度和均匀性的要求。

Abstract: When used in a direct-lit backlight, the ellipse light spot of a laser diode has to be modulated to be rectangular. Aiming at the problem of small divergence angle and long mixing distance, a diffractive optical element for shaping laser light spot is designed by using diffractive optical element algorithm. First, the amplitude distribution of the input and output light fields and the imaging distance are determined. The diffraction formula and Gerchberg-Saxton algorithm are applied to calculate the phase distribution of the DOE in Matlab. Then the obtained phase distribution is input into the simulation software Virtual Lab for simulation. The simulation results show there exists the worse distortion on the spot and the power efficiency is not very high. The output light field distribution is modified and the DOE is then redesigned. The results show that the optimized DOE can effectively shape the elliptical light spot emitted by the LD into a rectangular spot of 14 mm × 11 mm. The energy efficiency is improved to 56.08% from the original 46.69%. The uniformity is improved to 87.16% from 80.59%. The design of the DOE in this paper can realize the shaping requirements of laser beam from circular Gauss beam to rectangular uniform spot, satisfying the requirements of a direct-lit backlight unit on luminance and uniformity.

1. 引言

激光具有良好的单色性，光谱范围很小。随着激光二极管(Laser diode, LD)的发展，激光器的体积越来越小型化，激光光源也逐渐被用在各种投影显示系统中，例如：激光电视 [1] [2] [3] 和激光投影机 [4] 。虽然激光光源在投影和激光电视中获得广泛应用，但是作为液晶平板显示的背光源时，激光光源还存在一些问题，如：激光光斑尺寸一般较小，无法完整照明整个液晶面板；激光光斑的能量分布呈典型的高斯分布，需要进行均匀化。针对激光光源用于液晶显示背光模组存在的问题，国内外的多家机构和学者开展了研究。2012年，日本Yuuto Okuda等研究人员研制了采用侧出LD配合平面布置光纤结构的激光背光模组 [5] 。2013年，山东大学孙玉宝提到了两种侧入式激光背光模组的结构 [6] 。2016年，北京工业大学的王志平等人提出了一种基于导光模块的激光背光光源设计 [7] ，长光所的赵致童等人对侧出发光光纤上出光孔的深度进行研究实现出光孔的均匀出光 [8] 。可以看出现有的激光背光模组中，设计的光源多是面向侧出式背光模组，侧出式背光需要结合导光板使用。侧出LD配合平面布置光纤结构的背光仍然需要较大的混光距离。如果不采用平面光纤结构，直接采用现有的扩散膜的混光方法，则将导致背光模组过长，无法满足实际应用要求。

衍射光学元件(Diffractive Optical Element，DOE)在激光整形领域有着广泛的应用 [9] [10] [11] [12] 。本文就是试图利用衍射光学理论设计衍射光学元件，以便对激光光束进行整形均光，以适用于直下式背光模组。通过DOE元件进行整形均光，可以减小背光模组的体积，降低背光模组的重量。

2. 直下式激光背光模组结构

2.1. 现有直下式LED背光模组结构

现有的用于头盔显示的0.63英寸的直下式背光模组是由2 × 2阵列发光二极管(Light Emitting diode, LED)和两片扩散膜组成，如图1所示。

图中包括四个LED发光光源，经过两层扩散膜后会得到亮度均匀的矩形光斑。

2.2. 直下式LD背光模组结构

将LED换成LD后，背光模组的结构也会有相应的变化，如图2所示。

图中位于背光模组中间的是LD，第二个元件表示用于激光整形的DOE。对于0.63英寸、长宽比为4:3的液晶显示区域，背光显示面积要略大于显示面积，设定为14 mm × 11 mm。背光整体厚度限制在15 mm之内。故设定LD出射的光斑通过DOE后在距离DOE10 mm的平面上形成尺寸为14 mm × 11 mm的均匀矩形光斑。

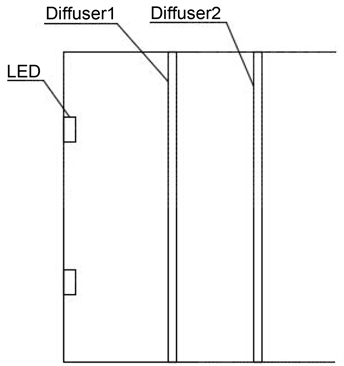
Figure 1. Direct-lit LED backlight unit

图1. 直下式LED背光模组

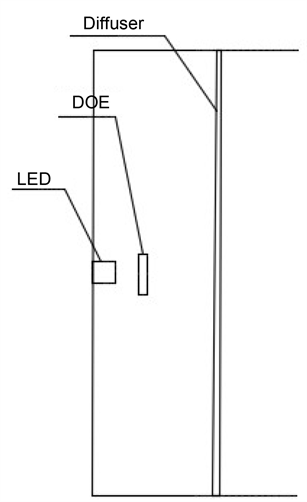
Figure 2. Direct-lit laser backlight unit

图2. 直下式激光背光模组

3. 衍射光学元件设计理论

3.1. 理论基础

当入射光场垂直入射DOE所在平面，假定入射光场的复振幅为 $g_0\left(x_1,y_1\right)$ ，DOE的复振幅透过率为 $t\left(x_1,y_1\right)$ ，则通过DOE后形成光场分布的复振幅分布可以表示为 [13] ：

$g\left(x_1,y_1\right)=g_0\left(x_1,y_1\right)\ast t\left(x_1,y_1\right)$ (1)

衍射成像面上的光场分布(即输出平面的光场分布)通过基尔霍夫衍射公式求得为 [13] ：

$u\left(x_2,y_2\right)=\frac{1}{i\lambda }{\displaystyle \int {\displaystyle {\int }_{-\infty }^{\infty }g\left(x_1,y_1\right)\frac{\exp \left(ikr\right)}{r}K\left(\theta \right)\text{d}{x}_1\text{d}{y}_1}}$ (2)

式中：r表示光的传播距离，可表示为：

$r=\sqrt{{\left(x_2-x_1\right)}^2+{\left(y_2-y_1\right)}^2+z^2}$ (3)

其中，z是输入平面和输出平面之间的距离。倾斜因子 $K\left(\theta \right)$ 表示为 [13] ：

$K\left(\theta \right)=\frac{r+z}{2r}$ (4)

这样，根据已知的入射光场分布及需要的输出光场分布，就可以推导出DOE的复振幅透过率，进而得到DOE的表面形貌。

3.2. DOE理论设计

由于输入光场的复振幅分布和输出光场的复振幅分布为已知条件，求解DOE的复振幅分布就是求解公式(2)所形成的非线性方程。

盖师贝格—撒克斯通算法(GS算法)是1971年Gerchberg和Saxton首先提出的 [13] ，用于解决相位恢复问题。GS算法的基本思路是已知初始相位和事先给定的入射光场分布，通过做正向衍射变换，得到输出平面光场分布；在输出平面引入限制条件，以期望的光场振幅分布取代原光场振幅分布，同时保持相位不变；然后做逆向衍射变换，得到输入平面光场分布；在输入平面引入限制条件，以给定的光场振幅分布取代原光场分布，并保持相位不变；接着重复上述正向和逆向衍射变换，直到得到满意的结果或者达到足够的循环次数。算法流程图如图3所示。

从LD出射的光束能量呈高斯型分布，其振幅分布可用数学公式表示为 [13] ：

$U_{in}\left(x_1,y_1\right)=\exp \left[-\left(x_1^2+y_1^2\right)/{\omega }^2\right]$ (5)

Figure 3. GS algorithm flow chart

图3. GS算法流程图

式中 $\omega$ 表示光束的束腰半径。

理想的输出光场的归一化数学表达式为 [13] ：

$U_{\text{ideal}}\left(x_2,y_2\right)=\{\begin{array}{l}1x_2,y_2\in S\\ 0x_2,y_2\notin S\end{array}$ (6)

式中S表示理想输出光场的范围。

衍射光学元件DOE的相位分布可以通过最终得到的相位分布减去初始相位分布求得，表示为 ${\varphi }_n\left(x_1,y_1\right)-{\varphi }_0\left(x_1,y_1\right)$ 。

在实际情况下，光波相位的改变是通过引入光程差。光程差是光波在均匀介质中传播时通过不同距离产生的。所以得到了DOE的相位分布后在实际中进行制作时需要将相位转化为微结构的高度。

4. 软件仿真及优化

根据上一节的理论依据和算法流程在MATLAB中对GS算法进行编程。将输入光场和输出光场的复振幅分布带入程序，计算出DOE的相位分布 ${\varphi }_{doe}\left(x,y\right)$ 。然后通过相位与微结构高度之间的关系计算出设计的表面微结构的高度分布 $h_{doe}\left(x,y\right)$ 。然后将得到的相位数据导入仿真软件中进行仿真验证。

在实际的背光模型中，由于DOE只能放置在LD外部(不能放置在束腰处)，DOE与LD之间存在一定的距离。LD出射的光束在水平偏振方向和垂直偏振方向的发散角度不同，导致出射光斑为椭圆形光斑，其振幅分布呈高斯型。因此在设计时要根据DOE所在位置的光斑大小进行计算。输入光斑的尺寸可以通过发散角和出射距离进行计算：

$R_0=r_0+d\ast \tan \theta$ (7)

式中： $R_0$ 表示DOE所在平面的光斑半径； $r_0$ 表示原始光斑半径；d表示DOE所在平面与出光孔径所在平面之间的距离；θ表示发散角度。

根据平行偏振方向和垂直偏振方向上的发散角可以得到入射在DOE上的光斑尺寸。输入光场的分布可以表示为：

$U_{in}\left(x,y\right)=\exp \left[-\left(\frac{x_1^2}{R_x^2}+\frac{y_1^2}{R_y^2}\right)\right]$ (8)

在设计过程中，为了提高计算速度而采用基于傅里叶变换形式的菲涅尔衍射公式进行衍射计算。理想输出光场分布设置为14 mm × 11 mm的矩形带入设计程序中进行计算，得到对应的DOE的相位分布。在VirtualLab7.0.2仿真软件中建立相应的光学传播系统，并将计算出的DOE相位导入进行仿真，得到面上的光场分布，如图4所示。

从结果中可以看到，仿真得到的光斑尺寸要大于理想光斑尺寸(黑色虚线框)，并且在光斑的上下两边存在严重的畸变。经测量，理想光斑尺寸内的能量为37.35 mW。根据公式(9)可以计算能量利用率，光源总能量为80 mW，能量利用率为46.69%。过大的光斑会降低目标范围内DOE的能量利用率，进而降低背光亮度。

$\eta =\frac{E_{\text{target}}}{E}$ (9)

式中η表示能量利用率； $E_{\text{target}}$ 表示目标范围内的能量；E表示光源总能量。

根据《数字电视平板显示器测量方法》标准定义的九点法对目标范围内的光斑均匀性进行了计算 [14] 。九点布置图如图5所示，九点照度数据如表1所示。

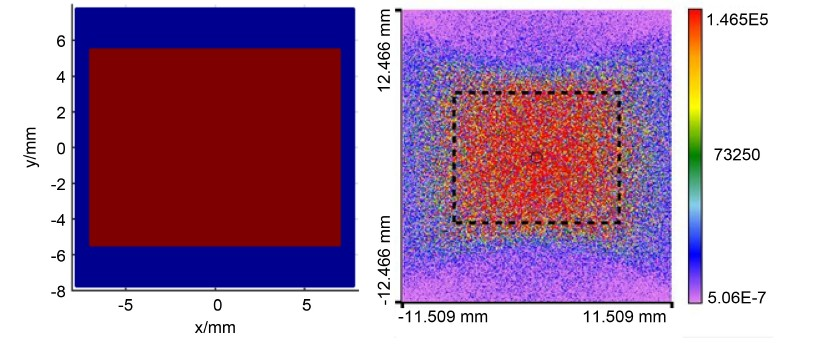
Figure 4. Ideal light field distribution and its simulation results

图4. 理想光场分布及相应的仿真结果

Figure 5. 9 points

图5. 9点布置图

Table 1. Illumination value of nine points

表1. 九点照度值

均匀性的计算根据公式(10)

$u=I_{\min }/I_{\text{ave}}$ (10)

式中u表示均匀性； $I_{\min }$ 表示最小照度值； $I_{\text{ave}}$ 表示平均照度值。

经计算得到平均照度为113,241.93lx，均匀性为80.57%。

经过分析，图4(b)中的畸变是因为在设计过程中使用的衍射计算公式是基于菲涅尔衍射的。菲涅尔衍射公式对基尔霍夫衍射公式中波的传播距离r的计算进行了近似。通过牛顿二项式对r进行分解可以得到公式(11)：

$r=z+\frac{{\left(x_2-x_1\right)}^2+{\left(y_2-y_1\right)}^2}{2z}+o\left(\frac{{\left({\left(x_2-x_1\right)}^2+{\left(y_2-y_1\right)}^2\right)}^2}{8z^3}\right)$ (11)

当z远大于x₁、y₁、x₂、y₂时，最后一项在exp(ikr)中影响很小，可以忽略。但是在文中的设计要求下，z与x₂、y₂相差不大，导致最后一项在计算过程中不应该被忽略。而菲涅尔衍射公式忽略了这项，就会在光波的传播距离的计算上带来一个误差，从而影响光波的传播到目标平面的相位。这个误差会影响目标平面上的各点的振幅大小。

通过对理想输出光场的形状和振幅分布进行一定的变换可以使实际衍射场更接近理想光场 [15] 。对基尔霍夫的相位项进行更精确的近似。令 $R=\sqrt{x_2^2+y_2^2+z^2}$ ，对r进行展开：

$r=R+\frac{-2x_1{x}_2-2y_1{y}_2+x_1^2+y_1^2}{2R}+o\left(\frac{{\left(-2x_1{x}_2-2y_1{y}_2+x_1^2+y_1^2\right)}^2}{8R^3}\right)$ (12)

忽略式(12)中第三项带来的相位影响，得到近似的衍射公式为：

$\begin{array}{c}u\left(x_2,y_2\right)=\frac{\exp \left(ikR\right)}{i\lambda z}\frac{z}{R}{\displaystyle \int {\displaystyle {\int }_{-\infty }^{\infty }g\left(x_1,y_1\right)\exp \left(ik\frac{x_1^2+y_1^2}{R}\right)}}\\ \times \exp \left[-\frac{ik}{z}\left(x_1\frac{z{x}_2}{R}+y_1\frac{z{x}_2}{R}\right)\right]\text{d}{x}_1\text{d}{y}_1\end{array}$ (13)

$\{\begin{array}{l}{x}_3=\frac{z}{R}{x}_2\\ y_3=\frac{z}{R}{y}_2\\ u\left(x_2,y_2\right)=\frac{z}{R}u\left(x_3,y_3\right)\end{array}$ (14)

按式(13)对理想输出光场进行坐标变换可以使实际的输出光场更接近于矩形的输出光场。

将输入光场分布和修正后的输出光场分布带入设计程序中重新进行计算，可以得到对应的DOE相位分布。在VirtualLab中建立相应的光学传播系统，并将计算出的DOE相位导入进行仿真。在10 mm上得到相应的衍射图样。修改后的理想输出光场和仿真得到的输出光场如图6所示。

从仿真结果的照度图中可以看出光场主要集中在目标范围14 mm × 11 mm内，衍射场的尺寸略大于理想的尺寸。和修改前的DOE的衍射场比较，在上下两边基本没有畸变。经测量，理想光斑尺寸内的能量为44.86 mW，能量利用率为56.08%。按照九点法对目标范围内的光斑均匀性进行测量。九点的照度数据如表2。

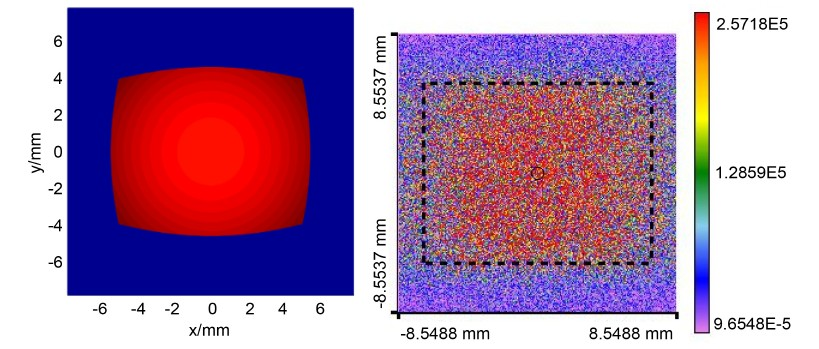
Figure 6. The optimized ideal light field distribution and its simulation results

图6. 改进后的理想输出光场及相应的仿真结果

Table 2. Illumination value of nine points of the optimized design

表2. 改进设计后的九点照度值

经计算得到平均照度为150,284.65lx，均匀性为87.16%。能量利用率和均匀性都得到提升。

5. 结论

本文针对0.63英寸直下式激光背光模组需要在较小的距离进行整形的要求，设计了基于衍射理论的光学元件，并进行了仿真验证。仿真结果表明：设计的DOE能有效地将LD出射的椭圆形光斑整形为14 mm × 11 mm的矩形光斑，能量利用率达到56.08%，平均照度为150,284.65lx，均匀性为87.16%，满足背光实际使用要求。

基金项目

安徽省科技重大专项项目(No. 17030901003, No. 17030901033, No. 16030901001)。

NOTES

^*通讯作者。