大规模MIMO系统中的信号子空间变步长LMS自适应波束形成算法

Signal Sub-Space Based Variable Step Size LMS Adaptive Beamforming Algorithm for Massive MIMO Systems

摘要: 本文针对变步长LMS自适应波束形成算法在相关矩阵特征值分散时收敛特性不理想的问题，提出一种可用于大规模MIMO系统的信号子空间变步长LMS自适应波束形成算法(SS-VSLMS)。该算法中的权矢量仅保留信号子空间分量，可获取基于指数因子最优步长，提高算法收敛速度；同时引入误差相关性分析，最大限度减小稳态误差；并通过提取信号子空间的权矢量，提高系统抗干扰能力。仿真实验表明，该改进算法能够满足大规模MIMO系统的收敛性和抗干扰要求。

Abstract: In this paper, an improved variable step size LMS adaptive beamforming algorithm based on signal sub-space (SS-VSLMS) is proposed to solve some problems of LMS adaptive beamforming algorithm when the eigenvalue of the correlation matrix is not ideal for large scale MIMO systems. The weight vector in the algorithm only preserves the subspace component of the signal, and can obtain the optimal step length based on the exponential factor and improve the convergence speed of the algorithm. At the same time, the error correlation analysis is introduced to minimize the steady state error, and the power vector of the signal subspace is extracted to improve the an-ti-interference ability of the system. Simulation results show that the improved algorithm can meet the convergence and anti-interference requirements of large-scale MIMO systems.

1. 引言

在大规模MIMO系统中，不增加阵列天线带宽的前提下，提升每一个窄带平坦子信道上获得更大的信道容量，是成倍地提高通信系统容量和频谱效率的有效手段 [1] 。采用阵列天线的MIMO系统具有极高的系统容量、更好的系统服务质量 [2] [3] 。对于存在几十、甚至上百个天线阵元的大规模MIMO无线移动通信系统而言，自适应波束形成是最关键的基础技术 [4] [5] [6] ，它可通过调节基站接收阵元的加权幅度和加权相位，来改变收发阵列之间的方向图，使阵列天线的主瓣对准期望用户，同时阵列天线方向图的零点和副瓣对准其他用户 [7] ，以提高接收信噪比。

自适应波束形成算法中，LMS算法具有步骤简单、计算量较小、易于硬件实现等优点 [8] ；但是，LMS算法用于大规模MIMO系统时，具有收敛特性对步长和初始值敏感的不足，其收敛速度受数据相关矩阵特征值分布的影响较大，尤其是特征值较分散时，收敛速度极慢，不利于硬件实现和实时应用 [9] 。针对自适应LMS算法存在的这些问题，本文提出了一种用于大规模MIMO系统的信号子空间变步长LMS (SS-VSLMS)自适应波束形成算法。其基本思想是：1) 对LMS算法的S函数模型进行改进，提出了一种非线性对数函数模型，通过调节指数因子以及其他参数，优化步长，得到最优的收敛性；2) 对LMS算法的权矢量进行改进，抛弃噪声子空间分量，仅保留信号子空间分量，提高算法的抗干扰能力；3) 对变步长LMS (VSLMS)算法进行改进，引入误差相关矩阵，可进一步减小稳态误差，加快旁瓣的衰减速度，进一步提高波束保形能力。

2. 系统简化模型

通过对输入信号进行分帧分组，编码映射，可以得到频域发送信号，再经过IFFT，并串变换，DA变换可以得到一个完整的OFDM信号 [10] 。接收机对接收到的这些信号进行下变频，AD变换，然后在时域做波束形成，再进行FFT变换，得到频域形式的接收信号，整个OFDM系统框图如图1所示。

发送信号

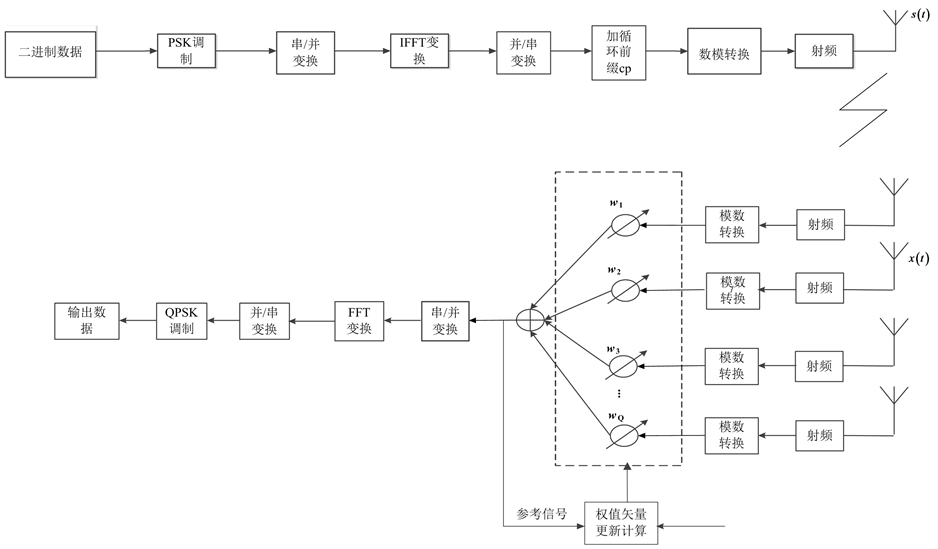
Figure 1. Simplified model block diagram of a massive MIMO system (single output multiple receive, OFDM modulation and demodulation)

图1. 大规模MIMO系统简化模型框图(单发多收，OFDM调制解调)

一体化系统发送的OFDM等效复基带帧信号为

$s\left(t\right)=\underset{u=1}{\overset{Ns}{{\displaystyle \sum }}}\underset{n=1}{\overset{Nc}{{\displaystyle \sum }}}Tx\left(u,n\right)\exp \left(j2\text{π}\left(n-1\right)\Delta ft\right)$ (1)

式中，Ns为一帧OFDM信号含有的符号个数，u为符号索引；Nc为每一个OFDM符号含有的子载波个数，n为子载波索引； $Tx\left(u,n\right)$ 为第u个符号上第n个子载波上的调制数据， $\Delta f$ 为相邻子载波间隔，由复信号正交性条件，有： $$ 。

由于OFDM帧信号中的符号个数不影响算法结果，为了简便起见，可以假设一帧数据仅包含一个OFDM符号，即：

$s\left(t\right)=\underset{n=1}{\overset{Nc}{{\displaystyle \sum }}}Tx\left(n\right)\exp \left(j2\text{π}\left(n-1\right)\Delta ft\right)$ (2)

接收信号

在阵列信号处理中，当信源与观测阵列之间存在视距传播、直射波信号强度足够大时，信源能量集中在离散的角度，点信源模型能够有效地逼近信号的实际传播环境。在雷达和无线通信环境中，由于作用距离较远，一般采用远场模型。

一体化系统的接收端采用均匀直线阵(ULA, Uniform Linear Array)接收信号，阵列天线模型如图2所示。天线阵列的阵元数为N，阵元间距为d。假设道路中有L个信号，相对于系统的时延为 ${\tau }_l$ ，信号l的DOA [11] [12] [13] 分别为 ${\theta }_l$ ， ${\theta }_l$ 表示信号l与阵列法线之间的夹角。

经推导可以得到接收端的等效复基带信号表达式：

$x\left(t\right)=\left[x_1\left(t\right)x_2\left(t\right)\cdots x_N\left(t\right)\right]$ (3)

其中， $a\left({\theta }_l\right)$ 为阵列的导向矢量，

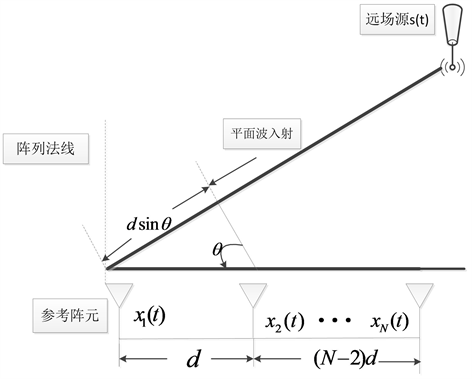
Figure 2. Structure model of uniform linear array (ULA) antenna

图2. 均匀线阵(ULA)天线结构模型

$a\left({\theta }_l\right)=\left[1\exp \left(j2\text{π}\frac{d}{\lambda }\sin {\theta }_l\right)\cdots \exp \left(j2\text{π}\frac{d}{\lambda }\left(N-1\right)\sin {\theta }_l\right)\right]$ (4) $x_m\left(t\right)=\underset{l=1}{\overset{L}{{\displaystyle \sum }}}{b}_l\exp \left(j2\text{π}\frac{d}{\lambda }\left(m-1\right)\sin {\theta }_l\right)\underset{n=1}{\overset{Nc}{{\displaystyle \sum }}}Tx\left(m,n\right)\exp \left(j2\text{π}\left(n-1\right)\Delta f\left(t-{\tau }_l\right)\right)+w\left(t\right)$ (5)

式中， $b_l$ 为幅度衰减， ${\tau }_l$ 为时延， $w\left(t\right)$ 为高斯白噪声，对于每一根接收天线， $$ ，式(5)可以表示为：

$x_m\left(t\right)=\underset{l=1}{\overset{L}{{\displaystyle \sum }}}{b}_l\exp \left(j2\text{π}\frac{d}{\lambda }\left(m-1\right)\sin {\theta }_l\right)\underset{n=1}{\overset{Nc}{{\displaystyle \sum }}}Tx\left(n\right)\exp \left(j2\text{π}\left(n-1\right)\Delta f\left(t-{\tau }_l\right)\right)+w\left(t\right)$ (6)

3. LMS自适应波束形成算法原理

最小均方算法是Widrow B等人于20世纪60年代提出的 [14] 。由于该算法具有实现简单以及对信号统计特性变化具有稳定性的特点而获得广泛应用。LMS算法是基于MMSE准则和梯度估计的最陡下降原理导出的。该算法适用于环境中信号的统计特性平稳但未知的情况，基于此算法的各种形式的阵列天线已广泛应用于自适应天线系统，并在抗多径干扰方面取得了良好的效果。LMS算法原理框图如图3所示。

LMS算法的理论基础是最陡下降法，这也是许多自适应算法的基础。最陡下降法是一种无需做矩阵求逆的解正规方差的方法。由MMSE准则可知该准则下的最优权向量为式(7)，为了不直接对 $R_{xx}$ 求逆求解 $w_{opt}$ ，首先设置一个 $w$ 的初值 $w\left(0\right)$ ，令 $\zeta =E\left\{{\left|e\left(n\right)\right|}^2\right\}$ ，沿着 $\zeta$ 减少的方向调整 $w$ 可以找到 $w_{opt}$ 。由于 $\zeta$ 增长最快的方向即梯度方向，那么 $\zeta$ 减少最快的方向即负梯度方向。因此，可以采用递推公式调整 $w$ 以寻求 $w_{opt}$ ：

$w\left(n+1\right)=w\left(n\right)-\mu \left(2R_{xx}w\left(n\right)-2r_{xd}\right)$ (7)

式中 $\mu$ 为迭代步长，控制着算法的收敛速度。

采用最陡下降法需要知道性能函数梯度的精确值 ${\nabla }_w\zeta =2R_{xx}w\left(n\right)-2r_{xd}$ ，这就意味着输入信号 $x\left(n\right)$ 和期望信号 $d\left(n\right)$ 平稳且其二阶统计特性已知，这样根据 $x\left(n\right)$ 和 $d\left(n\right)$ 的采样值可以估计 $R_{xx}$ 和 $r_{xd}$ 。

LMS算法用梯度估计值 ${\hat{\nabla }}_w\zeta$ 代替梯度 ${\nabla }_w\zeta$ ，用瞬时平方误差性能函数 ${\left|e\left(n\right)\right|}^2$ 代替均方误差性能函数 $E\left[{\left|e\left(n\right)\right|}^2\right]$ ，有：

$w\left(n+1\right)=w\left(n\right)-\mu {\hat{\nabla }}_w\zeta =w\left(n\right)-\mu {\nabla }_w{\left|e\left(n\right)\right|}^2$ (8)

又

$e\left(n\right)=d\left(n\right)-w^{H}x\left(n\right)$ (9)

所以

${\nabla }_w{\left|e\left(n\right)\right|}^2=-2e^{*}\left(n\right)x\left(n\right)$ (10)

因此，LMS算法的递推公式为：

$w\left(n+1\right)=w\left(n\right)+2\mu e^{*}\left(n\right)x\left(n\right)$ (11)

式中，在取值满足 $0<\mu <\frac{1}{{\lambda }_{\max }}$ 时才能保证算法收敛， ${\lambda }_{\max }$ 是自相关矩阵 $R_{xx}$ 的最大特征值。表1说明了LMS的算法步骤。

Figure 3. LMS algorithm

图3. LMS算法

Table 1. LMS algorithm

表1. LMS算法

4. 一种新的变步长自适应LMS (SS-VSLMS)算法

变步长LMS算法(VSLMS)的思想是，在初始收敛阶段或未知系统参数发生变化时，步长应比较大，以便有较快的收敛速度和对时变系统的跟踪速度，而在算法收敛后，不管主输入干扰有多大，都应保持很小的调整步长以达到很小的稳态误调噪声 [15] [16] 。为了进一步提高算法的抗干扰能力，可以引入误差相关值，这样可以抑制不相关噪声引起的稳态误差。基于以上考虑，提出一种新的基于非线性对数函数模型的VSSLMS函数，其表达式如下：

$\mu \left(n\right)=\beta \left(1-\frac{1}{\log \left(1+\exp \left(\alpha \left|e\left(n\right)e\left(n-1\right)\right|\right)\right)}\right)$ (12)

式中， $\alpha$ 是控制函数形状的常数， $\beta$ 是控制函数范围的常数。论文仿真中， $\alpha =3$ ， $\beta =0.05$ 。

由于噪声的存在，对波束形成有一定的影响，并使得自适应方向图发生畸变。因此，需要抛弃权矢量中的噪声子空间中分量，而仅保留其在信号子空间中的分量，这样，可以达到进一步提高系统抗干扰能力的目的。具体步骤为：

第一步，对接收信号的协方差矩阵进行特征分解：

$R=\left[U_A,U_O\right]\left[\begin{array}{cc}{\sum }_A+{\sigma }^{2}I& 0\\ 0& {\sigma }^{2}I\end{array}\right]\left[\begin{array}{c}{U}_A^H\\ U_O^H\end{array}\right]=U_A{\sum }_A{U}_A^H+{\sigma }^{2}I$ (13)

式中， $U_A$ 是信号子空间， $U_O$ 是噪声子空间。

第二步，定义误差相关矩阵 $R_A$

$R_A=R-{\sigma }^{2}I=AS{A}^H=U_A{\sum }_A{U}_A^H$ (14)

$R_A^{+}={\left(AS{A}^H\right)}^{+}=U_A{\sum }_A^{-1}{U}_A^H$ (15)

第三步，抛弃权矢量在噪声子空间中的分量，可得到新的权值：

$Wss=R_A^{+}{W}_0$ (16)

第四步，利用新的权值矢量，进行变步长LMS运算，即可实现自适应波束形成。

由于SS-VSLMS算法引入了新的函数，并且提取了权矢量在信号子空间中的分量，去除了干扰较大的特征矢量，能够提高自适应波束形成方法性能，具有较好的波束保形能力。

5. 数值分析

波束方向图

设置如下仿真参数：天线阵为64阵元均匀线阵，阵元间距为半波长，信道为AWGN，DOA分别取信源方向：−20，干扰方向：30，分别仿真出LMS算法、VSLMS算法、本文提出的SS-VSLMS算法在信噪比分别为−20 dB和20 dB时的波束方向图，如图4所示。由图可知，变步长的VSLMS算法和本文提出的SS-VSLMS算法的抗干扰性能比固定步长的LMS算法抗干扰能力强；低信噪比时，VSLMS算法和SS-VSLMS算法的抗噪声和波束保形能力差不多，但本文提出的SS-VSLMS算法的旁瓣更低；高信噪比时，VSLMS算法和本文提出的SS-VSLMS算法的抗噪声和波束保形能力趋向一致。

算法收敛曲线

以迭代次数为横轴，以均方误差为纵轴，绘制出的算法收敛曲线如图5所示。由图可知，固定步长的LMS算法大约要经过1000次迭代后达到收敛，基于S函数的VSLMS算法大约要经过600次才能达

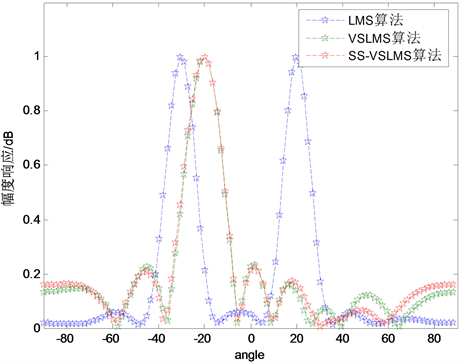(a) SNR = 20 dB 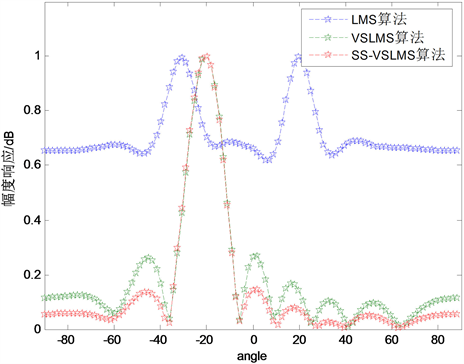(b) SNR = −20 dB

Figure 4. Beam pattern

图4. 波束方向图

Figure 5. Comparison of algorithm convergence curves

图5. 算法收敛曲线对比

到收敛，本文提出的SS-VSLMS算法只需经过100次就能达到收敛。结果表明，在同样的条件下，SS-VSLMS算法收敛速度最快。

6. 结论

波束保形(是指当存在强外干扰时，有时需要算法在达到抗干扰要求的前提下，新方向图与原方向图(也称静态方向图)尽量接近)、抗干扰、收敛速度是衡量LMS自适应波束成形算法性能的三个重要的指标。根据上一节对三个算法的三大性能的数值仿真分析可知，定步长LMS算法在这三个重要指标之间无法做到兼顾，变步长的VSLMS算法和本文提出的SS-VSLMS算法的波束保形和抗干扰能力基本相同，但本文提出的SS-VSLMS算法的收敛速度远高于VSLMS算法。总体上，本文提出的SS-VSLMS自适应波束形成具有更优越的性能，可兼顾多个性能指标，具有较好的实时性。这主要得益于以下两点改进：1) 本文提出的SS-VSLMS自适应波束形成算法基于非线性对数函数模型，这是对LMS算法基于S形函数的改进；2) 本文提出的SS-VSLMS自适应波束形成算法，仅保留权矢量中的信号子空间分量，这是对VSLMS算法权矢量的改进。