1. 引言
社会经济的快速发展,给人们带来了巨大利益的同时,也使得能源短缺与环境污染日益严峻,因此需要采用更加灵活、经济、环保的输配电方式来应对新的挑战。电压源换流器型直流输电(Voltage Source Converter-High Voltage DC, VSC-HVDC)的技术优势使其在可再生能源并网、无源网络供电、城市电网供电、异步交流电网互联等领域都发挥了积极作用 [1] [2] [3] ,但目前已投运的VSC-HVDC多采用两电平或三电平VSC拓扑结构,其拓扑结构受IGBT开关器件承受功率、电压承受能力的影响大,难以提高输电容量 [4] ,很大程度上限制了HVDC在高压、大功率场合的应用前景。针对传统多电平拓扑结构存在的问题,近年来提出一种新型的拓扑结构——模块化多电平换流器,因其独特的结构优势受到了广泛的关注,对基于MMC的直流输电系统的应用进行了深入研究,MMC子模块直接串联在桥臂中,彼此之间没有相互连接,抑制和减小电容电压的波动是保证MMC安全可靠运行的关键,因此需要采取相应的电容电压控制策略,保证电容电压的均衡。对子模块均压的控制,目前国内外对MMC换流器的控制策略进行广泛的研究,并取得了一些研究成果。文献 [5] 利用排序法对子模块进行均压,但该方法使MMC开关频率大,且随着子模块数量的增多,计算量会变得很大,文献 [6] 提出设置保持因子的MMC电容电压平衡控制,将排序重点放在越限的子模块上,降低了IGBT的开关频率。文献 [7] 提出一种希尔排序的算法,很大程度上减小了排序的次数,但是对于希尔排序的时间复杂度分析十分困难。文献 [8] 提出一种通过比较平均值的控制算法,此方法不需要对子模块进行排序,大大增加了计算速度,但对处于最值的两个子模块难以优先投切,且不易选取和配合。文献 [9] 提出了一种不需排序的模型预测控制方法,但是预测过程难以计算,而且只能在子模块不多的场合使用。文献 [10] 利用质因子分解的数学方法,提出一种分层分组的控制策略来减少排序的计算量,提高计算的速度,但组间电压难以均衡,导致均压效果的降低。
为了降低换流器运行时的开关频率,提高运算速度并能够保证其具有良好均压效果,本文以最近电平逼近调制(Nearest Level Modulation, NLM)策略为基础提出一种改进的电容电压均衡控制方法,该方法能够在电容电压均衡的前提下,一定程度降低排序次数,减少换流器开关损耗。
2. MMC基本工作原理
如图1为模块化多电平换流器的拓扑结构。由三相对称的三个结构相同的相单元构成换流器,每相
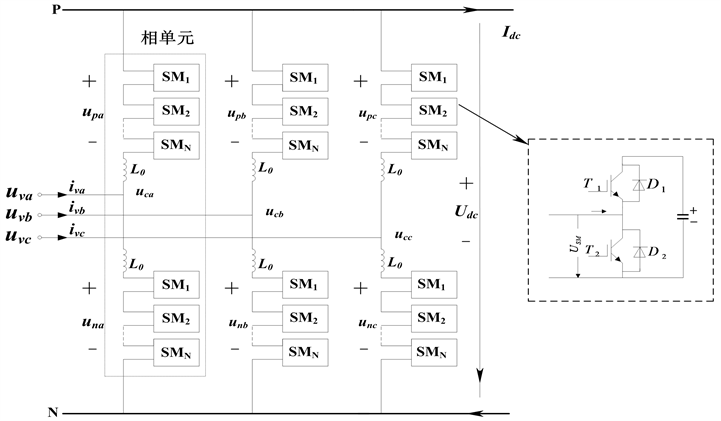
Figure 1. The topological structure of MMC
图1. MMC拓扑结构
的上、下两个桥臂构成一个相单元,每个换流器有6个桥臂组成,桥臂由一个电抗器
和若干个同样结构的子模块(Submodule, SM)串联组合而成,每个子模块由两个带反并联二极管的绝缘栅双极晶体管IGBT串联后与一个储能电容器并联组成。
、
、
分别表示网侧交流系统三相交流输入电流,
、
、
分别表示网侧三相交流输入电压,
为直流侧的输出电压,
为直流侧的输出电流。
通过给IGBT施加不同控制信号,每个子模块有闭锁、投入、切除三种不同的工作方式:第一种工作方式是全控型开关IGBT (T1, T2)全部关断,子模块处于闭锁状态。此时,无论
的方向如何,只能对SM进行充电,不能被放电,这种工作状态仅存在于MMC启动时对MMC预充电,或者发生故障时将子模块旁路;第二种工作方式是T1导通,T2关断,子模块处于投入状态,通过
流动方向的不同,对子模块进行充放电,这种工作方式是MMC的正常工作状态;第三种是T1关断,T2导通,子模块处于切除状态。此时无论
的方向如何,电容器都被旁路,输出电压都为0。这种工作状态不影响子模块的电容电压,对SM的冗余设计具有积极意义。
调制方式的差异对MMC的输出性能有着关键的影响,因此选择一个简单、高效、合适的调制策略至关重要。目前国内外学者提出了多种适用于MMC的调制策略,常见的调制策略主要有特定谐波消去脉宽调制、载波移相脉宽调制、载波层叠调制、电压逼近调制等 [11] 。在高压大功率柔性直流输电系统中,为满足要求,MMC桥臂中往往含有几十或数百个子模块,此时,使用PWM方式实现复杂,开关频率高,损耗较大。又因数目众多的子模块输出电平较高,交流侧电压波形的谐波含量已经较低,故使用控制方法更为简单,计算量更低的NLM更有优势。
NLM调制策略是通过控制正弦调制波的瞬时值来对控制上、下桥臂子模块的投入个数,使得在每一时刻交流侧产生的交流电压接近调制波,尽量使它们的差值最小。原理如图2所示,图中
表示正弦调制波,
表示子模块的平均直流电压值,任何时刻各相投入的子模块为N,如果上、下桥臂各自选取相等数目的子模块投入运行,则这种情况下相单元的输出电压为0。
由图可知,随着调制波从0开始逐渐变大,下桥臂子模块投入个数呈增加趋势,上桥臂子模块的投入个数的变化趋势与之恰好相反,
值越小越好,方波与调制波的拟合度越高,NLM的效果就越好。
在任意时刻,上下桥臂所要投入子模块的数目为式(1):
(1)
3. 电容电压均衡控制
3.1. 电容电压控制流程
传统电容电压控制的算法核心环节就是排序法,其控制原理是:首先根据调制波计算出需要投入运行的子模块个数,然后检测各子模块的电容电压值,并将其值进行排序,再对桥臂电流的极性进行检测,如果桥臂电流为正,那么此时子模块处于充电的状态,电容电压升高,将排序结果之中电压最低的N个子模块投入运行,如果桥臂电流为负,那么此时子模块处于放电的状态,电容电压降低,将排序结果之中电压最高的N个子模块投入运行。
传统电容均压方法简单,但在系统正常运行时,各桥臂电容会不断的进行充放电,即使只发生了很小的变化,就要全部进行排序,而子模块投切的频率非常高,大大增加了器件的损耗,影响其工作效率,这种情况在电平数越高的时候,损耗越大。但事实上,在MMC运行过程中,只要保持子模块电压的波动在一定范围之内就能保持输出侧波形的质量,而不必要把每一个子模块电压都严格保持在某个定值。
为减小IGBT的开关次数,降低开关损耗,本文提出了一种改进的电容电压均衡控制方法。该算法的原理认为在一定的波动区间的电容电压是稳定的,系统并不需要每时每刻对桥臂电容进行排序就可以保证电容电压的均衡,不影响换流器电压电流波形,这样大大减少了子模块的开关频率,提高了系统的运算速度。
其均衡控制图如图3所示。
改进均衡控制的基本思路是:首先确定电容的参考电压
与电压的偏移量
,在电压偏移量之内,认为电容电压是平衡的,不需要进行调节,当超出电压偏移量时,则根据
与
的大小进行优先充放电。对电容电压进行检测,若
,则将
赋值到B区间并计数为
,若
且
,则将
赋值到A区间并计数为
,电容优先充电,若
且
,则将
赋值到C区间并计数为
,电容优先放电。调制波计算出需要投入的子模块个数为n,判断桥臂电流,如果为正方向,则对子模块进行充电,若
,则A、B区间内子模块需要全部投入,C区间内投入
个子模块,若
,则A区间内子模块需要全部投入,B区间内投入
个子模块,若
,则在A区间投入n个子模块即可;如果为负方向,则对子模块进行放电,若
,则B、C区间内子模块需要全部投入,A区间内投入
个子模块,若
,则C区间内子模块需要全部投入,B区间内投入
个子模块,若
,则在C区间投入n个子模块即可。
3.2. 优化算法的参数的确定
通过第二章MMC工作原理的分析可知,六个桥臂分别可以用一个可控的电压源来等效替换,如图4即为MMC三相等效电路图。
MMC三相对称,故以A相为研究对象,假设:
(2)
(3)
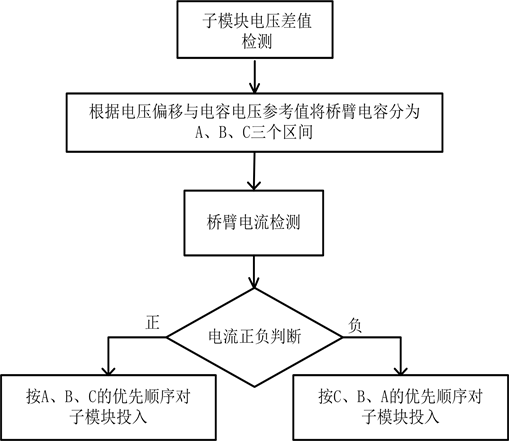
Figure 3. The block diagram of sub module balance control
图3. 子模块均衡控制框图
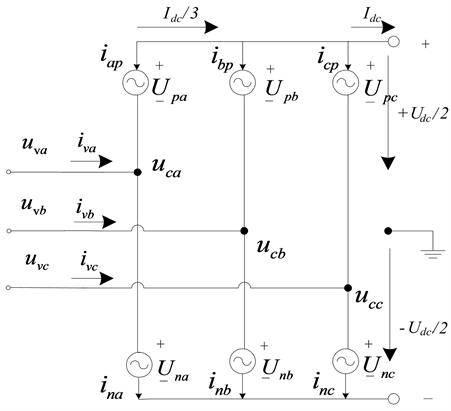
Figure 4. The equivalent circuit diagram of MMC
图4. MMC等效电路图
其中,
为输出相电压峰值;
为输出线电流峰值;
功率因数角。
便于分析,定义MMC电压调制比为 [12] :
(4)
定义MMC电流调制比为:
(5)
忽略MMC内部损耗时,由功率守恒可知MMC换流器输入功率等于输出功率,即:
(6)
结合式(4)、式(5)、式(6)可得:
(7)
理想情况下,由基尔霍夫定律可得MMC上、下桥臂电压为:
(8)
上、下桥臂电流为:
(9)
其中,
为基波角频率。
MMC上、下桥臂投入运行的子模块个数为:
(10)
因此,上、下桥臂开关函数可表示为:
(11)
由式(9)、式(10)、式(11)可得:
(12)
其中,
和
分别为MMC上、下桥臂子模块电容电压值。
上、下桥臂的子模块电容电压分别表示为 [13] :
(13)
其中:
为子模块电容电压额定值;
分别为基频波动和二倍频波动的幅度;
分别为其初相角。
对式(13)两侧分别求导,得:
(14)
对比式(12)和式(14),基频波动分量和二倍频波动分量的幅值应该分别相等,可得:
(15)
其中,
表示求取模值。
当忽略MMC的冗余条件时,
,因此可由式(15)反解出子模块电容电压基频波动与二倍频波动的幅度大小,即:
(16)
其中,S为MMC视在容量。
由此可知,该控制策略对电容的参考电压
电压的偏移量
的选择非常重要,电压的偏移量
选取过大或者过小都会影响对子模块子模块的优先充放电的投入。
电容的参考电压
的确定可以参考直流电压,由MMC拓扑结构可得:
(17)
由以上分析以及式(16)可知,当调制比
,
时,可以得出MMC子模块的最大波动量为:
(18)
故由式(18)可得电压的偏移量
为:
(19)
其中,
为调制系数,
。
4. 仿真验证
为了验证电容电压均衡控制的有效性,在PSCAD/EMTD中搭建了21电平的MMC-HVDC系统仿真模型,基本结构如图5所示。
其基本仿真参数如表1所示。
模型中每相上、下桥臂各有20个子模块,仿真中采用NLM调制策略,MMC1采用定直流电压和定无功功率控制,MMC2采用定有功功率和定无功功率控制,通过仿真可得MMC在稳态运行时改进均压控制结果如图6所示。
由图6(a)可以看出,采用改进的均压控制之后,子模块电容电压虽然有一定的波动,但是其仍具有较好的一致性,并且大小稳定在参考值25 kV上下;由图6(b)可以看出MMC换流器电平叠加后输出直流母线电压稳定在500 kV上下,从而验证了本文提出的改进的控制方法能够实现电容电压的均衡控制。
对于子模块的工作状态,其触发脉冲如图7所示。通过对图7(a)与图7(b)的仿真结果比较可知,采用优化控制策略后,子模块的开关频率较传统方法明显降低,减少了IGBT频繁开关造成的损耗,表明本文的均压控制是有效的。

Table 1. Model parameters in MMC-HVDC model
表1. MMC-HVDC系统模型参数
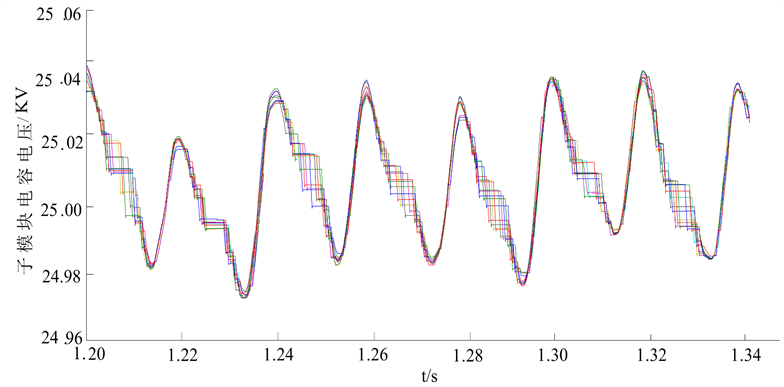 (a) 子模块电容电压
(a) 子模块电容电压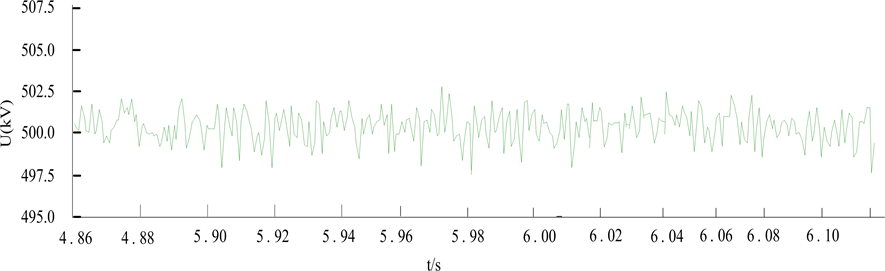 (b) 直流母线电压
(b) 直流母线电压
Figure 6. The improved simulation results of pressure mean control
图6. 改进均压控制仿真结果
 (a) 传统控制策略的触发脉冲
(a) 传统控制策略的触发脉冲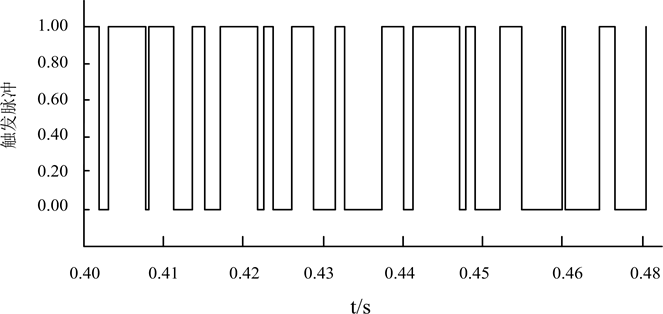 (b) 优化控制策略的触发脉冲
(b) 优化控制策略的触发脉冲
Figure 7. Comparison of the upper IGBT firing pulses
图7. IGBT触发脉冲比较
5. 结论
本文提出了一种改进的电容电压均衡控制方法,该方法认为在一定的波动空间内电容电压是稳定的,不需要时刻对电容电压进行排序,这样就可以使子模块开关器件尽量的保持原来的开关状态,能够在较低的计算量下完成对电容电压的均衡控制,一定程度上能够降低开关器件的频率和系统损耗。并在PSCAD/EMTDC仿真平台上搭建了MMC-HVDC模型,对本文设计的电压均衡控制的有效性进行验证,结果表明本文设计的控制策略可以在较低频率下实现电压的均衡控制。