1. 引言
根据配电网合环操作的研究资料,负荷转供作业的风险主要来自于合环操作引起的线路电流变化 [1] ,合环后线路电流有可能因为超过设备容量限额或不能满足继电保护要求导致继电保护动作进而影响电力系统供电可靠性 [2] 。因此研究合环引起的循环电流计算方法以及提出能有效降低循环电流的措施对负荷转供作业具有重要意义。
目前我国对循环电流计算的一般方法是将合环系统等效成戴维南电路,电路中的等效电源为合环点两侧电压相量差,等效阻抗为从合环点两侧节点往系统上级看进去的等效阻抗 [3] 。由于合环点两侧电压相量差可以通过SCADA数据采集系统直接获取,因此循环电流的计算难度主要在等效阻抗上。目前一般是通过电力系统调度部门提供网络节点阻抗参数,再由合环点两侧节点的自阻抗减去互阻抗近似求得 [4] 。该方法虽然简单快捷,但是考虑系统的运行方式会有变更,该方法不能实时计算出准确的系统等效阻抗,因此本文重点研究满足工程实时测量需求的系统等效阻抗测量方法。
在计算出循环电流后,若循环电流大小不满足作业条件,则需要采取一定的有效措施降低循环电流。研究表明影响循环电流的主要因素包括合环点两侧电压相量差、主变参数、线路参数以及合环点两侧出线所带负荷的情况 [5] 。针对合环点两侧电压相量差因素,目前调整变压器分接头法是最为常用和有效的方法 [6] 。对于一个实际的配电网络,其网络中的主变和线路参数已经选定,因此本文重点研究通过负荷控制实现循环电流的降低。目前国内针对负荷控制提出的一般策略为在负荷低谷期进行合环 [7] 。实际操作中该策略要求合环时刻选取在当地负荷低谷时段,作业需要考虑时间条件的配合,不适用于急需合环的作业情况。
为了解决上述问题,本文建立了配网合环等值电路图,研究能实时测量系统等效阻抗并计算合环循环电流的方法,并基于潮流的计算分析研究了负荷对出线上循环电流的影响,提出了通过降低负荷功率以提高合环点两侧负荷对称性的负荷控制策略。并通过MATLAB/Simulink软件进行了仿真和计算,仿真结果表明所提的循环电流计算方法是正确的以及降低措施是有效的。
2. 循环电流实时计算方法研究
为了满足负荷转供作业中实时计算循环电流的要求,本文提出基于叠加原理的电流注入法,该方法可以不需要通过形成节点阻抗矩阵Zn×n来计算等值阻抗,计算过程相比目前所用的节点阻抗矩阵法更加直观且满足实时性。基于叠加原理的电流注入法等效图如图1所示。
实际测量中系统处于运行状态,网络中的电源和负荷均不为0。因此可首先测量保留网络原有电源和负荷的情况下合环点两侧节点a和b的节点电压Ua0和Ub0。在初始系统的基础上,保证其他节点均无电流注入的情况下在合环点两侧节点a和b处分别注入幅值相同,方向相反(即相角相差180˚)的电流,并再次测量节点a和b的节点电压Ua1和Ub1。由叠加定理可得,通过前两次的测量值相减可得到将系统中负荷和上级网络电源全部置0时的无源网络中注入电流的测量情况,进而求解得到等值阻抗与循环电流。计算表达式如下所示。
(1)
(2)
(3)
(4)
对本文所提基于叠加原理的电流注入法运用Matlab/Simulink进行仿真验证。仿真电路图如图2所示。

Figure 1. Equivalent circuit diagram of combined loop current calculation
图1. 循环电流计算等值电路图
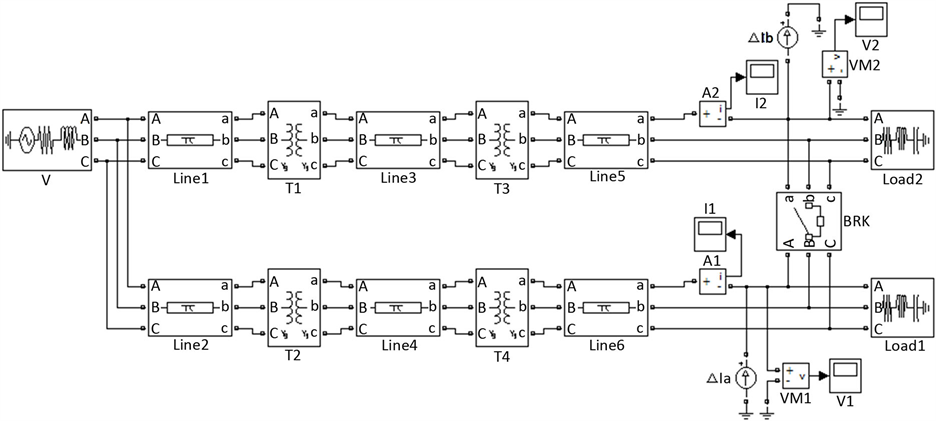
Figure 2. Simulation circuit diagram of circulating current calculation
图2. 循环电流计算仿真电路图
对仿真所得电压电流数据进行幅频求解获得计算所需的电压电流相量,本次仿真验证中,I循环的理论值为合环前后线路上电流的相量差,I循环的计算值为采用本文所提基于叠加原理的电流注入法的计算结果。所需电压电流的测量结果如表1和表2所示。循环电流计算结果如表3所示。
通过上表数据可知,I循环的计算值基本符合I循环的理论值,验证了本文所提的基于叠加原理的电流注入法计算合环循环电流的合理性。分析本次仿真的误差:一是仿真中电压数据是10 kV级别的,而软件仿真对节点电压数据只保留了5位有效数字,因此电压数据不够精确对本文的仿真结果造成了一定误差;三是本文在求取节点电压相量和馈线电流相量时是通过Matlab中的fft功能模块实现的,fft函数对波形数据进行幅频和相频的计算求解存在一定误差。
3. 合环操作影响判据
研究合环操作对系统运行的影响一般是基于线路上的合环稳态电流进行分析的 [8] 。研究表明合环后线路稳态电流为线路初始负荷电流与循环电流的叠加 [9] 。因此可以通过循环电流大小来初步判断合环操作对系统运行造成的影响程度。
4. 提高合环转供电成功率的应对措施
4.1. 负荷控制
为了减少合环操作引起的合环电流对电网系统造成的不利影响,控制系统中负荷是比较方便和有效的应对措施之一。系统中负荷主要包括母线负荷和线路负荷,一般对负荷的控制包括切除负荷以及基于

Table 1. Current phasor measurement values
表1. 电流相量测量值

Table 2. Voltage phasor measurement values
表2. 电压相量测量值

Table 3. Calculated values of circulating currents
表3. 循环电流计算值
负荷情况进行操作等。对简化所得的系统合环等值电路图进行潮流分析和计算 [10] 。
图3用于分析合环过程中功率潮流变化情况,图中UAH2,UBH2为合环开关闭合后变压器T1和T2的高压侧电压;SAH2,SBH2为合环开关闭合后流入变压器T1和T2的功率;变压器T1和T2的阻抗为ZT1,ZT2;SAL2,SBL2为合环开关闭合后流出变压器T1和T2的功率;UAL2,UBL2为合环开关闭合后变压器T1和T2的低压侧电压;SA,SB,SC,SD分别为母线负荷和出线负荷;ΔS为由节点a流向节点b的功率。在对该系统进行潮流计算时需要结合负荷转供作业形成环网所带来的相关参数边界条件 [11] 。则合环开关闭合后,变压器T1和T2的高压侧母线电压如式(5)和式(6)所示。
(5)
(6)
考虑合环开关所在出线的阻抗很小可忽略不计,则合环开关闭合后变压器T1和T2的低压侧母线电压差为0,即UAL2 = UBL2 = UL2,因此合环开关闭合后,变压器T1和T2的高压侧母线电压差ΔUH2如下。
(7)
流入系统的总功率S以及由节点a流向节点b的功率ΔS以及循环电流的计算公式如下 [12] 。
(8)
(9)
(10)
(11)
将式(8)、式(9)和式(10)代入式(7)中,并结合式(11)可以求得合环操作引起的环网中循环电流如下。
(12)

Figure 3. System closed-loop flow analysis diagram
图3. 系统合环潮流分析图
目前现有文献所提减小合环电流的负荷控制方法基本是建立在切除负荷或者考虑在负荷低谷期进行合环的基础上。当合环点两侧负荷参数满足某些情况时,切除负荷的控制方法是不能起到减小合环电流的作用,甚至会使合环电流增大。另外,考虑在负荷低谷期合环的方法,即合环开关两侧所带负荷均减小,通过式(12)可知,当SA,SB,SC,SD均减小时,可以使该式分母参数减少,进而实现合环电流的减小。但该方法要求当地负荷低谷时刻接近合环点合环时刻,所需条件较为苛刻。
考虑系统中变压器型号和参数已经固定,ZT1和ZT2为固定值,重点研究负荷参数。分析式(12)可知,合环开关两侧所带负荷,包括母线负荷以及馈线负荷的对称性越高,即(SA + SC)与(SB + SD)越相近,则合环操作后引起的合环电流越小,实际操作中可先测得合环点两侧负荷功率大小,通过适当的投切负荷提高合环点两侧负荷对称性。
4.2. 负变压器分接头调整
调整变压器分接头是调节合环电流比较有效也是最为常用的方法。当系统的运行方式和配网侧负荷确定以后,影响合环过程中合环冲击电流以及合环稳态电流大小最主要的因素是合环开关两侧电压幅值差和相角差,由于目前没有较好的电压相角差控制方法,所以主要通过调整变压器分接头控制合环开关两侧电压幅值差,进而减小合环电流以保证合环过程的安全成功性。
调整变压器分接头调节合环电流的基本原则是:在合环操作前,运用潮流计算或者测量系统获得合环点两侧10 kV低压母线的电压相量值,将母线电压幅值较低的一侧变比调低或者将母线电压幅值较高的一侧变比调高,使合环点两侧变压器低压侧母线上的电压幅值接近。假设合环操作前,合环开关两侧电压相量分别为
和
,考虑进行变压器分接头调整后,合环开关两侧电压相量幅值发生变化而角度不变,相角差为
,作出电压调整的相量图,如图4所示。
U1和U2为合环操作前合环开关两侧电压,对U1所属线路上的110 kV/10.5 kV变压器进行分接头调整,即U1可在其相量延长线上变化,U2保持不变。在对U1进行电压幅值调整时,影响合环电流大小的因素是电压相量差ΔU,因此应该以U2在U1相量上的投影U1t为准进行调整,此时合环点两侧电压差拥有最小值ΔUmin,分接头调整公式如下所示。
(13)
5. 仿真与分析
5.1. 负荷控制仿真
控制系统中负荷为单一变量并进行仿真可以分析负荷控制与循环电流大小的关系。本文仿真中负荷支路分布如图5所示。负荷1和负荷2为合环开关两侧出线所带负荷,负荷3和负荷4为合环开关两侧母线所带负荷。出线负荷功率如表4所示。
本例中,合环点左侧母线负荷与出线负荷之和为13 + j4.5 MV·A,合环点右侧母线负荷与出线负荷之和为18 + j7.5 MV·A。根据前文所述通过控制负荷减小循环电流原理可知,合环点两侧负荷对称性越高,合环过程引起的循环电流越小。为使本例中合环点两侧负荷趋于对称,可以通过控制出线负荷1的有功功率提高,出线负荷1的无功功率提高,出线负荷2的有功功率降低,出线负荷2的无功功率降低四种方式实现。利用Matlab/Simulink软件对负荷控制方式进行仿真,分析负荷调整方法对合环转供电过程的影响以验证本文所提方法。负荷控制对循环电流影响的Matlab/Simulink仿真图如图6所示。
5.1.1. 负荷1有功功率控制
保持其他负荷节点负荷功率不变,控制馈线负荷1的有功功率提高,从1 MW提高到2 MW,每次
取样的仿真步长为0.1 MW,记录负荷调整过程中冲击电流和循环电流的大小,如表5所示。馈线负荷1的有功功率提高与冲击电流和循环电流大小变化关系如图7所示。
5.1.2. 其他负荷功率控制
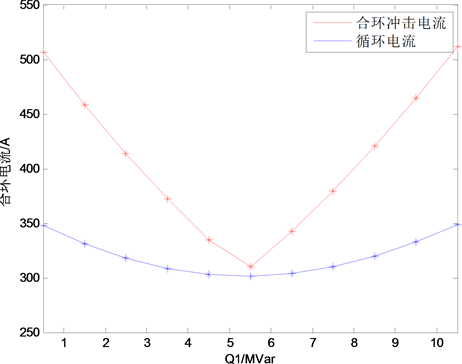
保持其他负荷节点负荷功率不变。分别控制馈线负荷1的无功功率从0.5 MVar提高到1.5 Mvar;控制馈线负荷2的有功功率从3 MW降低到2 MW;控制馈线负荷2的无功功率从1.5 Mvar降低到0.5 Mvar。上述三种控制方法下负荷功率控制过程中冲击电流和循环电流变化关系如图8所示。
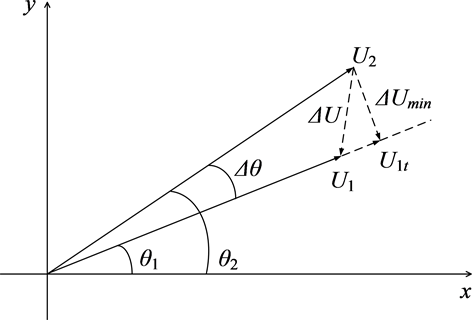
Figure 4. Voltage phasor diagram for transformer tap adjustment
图4. 变压器分接头调整的电压相量图

Figure 5. Load control simulation simplified diagram
图5. 负荷控制仿真简化图
5.1.3. 仿真步长为1 MW下的功率控制
根据上述仿真结果可知:通过控制馈线负荷1的有功功率提高,馈线负荷1的无功功率提高,馈线负荷2的有功功率降低,馈线负荷2的无功功率降低四种方法使合环点两侧负荷趋于对称,能有效降低合环操作过程中的循环电流,验证了本文所提通过提高合环点两侧负荷对称性的负荷控制方法的合理性。考虑增加仿真步长,以负荷1的功率控制为例,功率调节步长提高至1 MW和1 MVar,记录负荷调整过程中冲击电流和循环电流的大小。负荷1的功率提高与冲击电流和循环电流大小变化关系如图9所示。

Table 5. Load 1 circulating current in active power control process
表5. 馈线负荷1有功功率控制过程中的冲击电流和循环电流
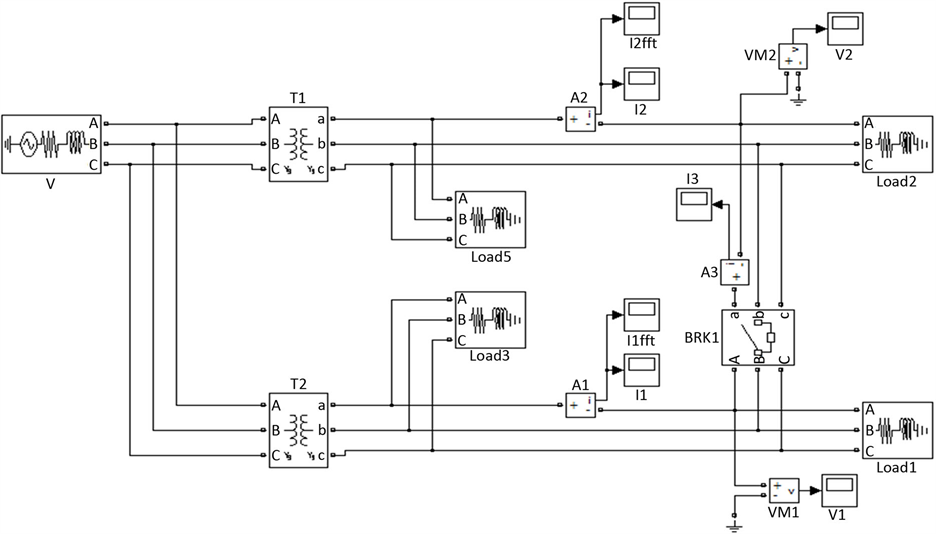
Figure 6. Load control simulation circuit diagram
图6. 负荷控制仿真电路图
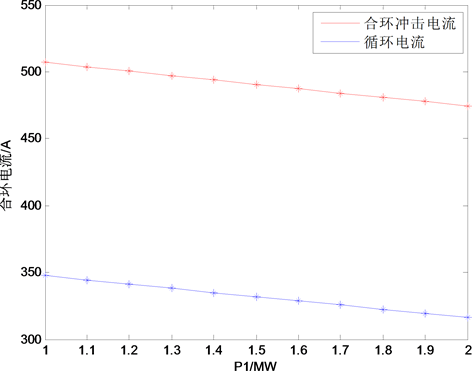
Figure 7. Load 1 active power control
图7. 负荷1有功功率控制
 (a)
(a) 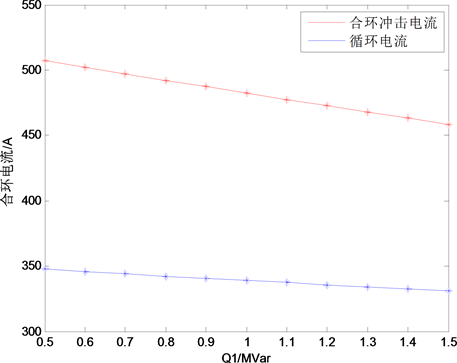 (b)
(b)  (c)
(c)
Figure 8. Other load power control; (a) Load 1 reactive power control; (b) Load 2 active power control; (c) Load 2 reactive power control
图8. 其他负荷功率控制;(a) 负荷1无功控制;(b) 负荷2有功控制;(c) 负荷2无功控制
 (a)
(a) 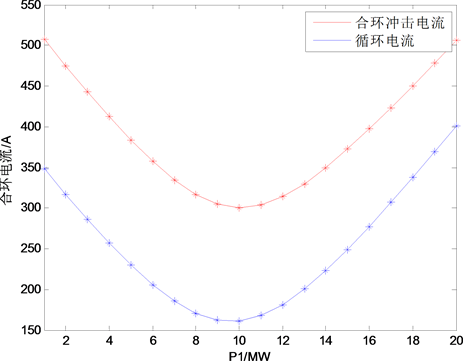 (b)
(b)
Figure 9. Load 1 power control (a) Load 1 active power control; (b) Load 1 reactive power control
图9. 负荷1功率控制(a)负荷1有功控制;(b)负荷1无功控制
由仿真结果分析可知,当馈线负荷1有功功率调整至10 MW时,合环后线路上冲击电流最大瞬时值与稳态循环电流值达到最小。当馈线负荷1有功功率继续上调时,循环电流增大。符合本文所提的提高合环点两侧负荷对称性的负荷控制方法。但考虑实际操作中负荷投切量的大小不可能达到1 MW等级 [13] ,因此0.1 MW和0.1 Mvar仿真步长下的数据更符合实际操作,对实际运行更具指导意义。在实际运行中,进行负荷转供作业的两条10 kV出线会形成一个总负荷 [14] 。以图4为例,该总负荷即等于S1 + S2 + S3 + S4,如果这个总负荷超过一个定值范围则会导致合环环流增大从而造成线路过载。所以,在负荷转供作业准备过程中需要注意对两条线路总负荷的核算和调整,将其控制在合理范围内。另外,通过增加负荷以达到提高对称性的方式虽然能降低循环电流,但出线上的初始负荷电流也会增加 [15] 。因此一般尽量选择减负荷以达到提高合环点两侧系统负荷对称性的方式或者不建议在本地负荷高峰期进行合环操作。
5.2. 变压器分接头调整仿真
在仿真中,由于合环点两侧电压可直接通过电压测量元件测得,不需要通过复杂的潮流计算求解,因此可以直观的研究变压器分接头调整方法对降低合环电流的影响。本次仿真中,系统初始状态下变压器分接头参数采用表6所示的初始变比进行合环操作仿真,获得初始变比下合环电流数据。然后调整变压器分接头,即改变变压器变比,再重新进行合环操作仿真,并记录此时合环电流数据,将分接头调整过程的合环电流数据进行对比和分析,并将数据记录于表7中。分接头调整过程合环冲击电流大小和循环电流大小分别如图10所示。
变压器分接头设置为初始变比110kV/10.5 kV时,合环操作前合环开关两侧馈线电压U1和U2分别为8.7452∠−92.77˚和8.6281∠−93.99˚,代入式(13)中可求得分接头要选取111.375 kV/10.5 kV。在该变比下,电路中的合环冲击电流和循环电流最小,验证了通过调整变压器分接头减小合环电流方法的合理性。
6. 结论
1) 本文所提基于叠加原理的电流注入法测量系统等效阻抗,进而计算合环操作引起的循环电流具有实时性和直观性的优点。
2) 通过采用提高合环点两侧负荷对称性的负荷控制策略,特别是以减负荷达到提高对称性的方式,能有效降低合环操作引起的循环电流大小,进而降低合环操作的风险,提高作业过程中系统运行的安全

Table 6. Transformer tap changer parameters
表6. 变压器分接头参数

Table 7. Loop current in the tapping process
表7. 分接头调整过程合环电流大小
稳定性。
3) 通过合理调整变压器分接头,控制合环开关两侧电压幅值差,能有效减小合环电流,提高合环成功率。
4) 本文对合环操作中降低循环电流的研究中提出了合理的负荷控制策略,实际工程中可以通过投切电容器或电抗器等措施实现,今后应对这些具体的负荷控制措施的实施过程及其对系统安全稳定的影响做深入研究。另外在变压器分接头调整的研究中可知合环点两侧电压相角差也是影响循环电流的重要因素之一,目前国内没有较好的解决办法,因此今后应该重点研究降低合环点两侧电压相角差的有效措施。