1. 引言
考虑如下具变号权函数的多参数二阶微分系统:
(1)
其中,
是两个参数,且
在
上可能变号。
令
,且
和f分别满足如下条件:
(H1)
是连续的,且存在
使得
且
在J的任意子区间上不恒为零;
(H2)
是连续的,且当
时,
;
(H3) 存在
和
使得
;
(H4) 存在
,使得
。
其中,
。
当
时,系统(1)退化为Wang和An在文献 [1] 中研究的问题,利用不动点定理得到了该问题至少存在一个正解和两个正解的充分条件。但是,在文献 [1] 中,Wang和An只考虑了
恒为1的情况,本文则考虑
时的情况,并且得到了系统(1)至少存在三个正解的结果。
在过去的几十年中,对于权函数不变号的二阶微分方程问题,众多学者进行了研究并取得很多成果 [2] - [7] 。例如,在文献 [5] 中,卢和冯研究了具偏差变元的二阶微分方程边值问题,并得到了三个正解的存在性。但是在这些文献中,作者都没有考虑权函数变号的情况,而对具变号权函数的微分方程边值问题的研究,在物理中有一定的意义。比如,量子力学、半导体理论以及核反应中的一些数学模型都可以归结为具变号权函数的微分方程问题 [8] [9] [10] 。因此,这类问题受到了越来越多的学者的关注,并获得了一些优秀成果 [11] - [17] 。文献 [11] 中,Jiang和Yao研究了如下半线性两点边值问题
正解的存在性。其中,
在
上可能变号。作者运用Schauder不动点定理给出了上述问题正解存在性定理。
但是到目前为止,关于含参数的具变号权函数二阶微分系统多个正解的存在性的研究还不多见。本文致力于研究具变号权函数的多参数二阶微分系统存在多个正解的充分条件。
2. 预备知识
定义
则有
系统(1)等价于下列两个边值问题:
(2)
和
(3)
定义2.1. 若
是系统(1)的一个正解,当且仅当
满足系统(1),且
,
。
引理2.1. 假设条件(H1)-(H2)成立,则
是问题(2)的一个解当且仅当u是下列积分方程的一个解
(4)
其中,
(5)
证明:引理2.1的证明类似于文献 [7] 中引理1.1的证明。□
由
的定义可知,它有如下性质:
命题2.1.
由(5)式定义,则有
引理2.2. 假设条件(H1)成立,则问题(3)有一个解
且
(6)
证明:引理2.2的证明类似于文献 [7] 中引理1.1的证明。□
由引理2.1和引理2.2可得下列引理2.3。
引理2.3. 假设条件(H1)~(H2)成立,则
是系统(1)的一个解当且仅当u是下列积分方程的解
(7)
且
满足(6)式。
为了获得系统(1)正解的存在性,需要假设下列条件成立:
(H5) 存在
使得
(H6) 存在
使得
(H7) 存在
使得
令
。对于
,
,
则
是一个Banach空间。
记
定义锥K如下:
(8)
对任意
,显然有
。
对于
,令
定义算子
如下:
(9)
由以上引理,我们可以得到引理2.4。
引理2.4. 假设条件(H1)~(H2)成立,则
是系统(1)的解当且仅当u是算子T的不动点且
满足(6)式。
引理2.5. 假设条件(H1)~(H7)成立,则
且算子
是全连续的。
证明:引理2.5的证明类似于文献 [1] 中引理2.2的证明。□
下面给出本文运用的主要引理,见文献 [18] 。
引理2.6. 设P是 Banach空间E上的一个锥,
是E中的有界开集,并且满足
。若算子
全连续,则当下述条件满足其一时,算子T在
上至少有一个不动点:
1)
2)
3. 主要结论
在本节中,我们运用引理2.6讨论系统(1)存在多个正解时的参数的最优区间。
定理3.1. 假设条件(H1)~(H7)成立。当
时,存在
,使得当
,
时,系统(1)至少存在两个正解。
证明:一方面,由于
,根据条件(H3),得
这表明存在
,使得
其中,
满足
,
。
令
(10)
选取
,则有
(11)
对任意
,有
,则
成立。进而有
即
(12)
令
(13)
另一方面,由于
,根据条件(H3),得
这表明存在
,使得
其中,
满足
且
(14)
如果
,由
在
上凹可得
(15)
进一步可得
(16)
选取
,则有
对任意
,由(16)式可得
和
即
(17)
最后,存在
,由条件(H2)可定义
令
(18)
其中,
。
则对任意
,有
和
因此,可得
(19)
取
。综上所述,由引理2.6可知,对任意
,(12)式和(17)式、(12)式和(19)式分别蕴含着T有一个不动点
满足
和
。又由引理2.4可知,系统(1)至少存在两个正解
。其中,
且
□
定理3.2. 假设条件(H1)~(H7)成立。当
时,存在
,使得当
,
时,系统(1)至少存在两个正解。
证明:一方面,由于
,根据条件(H3),得
则存在
,使得
其中,
满足
。其中,
在(13)式中定义,
在(14)式中定义。
因此,对任意
,由(16)式可得
和
即
(20)
另一方面,由于
,根据条件(H3),得
则存在
,使得
其中,
满足
,
在定理3.1中定义。
由条件(H2),可得
,则有
令
则可验证对于充分小的
,
是合理的。因此,对任意
,可得
即
(21)
令
其中,
,
在定理3.1中定义。
则对任意
,类似于(21)式的证明,可得
即
(22)
综上所述,由引理2.6可知,对任意
,
,(20)式和(21)式、(20)式和(22)式分别蕴含着T有一个不动点
满足
和
。又由引理2.4可知,系统(1)至少存在两个正解
。其中,
且
□
定理3.3. 假设条件(H1)~(H7)成立。当
时,存在
,使得当
,
,
且
满足
时,系统(1)至少存在三个正解。其中,
在定理3.1中定义。
证明:首先,由于
,根据条件(H3),得
则存在
,使得
其中,
满足
。其中,
在(13)式中定义,
在(14)式中定义。
因此,对任意
,与(20)式的证明相同,可得
(23)
其次,选取充分大的
,则有
。
对任意
,有
即
(24)
再次,由于
,根据条件(H3),得
则存在
,使得
存在
,满足
则对任意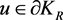 ,可得
,可得
即
(25)
最后,选取
。由条件(H2)可得
。
令
则对任意
,有
即
(26)
综上所述,由引理2.6可知,对任意
,(24)式和(25)式、(23)式和(25)式、(23)式和(26)式分别蕴含着T有一个不动点
满足
,
和
。又由引理2.4可知,系统(1)至少存在三个正解
。其中,
且
□
4. 例子
例4.1. 考虑如下二阶微分系统:
(27)
其中,
且
结论:当
,
时,系统(27)至少存在两个正解。
为了验证满足定理3.1的条件的成立,根据文献 [2] 的命题2.3,我们给出以下命题:
命题4.1. 考虑如下问题
其中,
,
满足
且
如果存在
使得
(28)
则下列不等式成立
(29)
例4.1的证明:由
,
和
的定义可知
。下面来验证定理3.1的条件成立。
首先,条件(H1)~(H4)显然成立。其次,分三步验证条件(H5)~(H7)成立。
第一步验证条件(H5)的成立。令
,
和
,(28)式等价于下列不等式
令
。则上述不等式等价于
由
的定义可得上述不等式成立,则条件(H5)成立。
第二步验证条件(H6)的成立。令
,
,
和
,则(29)式为
另外,由上述不等式可得
即由上述不等式可得条件(H6)的成立。
与第一步的证明类似,(28)式等价于下列不等式
由
的定义可得上述不等式成立,则条件(H6)成立。
第三步验证条件(H7)的成立。令
,
,
和
,与第一步的证明类似,(28)式等价于下列不等式
由
的定义可得上述不等式成立,可得条件(H7)成立。因此,条件(H1)~(H7)成立。
最后,由计算可得
取
,
,则
取
,可得
。则
。
综上所述,由定理3.1可得,当
,
时,系统(27)至少存在两个正解。
例4.2. 考虑如下二阶微分系统:
(30)
其中,
,且
定义与例4.1中相同。
结论:当
,
时,若
满足
,则系统(30)至少存在三个正解。
例4.2的证明:类似与例4.1的证明,条件(H1)~(H7)成立。
取
,则
,
。由定理3.3可得,若
满足
则系统(30)至少存在三个正解。
基金项目
国家自然科学基金面上项目(11471146),北京市教育委员会专项(PXM2017_014224_000020)。