变化环境下水文模型时变参数的识别及函数型式构建

Identifying Functional Form of Time-Varying Hydrological Model Parameters under Changing Environment

摘要: 选用两参数月水量平衡模型，采用集合卡尔曼滤波算法识别水文模型参数时变过程，通过模型参数与气候因子的相关性分析，构建了参数与降水、潜在蒸散发和气温的线性函数。以美国MOPEX数据库的3个流域为研究对象，利用1983~2003年的月水文数据进行实例研究，结果表明：相较于常数参数方案，考虑时变型式参数的模型在率定期和检验期的径流模拟纳什效率系数可分别提高18%和17%，且对峰值的模拟更优；通过典型干旱年(1999~2001年)与湿润年(2003年)分析降水变化对径流的影响，发现以往将参数视为常数会低估径流的变化，低估量最高可达38%，而时变参数方案可将径流变化量误差降至7%。因此，将水文模型参数考虑为气候因子的函数型式更有利于变化环境下径流预测的准确性。

Abstract: A two-parameter monthly water balance model was chosen to establish the functional forms of model parameters. The ensemble Kalman filter technique was used first to identify the time-varying parame-ters, following the construction of the linear functions of parameters and precipitation, potential evapotranspiration and temperature via the correlation analysis between model parameters and climatic factors. The case study was carried out in three Model Parameter Estimation Experiment (MOPEX) catchments in USA using the hydrological data from 1983 to 2003, in which the periods from 1999 to 2001 were selected as droughty year, while 2003 was selected as wet year. The results indicated that: 1) The accuracy of runoff simulations was improved when considering the model parameters as time-varying, especially in peak flows. The Nash-Sutcliffe efficiency coefficient of runoff was increased by 18% and 17% for the calibration and validation periods, respectively; 2) the change of runoff was underestimated when considering the model parameters as constant, with the relative error being up to 38%, while its value was reduced to 7% when considering the model parameters as time-varying. Therefore, taking the hydrological model parameters as a function of climate factors led to a significant enhancement in runoff prediction under changing environment.

1. 引言

气候变化，尤其是降水变化，改变了陆地水循环的强度，造成流域水资源的变化 [1] 。水文模型是研究水文过程响应气候变化的重要途径，在解决水文实际问题与进行水文规律研究上都起到关键作用。水文模型参数直接影响水文模拟的准确性，目前对气候变化下的径流预测采用的模型参数都是定值，但实际情况下，参数会随气候条件和土地利用变化而发生改变 [2] [3] ，水文模型参数的时变性已得到国内外水文学者的极大关注。邓超等 [4] 利用数据同化技术将径流观测值同化入水文模型中，发现数据同化方法能准确地识别出不同情景的参数变化。采用数据同化方法识别参数无需事先知道参数的变化趋势，但由于参数估计依赖于本时段的观测值，因而该方法没有预测能力，不可用于未来的水文模拟 [5] 。因此，为研究变化环境下的径流变化，还需构建准确的时变参数函数型式。本研究针对该问题，通过构建参数与气候因子的函数型式，分别研究参数为时变及常数的情况下降水变化对径流的影响。

2. 研究方法

2.1. 两参数月水量平衡模型

采用熊立华等 [6] 于1996年提出的两参数月水量平衡模型，该模型具有结构简单、物理概念明确、参数较少等优点，已被广泛应用于流域中长期水文模拟 [7] [8] 。其中，月实际蒸发值的计算公式为：

$E{T}_t=C\times PE{T}_t\times \tanh \left(P_t/PE{T}_t\right)$ (1)

式中： $E{T}_t$ 为月实际蒸发值， $PE{T}_t$ 为月潜在蒸发值， $P_t$ 为月降水量。C为模型的一个参数，t表示月份。

月径流量与土壤含水量有密切关系，其计算公式为：

$Q_t=S_t\times \tanh \left(S_t/SC\right)$ (2)

式中： $Q_t$ 为月径流量， $S_t$ 为土壤含水量。SC为模型的第二个参数，定义为流域最大蓄水能力(mm)，代表当土壤几乎没有水分时整个流域的平均持水能力。

扣除蒸散发后的土壤含水量为 $S_{t-\text{1}}+P_t-E{T}_t$ ，将其代入公式(2)得：

$Q_t=\left(S_{t-1}+P_t-E{T}_t\right)\times \tanh \left[\left(S_{t-1}+P_t-E{T}_t\right)/SC\right]$ (3)

式中： $S_{t-1}$ 为第 $t-\text{1}$ 个月底，第t个月初的土壤含水量。由水量平衡原理，第 $t+\text{1}$ 个月初的土壤含水量计算公式为：

$S_t=S_{t-1}+P_t-E{T}_t-Q_t$ (4)

2.2. 集合卡尔曼滤波算法识别时变参数

集合卡尔曼滤波算法 [9] 是数据同化领域中的主流算法之一，已被广泛应用于时变参数的识别及径流过程模拟 [10] [11] 。它通过Monte-Carlo法计算状态的预报误差协方差，再利用观测信息对状态进行预报和更新。集合卡尔曼滤波算法的实现过程如下：根据水文模型选择状态变量和观测变量，构建加有误差扰动的状态方程和观测方程；初始化背景场，得到一组分析值后利用状态方程对下一时刻的状态值和参数值进行预报；计算协方差矩阵和增益矩阵，以及模型模拟值，加入观测信息以更新预报值得到下一时刻分析值。

通用的状态方程为：

$\left(\begin{array}{c}{\theta }_{i,k+1}^f\\ x_{i,k+1}^f\end{array}\right)=\left(\begin{array}{c}{\theta }_{i,k}^a\\ f\left(x_{i,k}^a,{\theta }_{i,k+1}^f\right)\end{array}\right)+\left(\begin{array}{c}{\delta }_{i,k}\\ {\epsilon }_{i,k}\end{array}\right),{\delta }_{i,k}~N\left(0,R_k\right),{\epsilon }_{i,k}~N\left(0,G_k\right)$ (5)

式中： $\theta$ 为参数变量，x为状态变量； ${\theta }_{i,k+1}^f$ 和 $x_{i,k+1}^f$ 是 $k+\text{1}$ 时刻第i个集合预测值， ${\theta }_{i,k}^a$ 和 $x_{i,k}^a$ 是k时刻第i个集合分析值；f是模型算子； ${\delta }_{i,k}$ 和 ${\epsilon }_{i,k}$ 是模型误差，服从均值为0，特定方差(R_k, G_k)的正态分布。

观测方程：

$y_{i,k+1}=h\left(x_{k+1},{\theta }_{k+1}\right)+{\xi }_{i,k+1},{\xi }_{i,k+1}~N\left(0,S_k\right)$ (6)

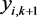式中：是 $k+\text{1}$ 时刻第i个集合的模拟径流值；h 是观测算子； ${\xi }_{i,k+1}$ 是服从正态分布的误差项。

更新过程：

$\left(\begin{array}{c}{\theta }_{i,k+1}^a\\ x_{i,k+1}^a\end{array}\right)=\left(\begin{array}{c}{\theta }_{i,k+1}^f\\ x_{i,k+1}^f\end{array}\right)+\left(\begin{array}{c}{K}_{k+1}^{\theta }\left[y_{i,k+1}-h\left(x_{i,k+1}^f,{\theta }_{i,k+1}^f\right)\right]\\ K_{k+1}^x\left[y_{i,k+1}-h\left(x_{i,k+1}^f,{\theta }_{i,k+1}^f\right)\right]\end{array}\right)$ (7)

式中： $K_{k+1}$ 是卡尔曼增益矩阵。

基于两参数月水量平衡模型的状态方程和观测方程如下，其中参数变量为模型的蒸散发参数C和流域最大蓄水能力SC，状态变量为土壤含水量S，观测变量为径流Q和实际蒸散发ET。

状态方程：

$\left(\begin{array}{c}{C}_{i,k+1}^f\\ S{C}_{i,k+1}^f\\ S_{i,k+1}^f\end{array}\right)=\left(\begin{array}{c}{C}_{i,k}^a\\ S{C}_{i,k}^a\\ f\left(S_{i,k}^a,C_{i,k+1}^f,S{C}_{i,k+1}^f\right)\end{array}\right)+\left(\begin{array}{c}{\delta }_{1,i,k}\\ {\delta }_{2,i,k}\\ {\epsilon }_{i,k}\end{array}\right)$ (8)

观测方程：

$\left(\begin{array}{c}{Q}_{i,k+1}\\ E{T}_{i,k+1}\end{array}\right)=\left(\begin{array}{c}h\left(S_{i,k+1}^f,C_{i,k+1}^f,S{C}_{i,k+1}^f\right)\\ h\left(C_{i,k+1}^f\right)\end{array}\right)+\left(\begin{array}{l}{\xi }_{1,i,k+1}\\ {\xi }_{2,i,k+1}\end{array}\right)$ (9)

2.3. 参数时变型式的确定

两参数月水量模型中的蒸散发参数C反映了与实际蒸散发计算过程相关的因素，C的大小主要受降水、气温、植被覆盖等因素的影响，可假定为降水、气温的线性函数；SC为流域最大蓄水能力，其大小主要受气候特征及植被覆盖的影响，可假定为降水、潜在蒸散发和气温的线性函数。

$\begin{array}{l}C=f\left(P,T\right)\\ SC=f\left(P,PET,T\right)\end{array}$ (10)

考虑到水文循环过程中的蒸发和产流不是瞬时响应过程，因此参数的变化与气候因子间可能存在滞后现象，即t时刻参数可能与t时刻前的气候因子有关。为确定时变参数的具体函数型式，可采用集合卡尔曼滤波算法先得到时变参数序列，再与降水、潜在蒸散发和气温等气候因子进行相关性分析。

当模型时变参数的影响因子确定后，以误差最小平方和最小为目标，采用SCE-UA优化算法率定线性函数的系数。

2.4. 评价指标

选用均方根误差RMSE、纳什效率系数NSE以及径流总量相对误差RE，作为径流模拟精度的评价指标。

$RMSE=\sqrt{\frac{1}{n}{\displaystyle {\sum }_{t=1}^n{\left(Q_{sim,t}-Q_{obs,t}\right)}^2}}$ (11)

$NSE=1-\frac{{\displaystyle \underset{t=1}{\overset{n}{\sum }}{\left(Q_{sim,t}-Q_{obs,t}\right)}^2}}{{\displaystyle \underset{t=1}{\overset{n}{\sum }}{\left(Q_{obs,t}-{\bar{Q}}_{obs}\right)}^2}}$ (12)

$RE=\frac{{\bar{Q}}_{sim}-{\bar{Q}}_{obs}}{{\bar{Q}}_{obs}}$ (13)

式中： $Q_{sim,t}$ 和 $Q_{obs,t}$ 分别为月径流模拟值和实测值， ${\bar{Q}}_{sim}$ 和 ${\bar{Q}}_{obs}$ 分别为模拟和实测月径流量的平均值。当RMSE、RE趋近于0，NSE趋近于1时，说明径流拟合的精度高。

3. 研究实例

3.1. 流域概况

选择美国东南部三个流域为研究对象，资料来源为MOPEX数据库。入选MOPEX数据库的流域均无大型水利工程，受人类活动影响较小 [12] 。三个流域的相对位置及流域情况分别由图1和表1给出，并根据干旱指数(AI)划分为干旱流域和湿润流域，AI为多年平均潜在蒸发值与多年平均降水的比值，该值大于等于1的流域为干旱流域，小于1的为湿润流域。本次研究使用的数据包括月降水、月潜在蒸发、月实际蒸散发、月径流和月平均气温，资料序列长度为1983~2003年。选取1983~1996年数据为水文模型率定期，1997~2003年数据为检验期。

3.2. 参数时变型式的确定

将集合卡尔曼滤波算法应用到研究区域，得到各流域的参数时变序列。对参数及气候因子进行相关性分析

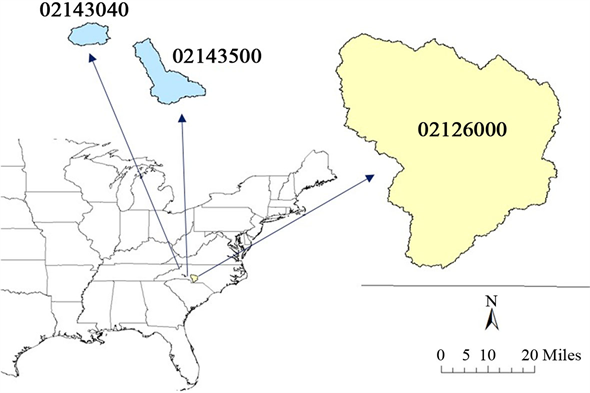
Figure 1. Location of the three study basins

图1. 研究流域地理位置

Table 1. Basic characteristics of the three basins

表1. 研究流域基本情况

的结果表明，参数C与降水间存在1个时段滞时，参数SC与降水和气温间存在3个时段滞时，且与同时段的潜在蒸散发及降水具有相关性。因此，可构建如下C和SC的时变型式：

$\begin{array}{l}C\left(t\right)={\alpha }_0+{\alpha }_{1}T\left(t\right)+{\alpha }_{2}P\left(t-1\right)\\ SC\left(t\right)={\beta }_0+{\beta }_{1}PET\left(t\right)+{\beta }_{2}P\left(t\right)+{\beta }_{3}P\left(t-3\right)+{\beta }_{4}T\left(t-3\right)\end{array}$ (14)

表2给出了参数的不同时变方案，包括参数均为常数、参数C和SC分别为时变参数以及两个参数均为时变参数四种方案。

3.3. 考虑参数为时变型式的径流模拟

表3给出了三个研究流域在不同模型参数方案下的径流模拟结果。由表可以看出，相较于常数参数，参数假定为时变型式的模拟效果在率定期和检验期均提高，其中将参数C和SC均考虑为时变型式的模拟效果最好。两个流域(02126000和02143040)检验期NSE值可达0.9，相较于常参数分别提高了18%和17%，率定期NSE值分别提高了17%和13%。由表还可以看出，参数值随流域不同呈现地区分布。相较于干旱流域，湿润流域的C值减小，SC值增大。

图2展示了检验期内流域02126000在两参数不变和时变情况下的月径流过程。由图可看出，采用两参数月水量平衡模型能较好地拟合出月径流量的变化过程，而双参数时变对洪峰的模拟效果更好。

3.4. 时变参数方案下降水变化对径流的影响

图3为三个研究流域1983~2003年逐年平均降水和径流系数，由图可看出，三个流域的降水和径流系数在1999~2001年都低于均值，2003年都达到最大值，且研究数据显示，气温变化在3%以内，潜在蒸散发的变化在

6%以内。因此，选取1999~2001三年为干旱年，2003年为湿润年来研究降水变化对径流的影响。表4给出了三个流域在所选干旱年和湿润年的降水径流变化情况，可以看出径流对降水的变化十分敏感，降水变化率60%~80%造成的径流变化率可达300%以上。

表5展示了双参数不变和时变方案对所选干旱年和湿润年的径流模拟结果。由RE(Q)值可知，在常数参数情况下，干旱年三个研究流域的径流总量相对误差均值为20%，湿润年为−17%，即在干旱年的模拟径流总量均大于实测值，湿润年均小于实测值。而采用双参数时变方案的径流总量估计均优于常数参数，干旱年和湿润年径流总量相对误差绝对值均值分别为10%和4.7%。由表5干旱年到湿润年的径流变化量 $\Delta {\bar{Q}}_{sim}$ 可知，相同降水变化下，时变参数方案的径流变化明显高于常参数方案。根据实测径流变化量计算得RE(ΔQ)值的结果显示，常数参数方案径流变化量相对误差均值为−30%，时变参数方案仅为7%，即常数参数方案很大程度低估相应径流变化量，而将参数考虑为时变型式能更准确地模拟降水变化时的径流变化，有利于气候变化下的径流预测及影响分析。

Table 2. The functional forms of time-varying scheme for two-parameter monthly water balance model

表2. 两参数月水量平衡模型参数时变型式方案

Table 3. Performance statistics for runoff estimates in the calibration and validation periods under different time-varying parameter schemes

表3. 研究流域不同时变参数方案率定期和检验期径流模拟结果

4. 结语

对变化环境下水文模型时变参数的函数型式构建以及不同参数方案对径流模拟的影响进行了探讨。选取美国MOPEX数据库的三个流域为研究区域，通过集合卡尔曼滤波算法估计模型参数序列，据此对参数和气候因

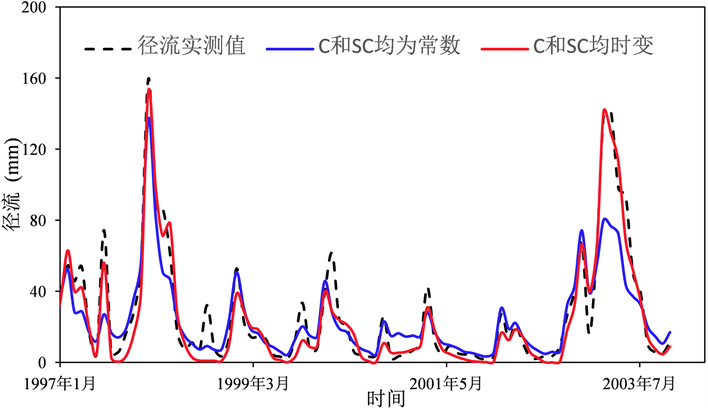
Figure 2. The runoff of observed (dashed line) and simulated (solid lines) for time-invariant (blue) and time-varying parameters (red) from 1997-2003 in catchment 02126000

图2. 流域02126000双参数不变和时变方案下1997~2003年实测径流与模拟径流过程图

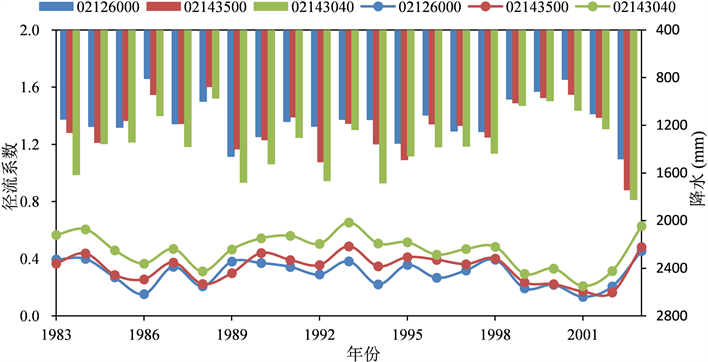
Figure 3. Annual mean precipitation and runoff coefficient in the three study basins

图3. 研究流域降水和径流系数逐年变化过程

Table 4. The observed precipitation and runoff during the dry years (1999-2001) and the wet year (2003) in the three study basins

表4. 研究流域干旱年(1999~2001)和湿润年(2003)降水径流实测数据变化情况

Table 5. The variation of simulated runoff in the dry years (1999-2001) and wet year (2003) under the constant and time-varying model parameters schemes

表5. 参数不变和时变方案下干旱年(1999~2001)和湿润年(2003)模拟径流变化情况

子进行相关性分析，并构建了参数与降水、潜在蒸散发和气温的函数型式。研究结论如下：

1) 将参数考虑为气候因子的函数型式能明显提高径流的模拟精度，率定期NSE可提高18%，检验期可提高17%，且峰值模拟更优，有利于准确的径流预报。

2) 径流对降水的变化非常敏感，以往气候变化研究中将参数视为常数会低估径流的变化，三个流域径流结果平均低估30%，而时变参数方案与实际情况更贴近，径流变化量误差降至7%。

本文只考虑了气候因子，未将人类活动的影响考虑在内；只采用了线性函数型式来反映参数与影响因子间的相关关系，未对时变参数的函数型式做讨论。这些问题有待后期研究。

基金项目

国家重点研发计划(2016YFC0400907)，湖北省自然科学基金(2017CFA015)，国家自然科学基金(51579180)资助项目。