1. 引言
光子晶体是一种介质折射率在空间中成周期性排列的人工功能材料 [1] [2] [3] ,最早由Yablonovitch [4] 和John [5] 各自独立提出,其周期(即晶格常数)与光波长的数量级大致相同 [6] 。按照光子晶体的折射率在空间中周期性变化的维度进行分类,它可以分为一维光子晶体、二维光子晶体和三维光子晶体 [7] 。目前,光子晶体的理论研究方法主要有平面波展开法 [8] 、有限时域差分法 [9] 和传输矩阵法 [10] 三种。
与半导体中的电子能带相类似,由于周期性势场的调制,光子晶体同样存在光子禁带(Photonic Band Gap, PBG) [11] [12] [13] ,频率处于禁带范围内的光波不能在光子晶体中传播,因此可以实现对光的调制。慢光 [14] [15] [16] 是指光波的波包群速度明显低于光在真空中传播的速度,可以通过耦合腔波导和线缺陷波导来实现 [17] [18] 。线缺陷波导中又分为后向散射和全反射两种散射机制 [1] 。光子晶体波导具有很多优异的性能 [19] ,可以实现大的时间延迟、增加相位移动的幅度、增强非线性效应 [20] [21] 等作用,在全光缓存、光学延迟线和全光开关等领域 [22] [23] 具有重要的应用。
本文利用扇面形散射元构建空气孔型六边形光子晶体结构,通过去掉一排散射元来构建线缺陷波导模型,计算不同散射元结构参数下对应的TM模式色散曲线,进而求其群折射率、群速度、归一化延迟带宽积、带宽和色散常数,比较分析不同波导结构的数据结果,寻找群折射率较大且带宽较宽的模型。
2. 模型结构
扇面形散射元的结构如图1所示,它具有三个结构参数:半径r、宽度d、角度
。三个自由度比普通的圆形和椭圆形散射元具有更高的可调性,因此更容易获得比较理想的结果。散射元的介电常数
(硅),填充介质的介电常数
(空气)。本研究采用六边形晶格结构,构建空气孔型光子晶体,图2为用扇面形散射元构建的光子晶体六边形晶格结构。
3. 模拟分析
3.1. 慢光中的基本概念
众所周知,群折射率ng可以由公式(1)表示:

Figure 2. Photonic crystal with hexagonal lattice structure
图2. 光子晶体六边形晶格结构
(1)
其中ω是入射波(脉冲)的中心角频率,
,neff是有效折射率,λ是工作频率的波长。带入k对公式(1)进一步展开得到公式(2):
(2)
对慢光而言,通常
,则公式(3)近似为:
(3)
简化得公式(4):
(4)
公式(4)中,ngΔω/ω称为延迟带宽积,是评价慢光的主要参数。有效折射率的最大变化可表示为公式(5):
(5)
公式(5)中,
和
指的是群折射率
取±x%时对应的频率上下限,一般取±10%,a值也是根据工作波长而作相应改变后的数值。色散系数D则有公式(6)表示。
(6)
目前,归一化延迟带宽积已成为评价慢光效应的主要参数,因为它既包含了群折射率的大小,又包含了带宽的宽度。而研究发现,群折射率越大,对应的带宽会越小,具体采用哪种参数的模型,应视具体情况而定。
3.2. 色散曲线的规律分析
在图2完整的六边形光子晶体晶格结构中,引入线缺陷,构成面对面型线缺陷波导结构,面对面指的是散射元的相对位置,如图3所示。
利用平面波展开法,改变散射元的角度
,在第一布里渊区范围(位于0.3~0.5)内,寻找归一化频率
随
的变化关系,如图4所示。可以发现,随着
的增大,色散曲线由向下凹逐渐向向上凸转变,在转变的过程中,就会出现一段线性区域,根据公式(3),具有线性区域的色散曲线容易找到平坦的慢光,因此寻找理想慢光也就是寻找存在线性区域的色散曲线。
3.3. 面对面型线缺陷波导的慢光特性分析
由课题组以前的研究得知 [14] [15] [16] ,空气孔型晶格结构的TM模式比较容易产生较理想的慢光,因此本研究针对这一模型展开研究,目的在于寻找群折射率较大且带宽较宽的模型,增大归一化延迟带
宽积(
)。
采用控制变量法,通过微调散射元参数进行优化,找到比较平坦的群折射率曲线,如图5所示。图5中对应的模型分别为: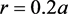 ,
,
,
;
,
,
,
;
,
,
,
;
,
,
,
;
,
,
,
,这是最大的群折射率值,同时也对应着最小的群速度,
。归一化延迟带宽积的最大值为0.213。表1中的带宽是在工作波长
下计算出的,变化范围为2.1~8.5 nm,对应的晶格常数
。若用1 Thz的工作频率,即
,可获得398.7~1641.2 nm
,
,
,
;
,
,
,
;
,
,
,
;
,
,
,
;
,
,
,
,这是最大的群折射率值,同时也对应着最小的群速度,
。归一化延迟带宽积的最大值为0.213。表1中的带宽是在工作波长
下计算出的,变化范围为2.1~8.5 nm,对应的晶格常数
。若用1 Thz的工作频率,即
,可获得398.7~1641.2 nm

Figure 3. Face-to-face line defect waveguide structure
图3. 面对面型线缺陷波导结构
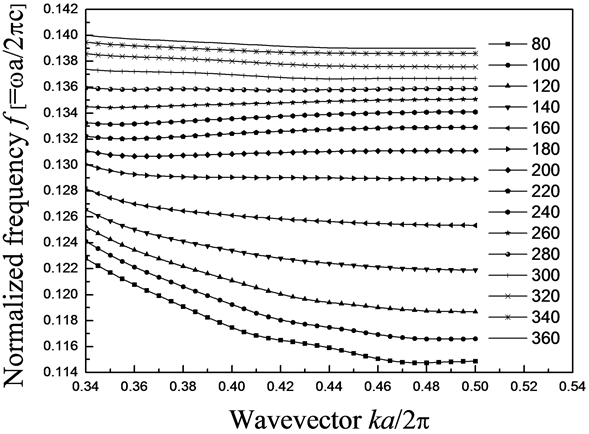
Figure 4. Relationship of dispersion curve with θ
图4. 色散曲线随θ的变化关系

Figure 5. Group refractive index curve of face to face line defect waveguides
图5. 面对面型线缺陷波导的群折射率曲线

Table 1. n g , Δ λ , n g Δ ω / ω , v g in face-to-face line defect waveguide
表1. 面对面型线缺陷波导的
范围的平带带宽,对应的晶格常数为35.86 μm。
根据3.1中给出的公式,计算其各自的群速度、归一化延迟带宽积和带宽,见表1。其中Δλ的误差是±10%,单位是nm。
根据式(6),取
,使
保持在±10%的变化范围内,计算各个模型的色散常数D,如图6所示。
D的单位是ps/mm∙nm,计算当
时,波长的变化范围,即带宽,如表2所示,其最大值可达3.1 nm。若令
,带宽可达1641.2 nm。
3.4. 背对背型线缺陷波导的慢光特性分析
将图3中的散射元全部旋转180˚,得到背对背型线缺陷波导结构,见图7。
研究方法同3.3,计算其群折射率,寻找比较理想的慢光模型,如图8所示。各个模型的参数与面对面型的基本一致,只是个别角度有细微的变化。
时,
,为最大值。群折射率可以实现39.0~92.6的可调范围。
表3为
时,各个参数模型所对应的群折射率、带宽、归一化延迟带宽积和群速度,此时晶格常数
。

Table 2. a and Δ λ for | D | ≤ 1 in face to face line defect waveguides
表2. 面对面型线缺陷波导
时的a及
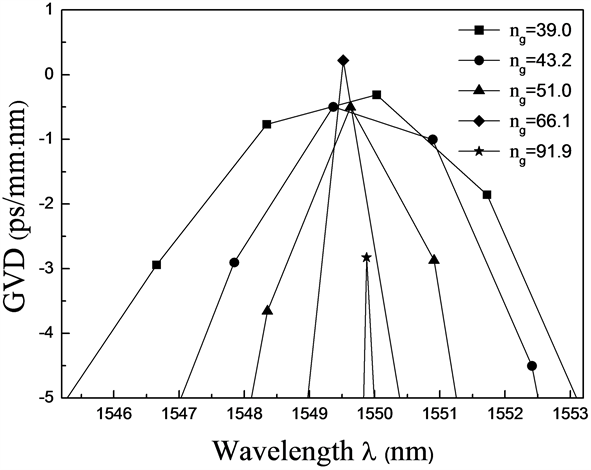
Figure 6. GVD curves of face to face line defect waveguides
图6. 面对面型线缺陷波导的GVD曲线

Figure 7. Back-to-back line defect waveguide
图7. 背对背型线缺陷波导

Figure 8. Group refractive index curve of back-to-back linear defect waveguides
图8. 背对背型线缺陷波导的群折射率曲线

Table 3. n g , Δ λ , n g Δ ω / ω , v g in back-to-back face line defect waveguides
表3. 背对背型线缺陷波导的
由表3可知,带宽的变化范围为8.5 nm,最大归一化延迟带宽积为0.215。若取
,即 ,平带带宽可实现397.2~1649.6 nm的变化范围,晶格常数为35.862 μm。
,平带带宽可实现397.2~1649.6 nm的变化范围,晶格常数为35.862 μm。
取
,
,计算其色散常数D,如图9所示。由表中数据得,
时,最大带宽可达2.73 nm。取
,最大带宽可达1649.6 nm。
同样的,
的带宽值可由表4表示,D的单位还是ps/mm∙nm。
3.5. 旋转30˚后线缺陷波导的慢光特性分析
将图3中的扇面形散射元对称旋转30˚,得到旋转30˚线缺陷波导,如图10所示。
利用控制变量法,寻找比较理想的群折射率曲线,如图11所示。对应的参数分别为:
,
,
,
;
,
,
,
;
,
,
,
;
,
,
,
;
,
,
,
,为最大值。即通过调控参数,此模型可以实现群折射率从36.2到83.3的调谐。
表5列出了工作波长 时,各个参数模型的群折射率、带宽、归一化延迟带宽积和群速度,此时晶格常数
。
时,各个参数模型的群折射率、带宽、归一化延迟带宽积和群速度,此时晶格常数
。
由表5可以看出,平带带宽可实现3.0~10.8 nm的调谐,最大归一化延迟带宽积为0.253,最小的群速度为0.012c。若令工作频率
,平带带宽可实现583.2~2094.3 nm的变化。图12为

Figure 9. GVD curve of a back-to-back line defect waveguide
图9. 背对背型线缺陷波导的GVD曲线

Table 4. a and Δ λ for | D | ≤ 1 in back-to-back line defect waveguides
表4. 背对背型线缺陷波导
时的a及

Figure 10. Rotating 30˚ post-line defective waveguide
图10. 旋转30度线缺陷波导

Figure 11. The group refractive index curve of a linear defect waveguide after rotation 30˚
图11. 旋转30˚后线缺陷波导的群折射率曲线

Table 5. n g , Δ λ , n g Δ ω / ω , v g in a linear defect waveguide after rotation 30˚
表5. 旋转30˚后线缺陷波导的
时,散射元旋转30˚后线缺陷波导的色散常数曲线。
表6为
,
时的a值及带宽值。可见,带宽的最大值可达4.3 nm。若令
,

Figure 12. GVD curve of the waveguide with line defects after rotation 30˚
图12. 旋转30˚后线缺陷波导的GVD曲线

Table 6. a and Δ λ in a linear defect waveguide after rotation 30˚ when | D | ≤ 1
表6. 旋转30˚后线缺陷波导
时的a及
则带宽最大可达2094.3 nm。
3.6. 三种模型的比较分析
对于面对面型和背对背型线缺陷波导结构,比较表1和表3可知,无论是群折射率和带宽,还是归一化延迟带宽积和群速度,这两种模型的数据结果几乎完全相同,只有很细微的差别,可以认为无差别。比较表2和表4,可以看出,
时,两种模型的带宽值有一定的差别,并且无明显的大小关系。比如, 时,面对面线缺陷型波导结构的带宽值为3.1 nm,背对背型线缺陷波导结构的带宽值为2.73 nm,前者大于后者。而当
时,面对面型波导的带宽值为2.1 nm,背对背型波导的带宽值为2.26 nm,前者小于后者。当
时,面对面型波导的带宽值为0.3 nm,但背对背型波导在
时却无带宽。当
时,面对面型波导无带宽值,而背对背型在
时的带宽值为0.62 nm。
时,面对面线缺陷型波导结构的带宽值为3.1 nm,背对背型线缺陷波导结构的带宽值为2.73 nm,前者大于后者。而当
时,面对面型波导的带宽值为2.1 nm,背对背型波导的带宽值为2.26 nm,前者小于后者。当
时,面对面型波导的带宽值为0.3 nm,但背对背型波导在
时却无带宽。当
时,面对面型波导无带宽值,而背对背型在
时的带宽值为0.62 nm。
对于面对面型和旋转30˚后线缺陷波导结构,比较表1和表5可知,对于群折射率,旋转30˚后波导结构的数值均比面对面型的要小,因此群速度值均比面对面型波导结构的大。同时,旋转30˚后的带宽值均比面对面型的要大。而对于归一化延迟带宽积,却没有明确的大小关系。比如,
时的带宽积,面对面型要小于旋转30˚后的;但
时的带宽值,面对面型的要大于散射元旋转30˚后的波导结构。对于
时的带宽值,面对面型波导结构明显小于旋转30˚后的波导结构。
4. 结论
本文用扇面形散射元构建六边形空气孔型光子晶体线缺陷波导结构,利用控制变量法,调节散射元的结构参数,分别计算其TM模式下的色散曲线,进而得到其群折射率、群速度、带宽、归一化延迟带宽积和色散常数。分别对面对面型、背对背型和旋转30˚后的线缺陷波导结构进行计算,经过比较分析可以得到:通过优化,采用面对面型或背对背型模型,都可以实现较好的慢光效果,优化结构的归一化延迟带宽积分别为0.213,0.215,只是结构参数不同;旋转30˚后的模型,可以很好实现波导的慢光平带带宽值变大,优化结构的归一化延迟带宽积为0.253,也有明显提高,但对于较高的群折射率这一优势不明显。在具体的研究中,可以视具体需要选择结构模型、参数等,通过优化设计,获得较理想的慢光效果。
基金项目
本文国家自然科学基金(11144007)和山东省自然科学基金(ZR2016AM27)资助课题。