Abstract:
其中
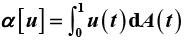
,
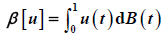
;A,B为有界变差函数;
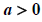
,
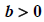
;非线性项
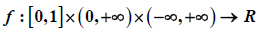
是连续的,它依赖于导数
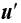
并且是可变号的。本文根据不动点指数理论,讨论得到对于上述问题的多个正解的存在性结果。
In this paper, we consider the singular semi-positive non-local boundary value problem
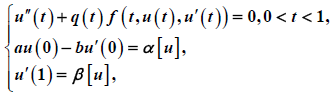
where
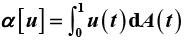
,
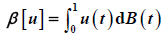
; A and B are bounded variation functions;
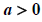
,
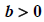
; the nonlinear item
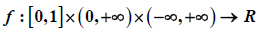
is continuous and it is allowed to change the sign. Based on the fixed point index theory, this paper studies the existence of multiple positive solutions to the above problem.
1. 引言
在本文中,我们考虑右端函数带导数项的奇异半正非局部边值问题
(1)
其中边值条件(BCs)是关于线性泛函的,并且由Riemann-Stieltjes积分给出:
并且A,B为有界变差函数;
,
;非线性项
是连续的,它依赖于导数
并且是允许变号的。
2006年,G.C.Yang在文献 [1] 中讨论了奇异的Dirichlet边值问题
在假设
(H1)
,
(H2)
,
(H3)
,
(H4)对任意
,且
,有
,
(H5)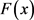 在
在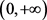 上单调递减下,文章运用了Schauder不动点定理得到上述问题的正解的存在性。
上单调递减下,文章运用了Schauder不动点定理得到上述问题的正解的存在性。
2009年,Gennaro Infante在文献 [2] 中考虑了奇异非局部边值问题
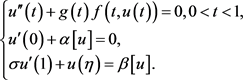
假设:
(i) g为非负的 函数,
函数,
(ii) f是非负的函数,且在第二个变量处是有奇异性的,
(iii)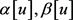 是
是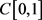 上的有界线性泛函,并且
上的有界线性泛函,并且
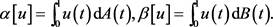
通过补充定义,将f的定义域扩大为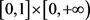 ,也就是定义
,也就是定义
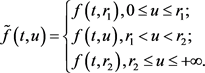
考虑算子
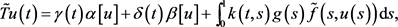
通过寻找算子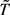 在
在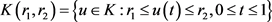 中的不动点来得到边值问题的正解。
中的不动点来得到边值问题的正解。
2011年,C. Ji,D. O’Regan,B.Yan等人在文献 [3] 中考虑了二阶奇异三点边值问题

其中 是变号函数,并且在
是变号函数,并且在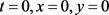 处可能是具有奇异性的。运用不动点指数理论,讨论并得到了正解的存在性以及不存在性。
处可能是具有奇异性的。运用不动点指数理论,讨论并得到了正解的存在性以及不存在性。
2014年,B.Yan,O'Regan等人在文献 [4] 中讨论了非线性非局部边值问题
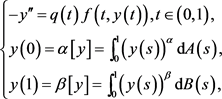
其中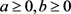 。通过不动点指数和混合单调方法,得到带非线性积分边值条件的奇异非局部边值问题的多个正解的存在和唯一性结果,这里的非线性项f可能是奇异的并且可以变号。
。通过不动点指数和混合单调方法,得到带非线性积分边值条件的奇异非局部边值问题的多个正解的存在和唯一性结果,这里的非线性项f可能是奇异的并且可以变号。
2014年,Zima在文献 [5] 中考虑了

作者假设:(i)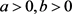 ,(ii) f在
,(ii) f在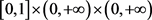 上连续且非负的,考虑f在空间变量的0值处有奇异性,也就是f可能在第二个变量
上连续且非负的,考虑f在空间变量的0值处有奇异性,也就是f可能在第二个变量 和第三个变量
和第三个变量 处有奇异性。边值条件(BCs)由Riemann-Stieltjes积分给出:
处有奇异性。边值条件(BCs)由Riemann-Stieltjes积分给出:
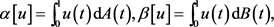
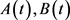 是有界变差函数,并且
是有界变差函数,并且 。Zima通过限制奇异非线性项f在
。Zima通过限制奇异非线性项f在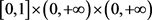 的一个合适的子集
的一个合适的子集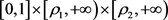 上,利用Krasnoselskii-Guo锥拉压不动点定理,建立了上面问题的正解存在的充分性条件。
上,利用Krasnoselskii-Guo锥拉压不动点定理,建立了上面问题的正解存在的充分性条件。
2. 预备知识及引理
令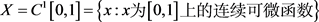 ,对于
,对于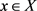 ,我们定义
,我们定义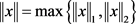 ,其中
,其中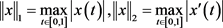 ,则
,则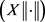 是一个Banach空间。
是一个Banach空间。
定义

显然P是X中的一个锥。
我们主要考虑以下的情况:
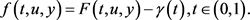
为了叙述的方便,我们给出如下的假设:
(C1)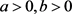 ,
,
(C2) 是连续的函数,
是连续的函数,
(C3) 是有界的变差函数,并且
是有界的变差函数,并且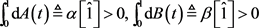 ,
,
(C4)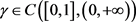 ,
,
(C5)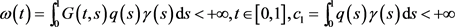 ,
,
(C6)存在 上的连续函数
上的连续函数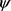 ,并且在
,并且在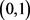 上
上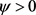 ,使得当
,使得当
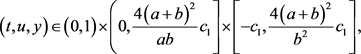
有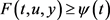 ,并且
,并且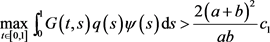 。
。
对于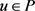 ,我们定义:
,我们定义:
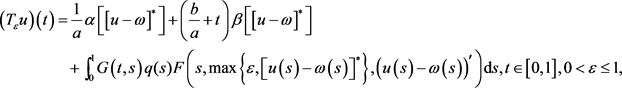
其中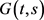 为以下问题的Green函数:
为以下问题的Green函数:
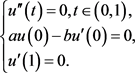
即
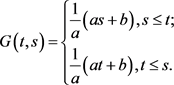
此外,
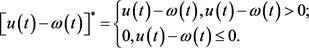
我们定义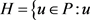 满足
满足 ,
,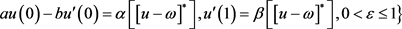 。
。
引理2.1:对于任意的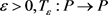 为一个全连续的算子。
为一个全连续的算子。
证:首先,我们来证明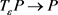 。
。
对于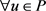 ,有
,有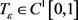 ,并且
,并且
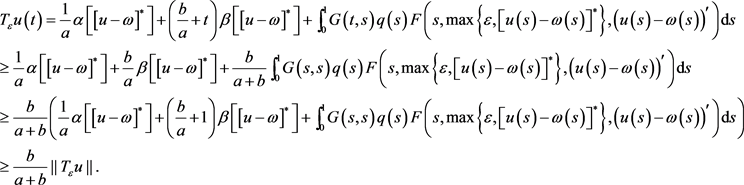
又因为
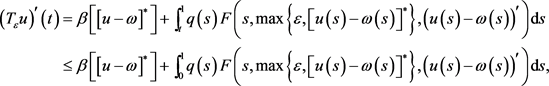
所以
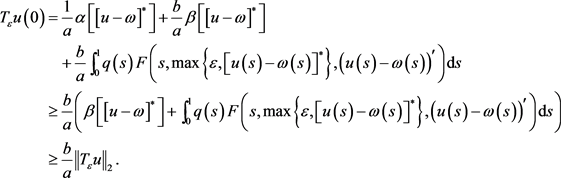
因此, 。
。
又根据F具有连续性,利用Ascoli-Arzela定理,可以得到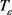 是全连续的算子。
是全连续的算子。
引理2.2:假设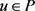 ,那么
,那么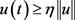 ,
,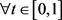 ,其中
,其中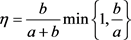 。
。
证:因为
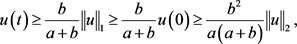
所以,
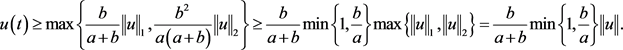
引理2.3:假设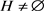 ,(C6)成立,那么存在,使得对于
,(C6)成立,那么存在,使得对于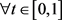 ,
,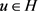 ,有
,有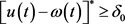 。
。
证:我们令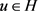 ,则得到以下的两种情形:
,则得到以下的两种情形:
(i)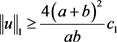 。
。
因为 ,所以
,所以
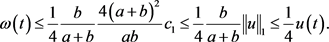
因此,有
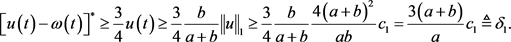
(ii)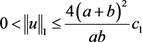 。
。
通过计算能够得出

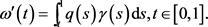
所以,
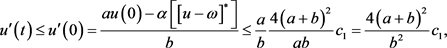
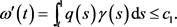
因此
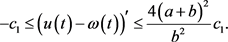
根据假设(C6),我们知道这里存在一个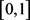 上的连续函数
上的连续函数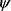 ,使得
,使得
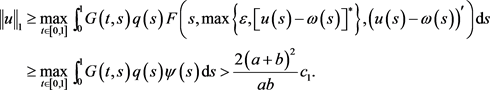
又由于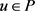 ,
,
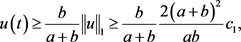
但
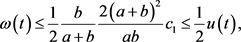
因此

令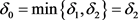 ,则对
,则对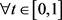 ,
, 有
有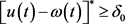 。
。
引理2.4: [6] 设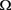 为实Banach空间E中的一个有界开集,P为E中的一个锥,
为实Banach空间E中的一个有界开集,P为E中的一个锥,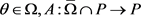 为连续紧算子,假设
为连续紧算子,假设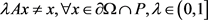 ,则
,则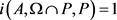 .
.
引理2.5: [6] 设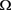 为实Banach空间E中的一个有界开集,P为E中的一个锥,
为实Banach空间E中的一个有界开集,P为E中的一个锥,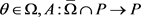 为连续紧算子,假设
为连续紧算子,假设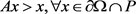 ,则
,则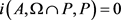 .
.
引理2.6:假设存在一个函数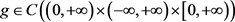 ,使得对于
,使得对于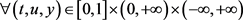 ,有
,有
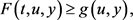 (2)
(2)
并且函数g满足
 (3)
(3)
对于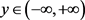 是一致成立的,则存在
是一致成立的,则存在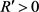 ,使得对于
,使得对于 ,有
,有
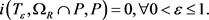
证:根据(3),我们可以知道存在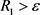 ,使得
,使得
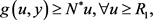
其中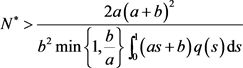 .
.
再根据(2),有
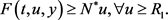 (4)
(4)
设 .
.
下面证明
 (5)
(5)
若不然,我们假设存在一个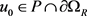 ,即
,即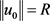 ,使得
,使得 。
。
根据引理3.2,有
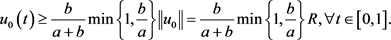
因为
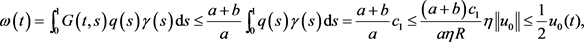
所以有
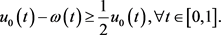
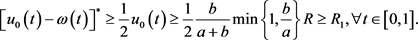
再由(4)式可知,

因此,有

矛盾。因此(5)式成立。
根据引理2.5我们能够知道 。
。
3. 主要结果
定理3.1:假设(C1)~(C6)成立,且满足以下的条件
(A1)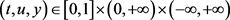 ,有
,有
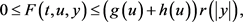 (6)
(6)
其中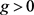 在
在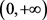 上是连续的并且单调不增的,
上是连续的并且单调不增的,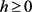 在
在 上是连续的,
上是连续的,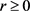 在
在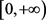 上是连续的且单调不减的,
上是连续的且单调不减的,
(A2)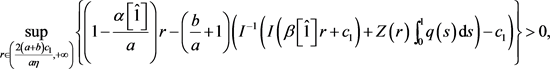 (7)
(7)
其中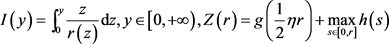 ,则边值问题(1)至少存在一个正解。
,则边值问题(1)至少存在一个正解。
证:因为(7),我们可以令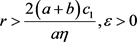 ,使得
,使得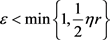 ,
,
 (8)
(8)
我们令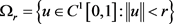 。
。
下面我们就来证明
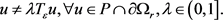 (9)
(9)
若不然,我们假设存在一个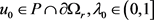 ,使得
,使得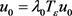 。
。
因为
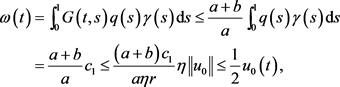
所以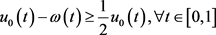 。
。
又根据引理2.2,有
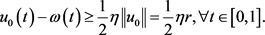
因为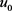 满足
满足
 (10)
(10)
所以能够得到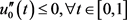 ,又由于
,又由于 ,从而有
,从而有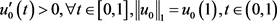 ,易证
,易证
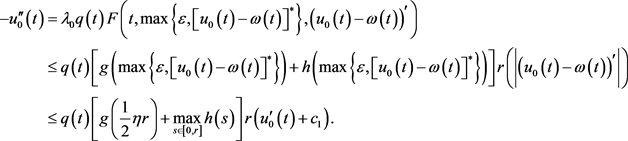
因此
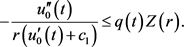 (11)
(11)
对上式从t到1做积分,能够得到
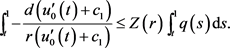
即
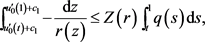
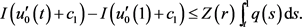
再结合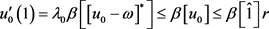 ,得
,得
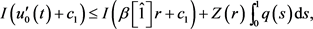
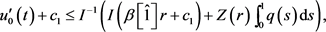
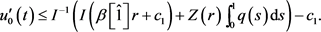 (12)
(12)
令 得
得
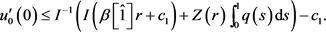
结合(10),有
 (13)
(13)
对(12)从0到1做积分,有

于是,根据(13),得到
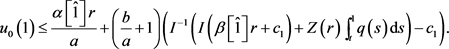
因此
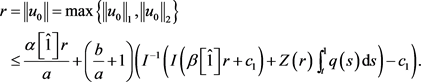
这与(8)式矛盾。因此(9)成立。根据引理2.4,有
 (14)
(14)
所以,存在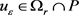 ,使得
,使得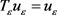 。所以引理2.3中的
。所以引理2.3中的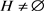 ,即存在一个
,即存在一个 ,使得
,使得
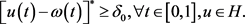 (15)
(15)
假设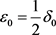 ,且
,且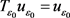 。显然,
。显然,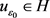 ,根据
,根据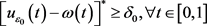 和
和
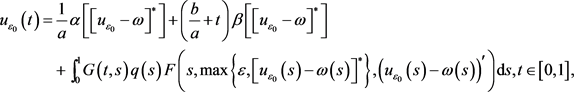
能够得到

假设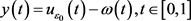 ,经验证能够得到
,经验证能够得到
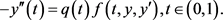
因为

所以根据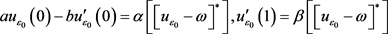 ,可知
,可知
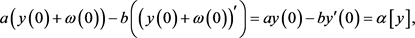

因此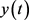 是边值问题(1)的一个正解。
是边值问题(1)的一个正解。
定理3.2:假设定理3.1的条件和引理2.6的条件同时成立,那么边值问题(1)至少存在两个正解。
证:我们取(8)中的r,令 ,
,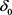 的定义同引理2.3,取引理2.4中
的定义同引理2.3,取引理2.4中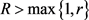 。设
。设
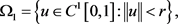
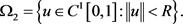
根据引理2.6和定理3.1,有
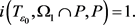
并且

所以
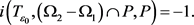
因此存在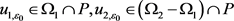 ,使得
,使得
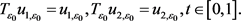
假设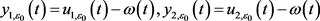 。易得,
。易得,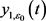 和
和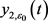 为边值问题(1)的两个正解。
为边值问题(1)的两个正解。
基金项目
山东省自然科学基金(ZR2018MA022)资助。
参考文献