1. 引言
本文考虑如下非线性非局部边值问题
(1.1)
其中边值条件(BCs)是关于线性泛函,且由Riemann-Stieltjes积分给出:
2000年,Guidotti和Merino在文献 [1] 中研究了
该方程代表了一个在稳定状态下的长度为1的加热棒模型。它在 时是绝缘的,加热或冷却操作是在
处的控制器根据传感器所反馈回的 t=0 时的温度来进行的。
时是绝缘的,加热或冷却操作是在
处的控制器根据传感器所反馈回的 t=0 时的温度来进行的。
2006年,Webb和Infante在文献 [2] 中研究了以下方程正解的存在性问题:
该方程也是一个具有稳定解的加热棒模型,不同的是,温度变化是由
处控制器通过任意点 t =η 处传感器温度变化情况反馈控制的,而不是
处。该文根据不动点指数理论,讨论了随参数的变化多个非平凡解的存在性情况。
2012年,Webb在文献 [3] 中研究了温控器模型正解的存在性:
其中,
。这是一类更为一般的边值条件,传感器为线性泛函。由于此时的传感器覆盖了加热棒的某一些点或某一连续区间,所以更符合实际。该文通过研究其格林函数的性质,讨论了以上问题何时存在多个正解以及何时不存在正解。
2015年,Infante在文献 [4] 中研究了Neumann型非局部边值问题
该文通过研究摄动Hammerstein积分方程
利用不动点指数理论,得到以上问题存在多个非平凡解。
本文在第二节,给出了相关的预备知识和引理。在第三节,我们分别通过利用两个锥上的不动点定理和Leggett-Williams三解定理得到了方程两个正解和三个正解的存在性结果。
2. 预备知识和引理
本文中,我们作如下假设:
(H1)
;
(H2)
;
(H3)
是有界变差函数,且
。
对于问题(1.1),我们将其转化为对以下相应Hammerstein积分方程解的存在性:
其中
为以下问题的Green函数:
即
则
且
令
。对
,定义
则
为一Banach空间。
,
考虑
显然,
为X中的两个锥,且
。对
,定义
令
,我们定义算子
如下:
使
注1:若
为一泛函,  ,则
。
,则
。
引理2.1:
为全连续算子。
证明:首先我们证明
。
对
,有
,且
所以,
。
再由f的连续性及
的定义,通过Arzela-Ascoli定理,我们知 为全连续算子。
为全连续算子。
引理2.2:函数
是三点边值问题(1.1)的正解,当且仅当
是算子A在锥中的不动点。
引理2.3:如果算子
是全连续的,那么算子
是全连续的。
注2:根据f的连续性,
是全连续的,因此由引理2.2知,算
也是全连续的。
引理2.4:如果u是T的不动点,那么u也是A的不动点。
证明:假设u是T的不动点,则对
,
,u也是A的不动点。
为此,我们只需要证如果
,那么
反之,如果
,使得 。令
为包含
点且使得
。令
为包含
点且使得  的最大区间,则
,从而
的最大区间,则
,从而
1)
。
若
,则
,且
,而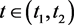 时,
,即
在
上为凹函数,所以
。但又
时,
,即
在
上为凹函数,所以
。但又
可知
由此得出矛盾。
若
,此时  ,且
,且  ,故
,故
由此也得出矛盾。
2)
。
若
,则
,且
于是  ,
,
。
所以,
矛盾。
若
,则
,于是
从而
单调递减,而我们知
,从而
。这与
矛盾。
引理2.5 [5] (Leggett-Williams三解定理):设  是全连续的, a 是P上的一个非负连续凹泛函,满足当
时,
,假设存在
,使得
是全连续的, a 是P上的一个非负连续凹泛函,满足当
时,
,假设存在
,使得
(C1) 当
,且
时,恒有
;
(C2) 当
时,恒有
;
(C3) 当
且
时,恒有
,
则A至少有三个不动点
,满足:
引理2.6 [6] :令X为一实Banach空间,其上的范数为
,
为两个锥,且
。假设
为两个全连续算子,且
为一连续泛函,满足对任意
,有
,其中
是一个常数。若存在常数
,使得
(M1)
;
(M2)
,且
;
(M3)
,
则T在K中至少有两个不动点
,满足
3. 主要结果
定理3.1:假设条件(H1)、(H2)、(H3)成立,又设存在正数
满足
,且使得f满足如下假设:
(H4)
;
(H5)
;
(H6)
;
(H7)
;
(H8)
;
(H9)
,
则边值问题(1.1)至少存在两个正解
满足
证明:对任意
,
由假设(H5)、(H7)有
故引理2.6中条件(M1)满足。
对任意
,即
,由假设(H5)、(H7)有
对
,即
,且
,我们有
所以
而
即
由假设(H6)、(H8)有
从而
。
另一方面,由引理2.1知,
故
引理2.6中条件(M2)满足。
最后,我们证明定理中的条件(M3)满足。
对
,即
,且
。
另一方面,
故
得
所以
由假设(H9)知,
通过假设(H4),我们有
从而
综上,引理2.6中的条件全部满足,则T有两个不动点
满足
再由引理2.4知,
为A的不动点,从而边值问题(1.1)至少存在两个正解。证毕。
定理3.2:假设(H1)~(H4)成立,又设
(
) 存在正数
满足
,使得
(
)
;
(
)
;
(
)
;
(
)
,
则边值问题(1.1)至少存在三个正解。
证明:定义非负连续凹泛函
,
显然,任取
,
。
又若
,有
且
。由假设(
)、(
)有
故
下面验证引理2.5中的条件(C1)~(C3)。
1) 取
, t∈[0.1],
故
且任取
,即
所以,由假设(
)、(
)有
所以,引理中的条件(C1)满足。
2) 对 ,由假设(
)、(
)有
,由假设(
)、(
)有

所以,引理中的条件(C2)满足。
3) 取
,且
,则
所以,引理中的条件(C3)满足。
由Leggett-Williams三解定理,T至少有三个不动点
,且满足
再由引理2.4知,
为A的不动点,从而边值问题(1.1)至少存在三个正解。证毕。