基于浸入边界–格子Boltzmann方法模拟动边界绕流问题

Simulation of the Flow around a Moving Boundary Based on the Immersed Boundary Combined Lattice Boltzmann Method

摘要: 组合浸入边界和格子Boltzmann方法(IB-LBM)实现对复杂动边界问题的数值模拟。通过格子Boltzmann方法快速计算流场分布(采用D2Q9离散速度模型)，通过隐式直接力浸入边界法处理流场边界问题。借助求解不可压缩N-S方程组的分步投影方法的思想，在时间上推进求解基于浸入边界法的耦合系统方程，从而实现对复杂动边界流动问题快速有效的求解。以雷诺数为100的圆柱绕流为基准算例，分别计算圆柱在不同旋转角速度下的升、阻力曲线和流场分布特性，并与其他文献的计算结果对比，验证了IB-LBM计算动边界流动问题的有效性。

Abstract: The main content of this paper is to use the immersed boundary combined lattice Boltzmann me-thod (IB-LBM) to simulate the moving boundary problem. By Lattice Boltzmann method, the flow field is simulated using D2Q9 model, and the movement boundary is treated by the implicit direct force method of the immersed boundary method, which is solved using the projection step method. Finally, a flow around a rotating cylinder with Reynolds number of 100 at different angular velocity as a benchmark example has been simulated, and the lift and drag coefficient as well as flow field distribution has been investigated and compared with the results of other literature. It is also verified that the immersed boundary combined lattice Boltzmann method is valid and robust to simulate movement boundary flowing problems.

1. 引言

绕流是常见的物理现象，也是经典的力学问题。例如圆柱绕流，在一定流动工况下会在结构物后发生漩涡脱落现象。当圆柱以一定角速度主动旋转时，漩涡脱落的位置又会发生复杂的变化。尽管求解复杂动边界问题的数值方法近年来得到快速的发展，但要准确并快速的求解复杂动边界的绕流问题仍然是一个具有挑战性的难题。格子Boltzmann方法是近年来出现的计算流体力学的新方法，具有程序易实施、计算速度快、良好的并行特性等优点 [1] 。此外，为了扩展格子Boltzmann方法的应用范围，近几年来，格子Boltzmann方法得到快速的发展，如文献 [2] 提出了基于泰勒级数展开和最小二乘的格子Boltzmann方法(TLLBM)。同时浸入边界法在模拟心脏瓣膜运动，昆虫以及鱼类游动等一系列动边界流动方面取得了重大的成功。自浸入边界法提出至今，科研工作者们对其进行了大量的改进，研究出各种基于浸入边界法的数值方法。如Goldstein，等 [3] 提出了虚拟边界法(Virtual Boundary Method)模型，适用于复杂的几何体周围流场的模拟。文献 [4] 建立了一种基于浸入边界法的投影法，用于模拟流体一刚体作用时的数值计算。文献 [5] 阐述了自适应加密网格的生成方法、生成过程以及数据结构和网格关系。加密判断标准、边界条件以及在这种网格下的迭代计算过程。文献 [6] 对运动边界问题、浸入边界法和非定常不可压缩流动的直接数值模拟算法进行研究，编写CFD程序。并在此基础上获得更高精度，改进原先算法的缺陷和不足，使得浸入边界法应用到运动边界问题上。同时，组合浸入边界和格子Boltzmann方法(IB-LBM)实现对复杂动边界问题的数值模拟也引起大家的广泛关注，如文献 [7] 提出了基于速度修正的浸入边界-格子Boltzmann方法，同时将该方法扩展至三维来进行三维流场的数值模拟。文献 [8] 利用IB-LBM方法对泊萧叶流中血红细胞的运动进行模拟。文献 [9] 提出了一种基于非均匀四叉树网格下的IB-LBM，通过引入边界处理技术和大涡模型，实现了较大雷诺数下圆柱绕流的模拟。文献 [10] 提出了一种稳定的IB-LBM，该方法在保证边界条件精确满足的同时，还能够准确地模拟中高雷诺数下的物体绕流问题。为此，本文将一种隐式直接力方法与格子Boltzmann方法有效结合，实现动边界流动问题的快速准确求解。

2. 物理数学模型和数值方法

2.1. 物理数学模型

浸入边界法组合格子Boltzmann方法的流动控制方程可表示为

$f_{\alpha }\left(x+e_{\alpha }\delta t,t+\delta t\right)-f_{\alpha }\left(x,t\right)=-\frac{1}{{\tau }_{LB}}\left[f_{\alpha }\left(x,t\right)-f_{\alpha }^{eq}\left(x,t\right)\right]+\delta t{F}_{\alpha }\left(x,t\right)$ (1)

$f_{\alpha }^{eq}=\rho {\omega }_{\alpha }\left[1+\frac{e_{\alpha }\cdot u}{c_s^2}+\frac{{\left(e_{\alpha }\cdot u\right)}^2}{2c_s^4}-\frac{u^2}{2c_s^2}\right]$ (2)

$F_{\alpha }\left(x,t\right)\text{=}\left(1-\frac{1}{2{\tau }_{LB}}\right){\omega }_{\alpha }\left[\frac{e_{\alpha }-u}{c_s{}^2}+\frac{e_{\alpha }\cdot u}{c_s{}^4}{e}_{\alpha }\right]\cdot f$ (3)

其中， $f_{\alpha }$ 为速度分布函数， $x$ 为空间位置矢量， $e_{\alpha }$ 为离散速度， $\delta t$ 为时间步长， $f_{\alpha }^{eq}$ 为平衡态分布函数，

${\tau }_{LB}=0.5+\frac{\nu }{c_s{}^2\delta t}$ 为无量纲松弛时间， $c_s\text{=}\frac{\Delta x}{\sqrt{3}\delta t}$ 为格子声速， $\Delta x$ 为格子网格步长， $\nu$ 为流体运动黏性系数，

${\omega }_{\alpha }$ 为权系数， $F_{\alpha }\left(x,t\right)$ 为外力。 $f$ 表示虚拟的力源项，这里指固体边界存在对流体产生的作用力密度，可表示为：

$f\left(x,t\right)={\displaystyle \underset{\Gamma }{\int }F\left(X\left(s\right),t\right)}\delta \left(x-X\left(s,t\right)\right)\text{d}s$ (4)

式中， $X$ 和 $F$ 分别表示拉格朗日坐标和浸入固体边界力密度， $\delta \left(x-X\left(s,t\right)\right)$ 为近似的光滑函数。

本文采用D2Q9模型 [11] ，见图1，该模型是二维模型，且有9个速度方向，分别为原点1个、正方形的水平轴和竖直轴方向各2个并且对称分布，对角线方向有4个，也是对称分布，其速度配置可表示为：

$e_{\alpha }=\{\begin{array}{l}\left(0,0\right)\alpha =0\hfill \\ c\left(\cos [\left(\alpha -1\right)\frac{\text{π}}{2}],\sin \left[\left(\alpha -1\right)\frac{\text{π}}{2}\right]\right)\alpha =1,2,3,4\hfill \\ \sqrt{2}c\left(\cos \left[\left(2\alpha -1\right)\frac{\pi }{4}\right],\sin \left[\left(2\alpha -1\right)\frac{\pi }{4}\right]\right)\alpha =5,6,7,8\hfill \end{array}$ (5)

Figure 1. Nine base vectors in the D2Q9 lattice model

图1. D2Q9格子矢量模型图

同时权重 ${\omega }_{\alpha }$ 可表示为

${\omega }_{\alpha }=\{\begin{array}{l}\frac{4}{9}\alpha =0\hfill \\ \frac{4}{9}\alpha =1,2,3,4\hfill \\ \frac{1}{36}\alpha =5,6,7,8\hfill \end{array}$ (6)

当求得粒子密度的分布后，流场的密度、速度和压力可定义如下：

$\rho ={\displaystyle \underset{\alpha }{\sum }{f}_{\alpha }},u=\frac{{\displaystyle \underset{\alpha }{\sum }{f}_{\alpha }{e}_{\alpha }}\text{+}f\delta \text{t}}{\rho },p=\rho c_s^2$ (7)

本文采用的光滑函数的二维形式可表述为：

$\delta \left(x-X\left(s,t\right)\right)=\frac{1}{\Delta x\Delta y}\varphi \left(\frac{x\text{-}X}{\Delta x}\right)\varphi \left(\frac{y-Y}{\Delta y}\right)$ (8)

式中 $x,y$ 分别表示为空间位置矢量 $x$ 的坐标分量， $X,Y$ 分别表示为拉格朗日坐标矢量 $X$ 的坐标分量，函数 $\varphi$ 可表示为

$\varphi \left(r\right)=\{\begin{array}{l}\left[1\text{+}\cos \left(\text{π}r/2\right)\right]/4,\left|r\right|<2\\ 0\left|r\right|\ge 2\end{array}$ (9)

2.2. 数值方法

假如固体(浸入)边界由一系列的拉格朗日点 $X_B^i\left(i=1,2,\cdots ,M\right)$ 离散,整个物理域由固定的等距的格子网格点 $x_j\left(j=1,2,\cdots ,N\right)$ 离散，格子网格间距 $\Delta x=\Delta y=h$ 。为此，可定义拉格朗日点上物理量与格子网格点上信息转换矩阵 $C_{ji}$

$C_{ji}=C\left(X_B^i-x_j\right)=\frac{1}{h^2}\varphi \left(\frac{X_B^i-x_j}{h}\right)\varphi \left(\frac{Y_B^i-y_j}{h}\right)$ (10)

等式(4)的离散形式可表示为

$f\left(x_j,t\right)={\displaystyle \underset{i}{\sum }{C}_{ji}}F\left(X_B^i,t\right)\Delta s_i\left(i=1,2,\cdots ,M;j=1,2,\cdots ,N\right)$ (11)

式中 $\Delta s_i$ 为第 $i$ 段边界的面积。令

$\begin{array}{l}u\left(x_j,t\right)=u^{\prime }\left(x_j,t\right)+\Delta u\left(x_j,t\right)，\\ u\text{'}\left(x_j,t\right)={\displaystyle \underset{\alpha }{\sum }{f}_{\alpha }{e}_{\alpha }}/\rho ，\end{array}$ (12)

则有

$\Delta u\left(x_j,t\right)\text{=}f\delta \text{t}/\rho$ (13)

式(11)代入(13)式，得到

$\Delta u\left(x_j,t\right)={\displaystyle \underset{i}{\sum }{C}_{ji}}F(X_B^i,t)\Delta s_i\delta t/\rho \left(i=1,2,\cdots ,M;j=1,2,\cdots ,N\right)$ (14)

为满足流固界面的无滑移边界条件，通过速度 $u_j$ 和 $\delta \left(x\text{-}X\left(s\text{,}t\right)\right)$ 近似光滑函数得到的固体边界拉格朗日点上的速度 $u\left(X\left(s_i\right)\right)$ 应该等于给定的固体边界的自然速度 $U\left(X_B^i,t\right)$ ，即

$U\left(X_B^i,t\right)={\displaystyle \underset{j}{\sum }{C}_{ji}^T}u\left(x_j,t\right)h^2\left(j=1,2,\cdots ,N;i=1,2,\cdots ,M\right)$ (15)

式中， $C_{ji}^T$ 表示 $$ 的转置矩阵。将式(12)和式(14)代入式(15)，可得

$\begin{array}{c}U\left(X_B^i,t\right)={\displaystyle \underset{j}{\sum }{\displaystyle \underset{i}{\sum }{C}_{ji}^T\Delta S_i{C}_{ji}}F\left(X_B^i,t\right)\delta t}{h}^2/\rho \\ +{\displaystyle \underset{j}{\sum }{u}^{\prime }\left(x_j,t\right)}{C}_{ji}^T{h}^2\left(i=1,2,\cdots ,M;j=1,2,\cdots ,N\right)\end{array}$ (16)

过式(16)，可求得固体边界力密度 $F\left(X_B^i,t\right)$ ，然后代入式(14)，可求得修正速度 $\Delta u\left(x_j,t\right)$ ，由式(12)，可求得下一步速度 $u\left(x_j,t\right)$ 。

3. 数值算例

图2为IB-LBM模拟圆柱主动旋转模型图。求解区域为一个长 × 宽 = $\text{15}D\times 10D$ 的矩形区域。圆柱直径为 $D$ ，圆心坐标为 $\left(-5D,-5D\right)$ 。 $\nu$ 表示运动粘度系数， $\nu =UD/\mathrm{Re}$ ，本例中 $\mathrm{Re}=100$ 。流体从左侧边界均匀流入，边界条件为： $u=U$ ， $v=0$ ；上下边界为无穿透边界，满足 $u=U$ ， $v=0$ ；右边界为流体流出边界，满足 $\partial u/\partial x=0$ ， $\partial v/\partial y=0$ ，圆柱固体边界以角速度 $\Omega$ 逆时针主动旋转。流场的网格划分为均匀的四边形网格，网格步长为 $\Delta x=\Delta y=0.025D$ ，时间步长为 $\delta t=1.0$ 。

表1为 $\Omega =0$ 即圆柱静止时升力系数、阻力系数和Strouhal数与其他文献计算结果的对比。从表可见，本文计算得到的升力系数和阻力系数略小于其他文献计算的结果，Strouhal数稍微大于其他文献计算的结果，总体上是吻合的，证实本文计算方法是可行的。

图3为圆柱在不同角速度下主动旋转时升、阻力系数随时间的变化图。由图可见，1) 在 $\Omega$ < 4 U/D时，升、阻力系数呈现出良好的周期性，说明流动尽管受到圆柱自旋的扰动，但绕流仍发生稳定的涡脱落现象。在 $\Omega$ = 4 U/D时，阻力系数的周期性遭到破坏，可能出现次频率，意味着当圆柱以更高的速度旋转时，诱发局部小涡结构的脱落；2) 升力系数随圆柱旋转角速度增大而增大，而阻力系数随圆柱旋转角速度增大而减小，意味着随着圆柱旋转角速度增大，圆柱绕流升阻比会逐渐增加，有利于圆柱的升降运动和向前运动，这与实际物理运动规律是吻合的。更详细的升、阻力系数计算结果的统计值见表2，由表可见，在 $\Omega$ < 4 U/D时，阻力系数的平均值是随圆柱旋转角速度的增大而减小，而阻力系数的幅值是随圆柱旋转角速度的增大而增大。但升力系数的平均值和幅值都是随圆柱旋转角速度的增大而增大。同时，升、阻力系数的均方根都随圆柱旋转角速度的增大而增大，升阻比随圆柱旋转角速度的增加而快速增加。

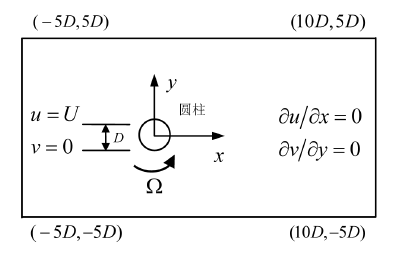
Figure 2. Computational zone and boundary conditions

图2. 计算区域与边界条件

Table 1. The numerical reslts compared with that of other papers at Ω = 0 with Re = 100

表1. Ω = 0，Re = 100的计算结果与其他文献的对比

Table 2. Drag and Lift coefficient statistics for the flow over a circular cylinder at Re = 100 under different rotating velocity

表2. Re = 100时，圆柱不同旋转角速度下升、阻力系数计算结果统计值

(a) 升力系数 (b) 阻力系数

Figure 3. Drag and Lift coefficients against time under different rotating velocity of cylinder

图3. 圆柱不同角速度下阻力和升力系数随时间的变化

图4为不同角速度下主动旋转时升力系数最大时刻时所对应的涡核中心位置图，在Ω < 4 U/D时，由图可见正负涡核间的距离随着圆柱旋转角速度的增加也有逐渐增大的趋势。图5为圆柱在不同角速度主动旋转时升力系数最大时所对应的涡量图。由图可见，随着圆柱旋转角速度的增大，尾涡结构的拉伸能力增加，尾涡形状变得越扁平，在Ω = 4 U/D时，明显看见交错的正负涡结构已经变成上下排列大致平行的尾涡结构。

4. 结论

本文将一种隐式直接力方法与格子Boltzmann方法有机结合，通过格子Boltzmann方法计算流场，

Figure 4. The distance between the eyes of vortex under different rotating velocity of cylinder

图4. 圆柱不同角速度下尾涡正负涡核间的距离

Figure 5. Isolines of vorticity for the flow over a circular cylinder at time of maximum lift coefficient under different rotating velocity for Re = 100, range: $-16\le {\omega }_{z}D/U_0\le 16$ , intervals are 0.16

图5. 雷诺数100时，圆柱不同旋转角速度下对应最大升力系数时的涡量图，涡量范围： $-16\le {\omega }_{z}D/U_0\le 16$ ，等值线间隔：0.16

通过浸入边界法考虑动边界问题，让固体边界的校正速度等于给定的固体边界的自然速度, 求得固体边界离散点的作用力密度。同时对近壁区速度给出二次速度修正方法。利用VC++编写相应的数值计算程序，并以圆柱主动旋转为基准数值算例，通过与其他文献的比较，验证了基于二次速度修正的浸入边界-格子Boltzmann方法的准确性和可靠性。研究还发现随着圆柱旋转角速度的增加，正负涡核间的距离有逐渐增大的趋势，同时圆柱绕流升阻比会逐渐增大，有利于圆柱的升降运动和向前运动。

基金项目

国家自然科学基金项目(51479085, 11262008)；霍英东青年基金项目(141120)。

NOTES

^*通讯作者。