1. 引言
交通状态预测解决如何在带有随机性和不确定性的交通变化中,根据多源异构的交通流数据,结合其他影响因素,进行数据的系统分析,找出其中的规律并建立相应的预测方法和模型,以预测未来的交通状态变化 [1] [2] 。短时交通状态预测的方法主要包括两类:构建以传统数学与物理方法为基础的预测模型和以现代科学技术与方法(如仿真技术、人工智能、控制理论)为基础的预测 [3] 。
随着数据挖掘技术的发展与成熟,K邻近算法(KNN算法)具有结构简单、计算效率高的特点,获得越来越多的关注与研究 [4] 。KNN算法的相合性和收敛性在文献 [5] 中得到有效验证;文献 [6] 与 [7] 利用高速公路收费站的进出口数据,根据全天不同时段的交通状况特征进行历史数据分段,采用KNN算法实现高速公路短期行程时间预测;另一方面,KNN算法易于与其他算法如核曲线(N-Curve)相结合,实现不同近邻的短时行程时间预测 [8] ;然而,以上研究路段都是状态平稳的高速公路,缺乏对具有较高随机性与不确定性的城市道路的KNN算法预测框架的研究与分析。
针对上述问题,本文提出基于KNN算法的短期预测框架,并提出差分向量作为特征向量的扩充以考虑交通状态的急剧变化;结果表明,对比支持向量与随机森林方法,增加差分序列的KNN算法适合预测非线性变化的交通流,实现更高精度的城市短时交通状态预测。
2. 基于KNN算法的预测框架构建
2.1. KNN算法
KNN算法是数据挖掘技术中的分类方法之一,基于实例学习的非参数预测思想,通过搜索历史数据库中与待预测特征向量最相似的K个记录来进行分类。如果一个样本在特征空间中K个最相似(即特征空间中最近邻)的样本中的大多数属于某一个类别,则该样本也属于这个类别。换句话说,KNN算法中所选择的近邻样本都是已经正确分类的对象,并只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。如图1所示,在某一特征空间存在w1,w2,w3三个分类,通过计算某一样本X的所有历史样本的度量距离,寻找K个最邻近历史样本。图中样本X的5个最邻近历史样本中,有3个从属于分类w1,有2个从属于分类w3,因此确定样本X从属于分类w1。
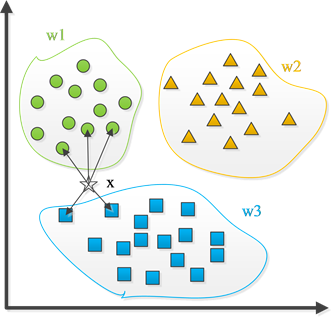
Figure 1. The classification diagram of KNN method
图1. KNN算法分类演示图
2.2. 基于KNN算法的预测框架
基于KNN算法实现预测,主要思路与分类方法类似,认为系统的所有因素之间的内在联系都蕴涵于历史数据中,能够直接从历史数据中得到预测信息,而不是根据历史数据建立一个近似的预测模型。因此,KNN算法通过寻找与当前特征向量最相似的K个历史特征向量,当前时刻的预测值由这K个历史特征向量指向值的加权决定。框架流程图如图2所示。
预测框架首先从在线数据库获取当前时刻的特征向量,按照当前时刻的历史分段,匹配历史数据库,计算描述实时特征向量与历史特征向量之间差异的度量距离值;接着由距离最小的K个特征向量指向的预测值,经过加权平均后得到预测值并写入在线数据库;最后按照15分钟为时间间隔滚动向前预测,实现实时短期交通预测。
2.2.1. 数据预处理
KNN算法的预测精确度很大程度上由历史数据集的质量决定,一个数据充沛、完善、采样率合适的历史数据集是KNN准确预测的前提条件。本文采用出租汽车GPS (Global Positioning System)、百度导航与公交车GPS三者融合得到的速度结果数据,数据分辨率为5分钟。总体数据样本较充足,但存在以下三个问题:
历史数据量大导致预测计算量大;
部分路段存在某些时间片数据缺失;
少数偏远区域的路段数据样本量严重不足。
因此,将原先5分钟的时间分辨率转换为15分钟,压缩数据量,提高数据的有效性,并对某些历史数据缺失的路段进行线性插值处理。
2.2.2. 确定特征向量
KNN算法的特征向量,不仅需要与待预测的交通状态具有较强的相关性,能反映历史数据集合中的个体间差异,同时在预测过程中还需要及时从实时数据中获取以满足在线短时预测的要求。由于待预测的平均速度具有时间序列自相关性,因此本文选择平均速度的时间序列作为当前时间点的特征向量,即
(1)

Figure 2. The prediction framework of KNN method
图2. 基于 KNN算法的预测框架
其中,
表示t时间点的特征向量,
表示t − 1时间点的平均速度,n表示特征向量的个数。由于前3个时间点的平均速度与当前平均速度的相关系数最高,因此,上式中的n = 3,即特征向量中平均速度的个数为3个。
此外,仅使用前3个平均速度的时间序列作为的特征向量,可能导致KNN算法无法识别平均速度的变化趋势,无法在随机性较大的城市路段进行准确预测。因此本文增加差分向量作为特征向量的补充,目的是让KNN算法能够识别平均速度的变化趋势,提高特别是对于城市道路的预测准确性与适用性。差分向量
由前后两个时段的平均速度的差值构成,即:
(2)
(3)
2.2.3. 历史数据分段
实际预测应用的时间段主要集中在6:00至24:00。考虑到工作日与休息日,以及早高峰、晚高峰、平峰期间路段交通状况的差异性,历史数据集分为6类,分别是:工作日早平峰、工作日早高峰、工作日午平峰、工作日晚高峰、工作日晚平峰、休息日全天等6个时间段,其中正常工作日为周一到周五,休息日为周六与周日。具体分割如图3所示。历史数据的分段,将KNN算法集中在最为可能的历史交通状态中搜索,避免极为不吻合的特征向量的匹配,可以有效提高实时预测效率和精确度。
2.2.4. 确定距离度量
本文采用欧式距离衡量实时特征向量与历史特征向量之间的差异,即:
(4)

Figure 3. The historical data subsection of KNN prediction
图3. 历史数据分段—KNN预测
其中,
表示实时特征向量与历史特征向量之间的欧式距离,a为整数,范围为[1, N],N表示分段历史特征向量的个数;
表示平均速度的时间序列之间的权重向量,越靠近当前时间点的权重越大,本文取
;
分别表示前n个时间点的实时平均速度与历史平均速度,
分别表示前n个实时速度差分与历史速度差分。
2.2.5. K值的标定
K值是KNN算法中的唯一参数,其取值直接影响模型预测的结果。不同道路类型、不同时段实现精确预测的K值是不相同的。因此,本文采用交叉验证的方法进行K值的标定,具体步骤如下所示:
步骤1:设K的最大值与最小值分别为
和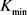 ,并令
;
,并令
;
步骤2:取出某一路段一个月的历史数据集,将前24天的数据作为训练数据集,后7天的数据作为测试数据集,按照图3的KNN预测的框架进行预测,计算预测值与观测值之间的绝对平均百分比误差(MAPE, Mean Average Percentage Error):
(5)
其中, 表示在t时间点的观测平均速度,
表示在t时间点的观测平均速度, 表示在t时间点的预测平均速度。接着统计7天内所有时间点的平均MAPE,作为当前K值的评价指标,即:
表示在t时间点的预测平均速度。接着统计7天内所有时间点的平均MAPE,作为当前K值的评价指标,即:
(6)
步骤3:计算所有K值的评价指标;
步骤4:取平均MAPE最小的对应的K值,作为该路段标定后的K值。
2.2.6. 确定下一时刻预测值
确定K值后,取前K个欧式距离最小的历史特征对应的历史值作为备选预测值,通过加权估计来预测下一时刻的平均速度。加权的原则认为当某个历史特征向量的K值越小时,该历史特征向量对当前的预测具有更大的影响,具体加权的估计方法为:
(7)
其中,
表示当前时间点的预测值,
表示K个备选预测值中的第n个,
表示第n个备选预测值的权重值,其计算方法如下式所示 [5] :
(8)
其中,
表示K个备选预测值对应的欧式距离中的第n个。
2.2.7. 滚动预测
滚动预测模型在交通状态实时预测中有着广泛的应用 [9] [10] ,它能根据传回的实时数据与当前的预测结果,持续对路段情况进行实时预测。本文采用两层滚动嵌套,第一层的嵌套基于当前时间点,向前预测一定步长的滚动预测;第二层嵌套是向前一个时间点的滚动预测。
第一层滚动预测嵌套如图4(a)所示,以t为7:00为例,首先获得当前时间点绿色框体的实时数据,即6:15~7:00时间段内的以15分钟为分辨率的前3个平均速度组成的时间序列;然后将实时数据输入到KNN的预测框架中,完成红色框体内待预测的时间范围,即往后15分钟;完成循环1后,整体时间段向前滚动15分钟的步长,将上一个循环的前3个平均速度的时间序列作为下一次循环的“实时数据”,输入到KNN预测框架中,继续向前预测15分钟,直到完成整个预测时长,即1个小时。
第二层嵌套如图4(b)所示。图中循环1表示已经完成了第一层嵌套,即向前预测了1个小时;此时,向前滚动一个15分钟的步长,等待下一个15分钟的实时数据输入到KNN预测框架中,完成下一个1小时的预测,直到预测的时间结束点(T为24:00)。
3. 实例验证
本实例用于验证KNN预测框架实现不同类型城市道路短时交通预测的能力,比较两类特征向量的预测精度,验证差分特征向量的适用性。以深圳市为例,随机挑选40条路段,高速路、快速路、主干路、次干路等不同类型路段各10条;时段为2016年7月1日至2016年7月30日,共30天的数据,其中前23天的数据作为KNN预测框架的训练数据集,后7天的数据作为测试数据集。预测的时段从早上6点至晚上24点,每次往后预测1个小时。预测间隔为15分钟。
为了分析KNN算法在不同道路类型的不同预测效果,本文分别从4个道路类型中随机抽取一条路段作为典型路段进行具体分析,各个路段的具体信息如表1所示。
 (a)
(a)  (b)
(b)
Figure 4. The double-loop rolling prediction of KNN method. (a) Is the first rolling; (b) Is the second rolling
图4. 双层滚动预测嵌套—KNN预测。(a) 第一层嵌套;(b) 第二层嵌套

Table 1. The basic information of typical road section
表1. 典型路段的基础信息
3.1. K值标定
K的最小值设定为1,最大值设定为50。各条典型路段的标定结果如图5所示。
图5中纵轴表示测试天的所有预测点的平均MAPE,横轴表示K值的大小。从图中看出,K值的选取在很大程度上影响KNN预测框架的精确度。所有路段的预测MAPE都随着K值的增大而减少,其中K为1时预测的精度最差。具体地,典型高速路和快速路在K值分别取23和18的时候精确度最高,而典型主干路和次干路则在K值取23和45时精确度最高。考虑到不同K值下的误差下降幅度及计算效率的平衡,实例中的K值统一取图5的拐点处,即K = 10的红线处。
3.2. 所有路段预测结果
根据提出的KNN算法的框架,对深圳市40条路段进行短期交通状态预测。预测的结果如图6所示。
预测结果表明,基于KNN算法的预测框架,能够精确地预测城市不同道路类型的路段平均速度,并且预测的MAPE都低于20%。快速路与高速路的预测是最为精确的,预测平均MAPE分别为7.93%与8.64%,原因是快速路和高速路道路状况较为简单,没有红绿灯的阻断作用,正常情况下交通运行均较为平稳。主干路和次干路得平均MAPE分别为10.28%和16.42%,原因在于主干路和次干路存在红绿灯、公交临时停靠、行人过街等复杂情况,交通状况较为复杂,容易产生对交通的临时阻断,偶发异常发生概率较高,因此预测精度相对下降。
3.3. 特征向量的比较
本项实验将对比分析含差分序列和不含差分序列的KNN的预测特性,并详细分析各类道路类型在每一时间点的预测精度,一周的预测统计结果如表2所示。实验结果表明不同道路类型交通状态的变化程度大小在一定程度上影响KNN预测框架的精确度,含差分序列的KNN预测框架能够更好地适应交通状态的急剧变化,呈现更小的预测误差:主要原因是差分序列能够直观地量化与捕捉前后时间点的速度变化,通过欧氏距离的计算能够精确匹配到历史数据库中速度变化相似的情况,准确预测下一个时间点的交通状态,提高KNN模型识别交通状态变化的能力。下文将具体分析各个道路类型的预测结果。
3.3.1. 高速路与快速路
高速路与快速路的日平均MAPE最高与最低的预测折线图如图7所示。图中左纵轴为MAPE,表示某个时间点往后预测1个小时的平均MAPE;右纵轴为平均速度,表示某个时间点的路段平均速度,单位为千米每小时;横轴为时间点,时间间隔为15分钟。
7月24日(周日),高速路与快速路在前段时间维持较高的预测精度。然而,高速路的预测误差突然随着路段平均速度的骤降急剧增大,原因在于路段发生了交通事故,对应时段的历史数据集中没有对应的历史交通状态信息。但是,增加差分序列后,KNN能够在这时间段内很好地识别出当前交通状态的急剧变化,及时调整预测值,尽可能提高预测精确度。快速路同样在晚间平均速度下降时预测误差稍微
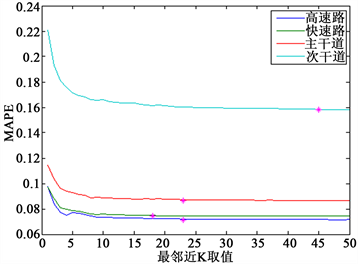
Figure 5. The calibration results of tipycal road section
图5. 典型路段标定结果图
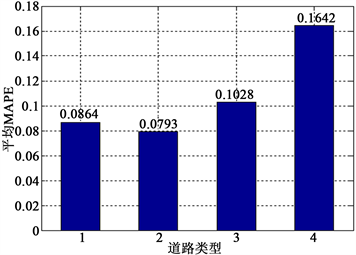
Figure 6. The prediction hisrogram of MAPE
图6. 预测MAPE柱状图(其中道路类型为1、2、3、4表示高速路、快速路、主干路、次干路。“0.0864”表示10条高速路的平均预测MAPE为8.64%)

Table 2. The KNN prediction MAPE of different types of road sections
表2. KNN预测不同道路类型的预测MAPE结果

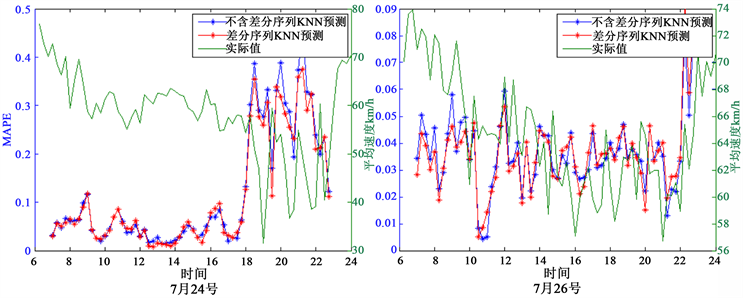
Figure 7. The prediction line chart of freeway (up) and expressway (down)
图7. 高速路(上)与快速路(下)的预测折线图
上升,与发生交通事故的高速路不同,该时段是快速路周期性变化的晚高峰,历史数据集中包含丰富的对应的交通状态信息,KNN算法能够从中精确匹配并预测往后的交通状态,增加差分序列后KNN识别变化交通状态的能力得到了相应的加强。
高速路与快速路在7月26日(工作日)分别维持较高的预测精度,原因是当天路段的平均速度变化较为平稳,具有明显的规律性,平均速度的变化幅度较低,KNN预测框架能够在平稳的交通状态下准确预测未来短时交通状态。
3.3.2. 主干路与次干路
主干路与次干路的平均预测误差高于10%,日平均MAPE最高与最低的预测折线图如图8所示。
主干路两天的交通变化都较为平稳且具有明显规律性,MAPE在10%左右波动。由于主干路的平均速度变化幅度较大,预测精确度有所下降,但仍能维持在10%左右,在交通状态变化频繁且剧烈的路段,含有差分序列的特征向量能够增强KNN预测的精确度。
与主干路相比,次干路的路段平均速度低,但变化幅度大,预测的精确度较差,原因是次干路车道数较少,受车辆临停、公交车停靠等因素的影响较大,并且次干道存在部分历史时间片数据缺失的情况,部分次干路的历史数据完整性不足,特征向量不能准确地描述当前的交通状态,因此预测的准确性较低。
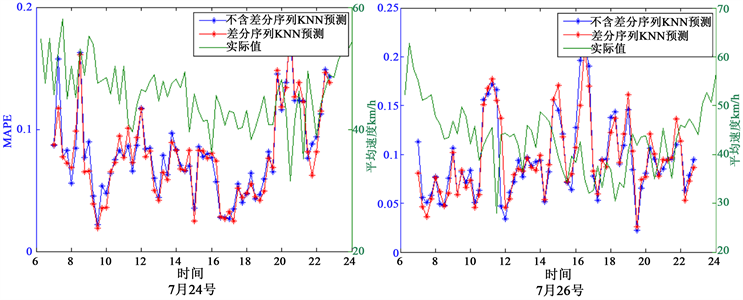

Figure 8. The prediction line chart of arterial road (up) and sub-arterial road (down)
图8. 主干路(上)与次干路(下)的预测折线图
3.4. 与其他预测算法的对比
针对预测精度较低的次干道,选择相同的特征向量,分别采用含差分序列的KNN、不含差分序列的KNN、支持向量机(Support Vector Machine,SVM)、随机森林(Random Forest,RF)等四类方法进行7月26号的短时交通预测,统计的MAPE分别为18.22%、18.82%、20.39%、19.04%,表明在该数据集下含差分序列的KNN算法具备最优的预测能力。其中可能的原因是KNN算法在数据集质量较差的情况下能更好地适应变化频繁且剧烈的交通状态。
另一方面,上述四类算法的单步预测与观测数据的速度折线图如图9所示。从图中看出,四类算法的预测结果均滞后于观测数据,其中SVM的预测波动最大,与观测数据的偏离幅度最大。另一方面,RF的预测结果呈现较为稳定的状态,变化幅度较小,但不含差分序列的KNN算法的预测结果比SVM与RF更为精确,表明在缺乏数据与交通状态变化剧烈的次干道中,KNN算法能够获得更精确的预测结果。此外,增加差分序列是提高KNN算法的预测精度的有效特征之一。
4. 总结
研究提出了基于KNN算法的交通状态预测框架,以平均速度的时间序列作为特征向量,引入差分

Figure 9. The prediction line chart of different algorithms
图9. 多种算法的预测折线图
序列作为补充,预测城市交通不同道路类型的短时交通状态。实验结果表明,增加了差分序列的KNN预测框架能够更好地捕捉交通变化的规律,提高预测的精确度。此外,道路类型不同,KNN预测框架的预测结果也呈现一定差异性:
高速路的交通状态变化平稳,KNN的预测结果最为准确。但是,当高速路发生交通事故时,如果历史数据库中没有含有足够的相似信息,KNN的预测精度会急剧下降,这可作为发生交通事故的预警信息,这也是本文下一阶段的研究内容之一。
快速路与主干路的交通状态呈现较为明显的早晚高峰的特征,历史数据库中包含足够的特征信息,KNN的预测值与实际值的误差较小。此外,交通状态的变化幅度也是影响KNN预测精度的一个重要因素之一。交通状态变化幅度越大,KNN预测框架的预测精度越低。作为特征向量的补充向量,差分序列能够很好地增强KNN捕捉交通变化的能力,提高预测的精确度。
针对交通状态变化幅度最大的次干路,KNN算法能够及时跟上变化的交通状态,比SVM和RF预测算法获得更准确的预测结果,且差分序列是提高KNN预测精度的有效特征向量之一。
下一步计划添加天气、时间、节假日等其他因素丰富特征向量描述路段运行状态的维度。另一方面,深入研究全深圳市的路网特征与关系,引入交通流量的变化增强交通速度的预测能力。
致谢
感谢深圳市科技计划项目(项目编号GGFW2016033017241891,项目名称“深圳市交通大数据公共技术服务平台”)和深圳市战略性新兴产业发展专项资金2017年第一批扶持计划(项目名称:深圳市交通碳排放工程实验室,批复文号:深发改[2017] 550号)的资助。
基金项目
深圳市科技计划项目(GGFW2016033017241891),深圳市战略性新兴产业发展专项(深发改[2017] 550号)。
NOTES
*通讯作者。