1. 引言
光子晶体是一种介质呈周期性排列而成的新型光学人工结构。同半导体晶体由于周期势场作用而存在着结构电子能带结构类似,光子晶体由于介质的周期性排列而存在着光子能带结构 [1] [2] 。且能带与能带之间存在着带隙,也称为禁带,使得频率落在禁带内的电磁波无法在光子晶体中继续传播 [3] [4] [5] [6] 。一维光子晶体是禁带在一个方向上有取向的光子晶体,一维光子晶体的带隙具有极强的可调性,且容易制备 [7] [8] ,对一维光子晶体的研究具有实际应用价值。
掺镧锆钛酸铅(Lead Lanthanum Zirconate Titanate, PLZT)是一种极好的电光材料,具有明显的电光效应,而尤其是Pb0.865La0.09Zr0.65Ti0.35O3 (PLZT(9/65/35))具有极明显的二次电光效应 [9] 。一维掺镧锆钛酸铅光子晶体在没有外加电场作用时,由于介质的折射率是固定的,因此能带结构是不发生变化的。而当一维掺镧锆钛酸铅光子晶体被施以外加电场时,由于在外加电场的作用下介质掺镧锆钛酸铅的电光效应导致折射率发生变化,使得一维掺镧锆钛酸铅光子晶体的能带结构产生变化。利用有限元法计算了一维掺镧锆钛酸铅光子晶体的能带结构,并理论分析了电场变化对一维掺镧锆钛酸铅光子晶体的能带结构及禁带的中心波长和带宽的影响。本文选用掺镧锆钛酸铅这一电光效应明显且具有低成本、易制备等特点材料对一维光子晶体的电光特性进行研究,可为一维光子晶体测试仪器的应用提供理论准备。
2. 掺镧锆钛酸铅的电光效应
在外加电场作用下,掺镧锆钛酸铅具有极明显的二次电光效应,折射率变化如下 [10] [11] [12] [13]
(1)
式中,n、
分别表示掺镧锆钛酸铅的折射率及其变化,
为二次电光系数,E为外加电场的电场强度。若这里我们选取交流电场
,那么折射率变化与所加交流电场的时间之间的关系如图1所示。
3. 一维光子晶体有限元模型
在一维光子晶体均匀介质层中,电磁场必须满足亥姆霍兹方程:
(2)
其中,
是相对介电常数,
是相对磁导率
,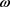 为频率,c为光速,
是电场E或磁场H。
为频率,c为光速,
是电场E或磁场H。
Figure 1. Effect of AC electric field on index change
图1. 交流电场对折射率变化的影响
满足亥姆霍兹方程最基本的解是平面电磁波解。
其解
的形式如下:
(3)
其中,
是布洛赫矢量。梯度算子变化的结果为
该问题可简化为:
(4)
有限元方法首先是区域离散化。根据一维光子晶体的结构,可以将晶体的每一个介质层作为一个单元。如果光子晶体有N个周期,那么就可以划分为2N个有限单元,每个单元的介质折射率和几何厚度交错相同。
然后是选择插值函数。为简单起见,我们可以应用线性插值,因此,在e个单元内,场值
可以近似为

式中,
和
是待定系数。每一单元内均有两个节点,根据两个节点处的值,可以解出
和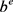 。得到
。得到
式中,
是单元插值函数,
。
由变分原理推导出式(4)的泛函可写成
(5)
式中,
,且
(6)
其中
和
分别是单元的两个结点所处的位置。然后取
对的
导数,最后写成矩阵形式
 (7)
(7)
应用局部和全局结点编码的关系,我们能够将
扩展成
矩阵,并将
扩展成
列向量,
扩展成
列向量。则有由所有单元相加后可写成下列矩阵形式
(8)
式中,
是
矩阵,
、
是
列向量,其中,
是与区域边界有关的矩阵。然后,通过高斯消元法求出各点的
值。此后再通过解后处理可以求得所需要的关系值。下面以电场为例,e单元内的有效反射系数为
(9)
式中,
为e单元内入射的电场,
为e单元的反射场。于是一维光子晶体的有效反射系数为
(10)
式中
表示最后一单元的反射系数,
为入射单元界面前处的有效反射系数,
为第e单元内的光程差,
,其中,
是光线在第e单元介质内的传播方向与界面法线方向之间的夹角,
和
分别为第e单元内的折射率和几何厚度,
是入射光的波长。由此可以得出透射率为
(11)
由透射谱便可得出一维光子晶体TE、TM模式下的能带图。
本文采用有限元法对一维光子晶体结构划分为多个有限单元进行研究,与采用传统的传输矩阵法相比,保证了研究结果的更趋可靠性。
4. 数值分析与结果
如图2所示的是一种典型的一维光子晶体,由介质A和介质B交替叠层而成。介质A的折射率为
,几何厚度为a,介质B的折射率为
,几何厚度为b,折射率空间变化周期(晶格常数)为
,且d的量级为光波长量级。
其中,介质A为掺镧锆钛酸铅(PLZT(9/65/35)),介质B为二氧化硅。且非磁性条件下满足
,
,其中,
、
分别掺镧锆钛酸铅(PLZT(9/65/35))和二氧化硅的折射率。选取a = 60 nm,b = 120 nm。中心波长为
,光入射角为30˚,周期数为N = 9。而
,二次电光系数
。
在没有外加电场作用时,电场强度E = 0 KV/cm,二维掺镧锆钛酸铅光子晶体的TE偏振模式和TM偏振模式的能带结构如图3中实线所示。当被施以外加电场时,如电场强度E为100 KV/cm,由于掺镧锆钛酸铅的电光效应导致折射率发生变化,一维掺镧锆钛酸铅光子晶体的能带结构随之发生变化,能带结构如图3中虚线所示。
下面就电场变化对一维掺镧锆钛酸铅光子晶体的禁带的中心波长及带宽进行分析。一维掺镧锆钛酸铅光子晶体的TE偏振模式和TM偏振模式的禁带的中心波长及带宽与电场的关系如图4和图5所示。
由图4和图5表明,在TE偏振模式下,对于禁带中心波长与电场关系为四次方函数关系,系数分

Figure 2. Schematic diagram of 1-D photonic crystal
图2. 一维光子晶体示意图
Figure 3. Effect of electric field on 1-D PLZT photonic crystals band structure. (a) TE; (b) TM
图3. 电场对一维掺镧锆钛酸铅光子晶体能带结构的影响。(a) TE;(b) TM
别为1.2 × 10−6、−1.5 × 10−4、−1.2 × 10−3、−6.3 × 10−2、6.4 × 102;禁带宽度与电场关系为四次方函数关系,系数分别为6.9 × 10−6、1.0 × 10−3、−6.0 × 10−3、6.9 × 10−1、2.2 × 102。在TM偏振模式下,对于禁带

Figure 4. Effect of electric field on central wavelength of band gap. (a) TE; (b) TM
图4. 电场对禁带中心波长影响。(a) TE;(b) TM
中心波长与电场关系为四次方函数关系,系数分别为7.1 × 10−6、−1.2 × 10−4、−1.9 × 10−3、−8.3 × 10−2、6.5 × 102;禁带宽度与电场关系为四次方函数关系,系数分别为1.6 × 10−6、−3.2 × 10-4、6.1 × 10−3、−3.2 × 10−1、2.5 × 102。
因此,随着外加电场的电场强度的增大,无论是TE偏振模式还是TM偏振模式,一维掺镧锆钛酸铅光子晶体的中心波长都向反波长方向飘逸,禁带宽度逐步减小。然而每个禁带的起始波长的漂移量与截止波长的漂移量并不相同,不同禁带宽度随电场的变化也是不同的,电场变化对截止波长的影响程度大于起始波长的影响,且禁带的中心波长及带宽宽度的变化与电场强度基本上呈四次方函数关系。这与禁带的中心波长与介质的介电常数变化呈线性关系而介电常数变化与电场强度呈四次方关系是一致的。
5. 结论
利用有限元法计算了一维掺镧锆钛酸铅光子晶体的能带结构,并从掺镧锆钛酸铅的电光效应出发,分析了一维掺镧锆钛酸铅光子晶体的能带结构与电场间的关系。结果表明,随着外加电场的电场强度的增大,由于电场的变化引起了掺镧锆钛酸铅的折射率的变化,一维掺镧锆钛酸铅光子晶体的能带结构整体向高频频方向漂移,禁带的漂移量与电场强度呈四次方函数关系。
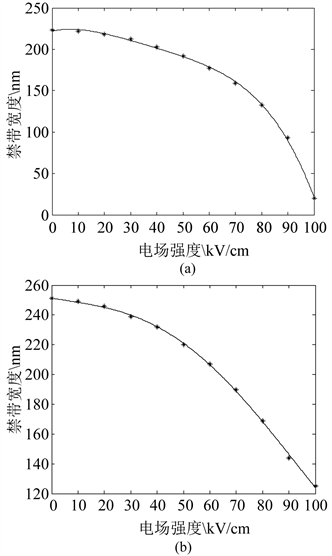
Figure 5. Effect of electric field on band gap. (a) TE; (b) TM
图5. 电场对禁带宽度影响。(a) TE;(b) TM
基金项目
浙江省科技创新活动计划资助项目(2016R424002)资助。
NOTES
*通讯作者。