基于长短基线法的整周模糊度解算算法

Integer Ambiguity Resolution Algorithm Based on Different Baseline Method

摘要: 利用载波相位观测值可以大大提高导航定位精度，但整周模糊度的存在会严重影响结果准确性。本文分析了LAMBDA算法解算整周模糊度的优缺点。针对其构建搜索域导致的搜索时间较长的问题。提出了一种基于长短基线结合的整周模糊度解算算法。通过对比LAMBDA算法与长短基线法解算精确度以及解算速度进行分析对比。通过仿真实验可以看出，LAMBDA法的解算速度相对于长短基线法来说较慢，但是在卫星与接收天线之间呈一定角度时，长短基线法会会大大的提高模糊度解算的误差。本文还粗略地分析了长短基线法引起误差的原因。

Abstract: Carrier phase observation can greatly improve the accuracy of navigation and positioning, but the existence of ambiguity will seriously affect the accuracy of the results. This paper analyzes the ad-vantages and disadvantages of LAMBDA algorithm for integer ambiguity resolution. The problem of constructing search domain leads to long search time. An algorithm of integer ambiguity resolution based on long baseline and short baseline is proposed. By comparing the LAMBDA algorithm with the long baseline method, the accuracy and speed of calculation are analyzed and compared. The simulation results show that the LAMBDA method is slower than the long-short baseline method, but when the angle between the satellite and the receiving antenna is certain, the long-short baseline method will greatly improve the ambiguity resolution error. The causes of errors caused by the long baseline method are also roughly analyzed.

1. 引言

卫星导航定位技术根据信号的不同可以分为伪距观测方式与载波相位观测方式。伪距观测受误差影响较大会导致测量的误差较大，无法运用在高进度的姿态测量的需要，所以，高精度的姿态测量一般使用载波相位观测方式。

载波相位观测通过卫星信号与接收机振荡器产生的参考载波信号之间相位差进行跟踪来确定站星之间的距离，并完成对天线位置的确定。

但是，由于接收机的鉴相器无法通过当前的相位值来获得载波在导航卫星及地面接收站天线之间间隔了多少整数个波长。此时的载波相位解算就会出现一个未知量，这个未知量被称之为载波相位观测整周模糊度。整周模糊度的存在对载波相位观测值的准确性有着很大的影响。为了获得更准确的导航信息，就需要精度更高的载波相位观测值。

整周模糊度解算可以分为两大类，一种是利用观测设备的移动和观测卫星变化所带来的有效信息，称为基于运动的载波相位整周模糊度解算算法。另一种是利用载波相位值对整周模糊度数进行最优化估计的过程。运用最为广泛的主要是基于最小二乘算法及其改进算法，包括FARA、Cholesky分解法、快速模糊度搜索滤波FASF法、LAMBDA方法等。最早的基于搜索域的整周模糊度解算算法的是整数最小二乘法，通过利用载波相位观测值以及基线的信息构造出一个模糊度搜索的范围用于搜索，但是由于整周模糊度之间的相关性较强导致搜索范围被过分拉长，导致搜索效率较低。为了解决问题，提出了其他的基于整数最小二乘的算法进行改进。

现阶段，整周模糊度解算主要是基于搜索域的搜索算法，LAMBDA算法是目前来说应用最广泛且解算成功率及效率很高的一种方法。其主要思想是基于最小二乘方法的搜索方法。通过对基于最小二乘搜索法中出现的协方差矩阵进行处理，降低模糊度相关性，以此来提高搜索的效率。

现阶段整周模糊度解算算法的主要研究方向主要是为：1) 针对解算方程病态问题构造相应的正则化矩阵来提高解算的精确度 [1] [2] 。2) 利用约束来缩小搜索的范围，降低搜索的复杂度，提高搜索效率 [3] 。

LAMBDA [4] 算法虽然能较为精确的获得计算的结果。但是由于需要多个历元的结果来构造搜索域，才能进一步的完成搜索的工作，不利于载波相位的实时解算。

在整周模糊度求解的过程中，短基线能较快的解算出整周模糊度的结果，但是相对的精确度较低，长基线的精度较高，但是解算的难度较高。而在本地坐标系下，基线向量的三个分量与飞行器的姿态角以及长度有关，对于长短不同的两条共线基线来说，基线向量之间是整数倍的关系。利用两两条基线向量之间的关系，利用较短天线来快速求解出模糊度的粗略值，再用长基线的倍数关系来提高解算的精度。

本文通过分析载波相位定位技术的基本原理及整周模糊度搜索的算法，主要是LAMBDA算法。并进行了相应的MATLAB仿真，比较了LAMBDA算法以及长短极限法下整周模糊度搜索域即搜索性能，可以为整周模糊度解算方案的选择提供参考依据。

2. LAMDBA算法原理

载波相位观测模型 [5] 如式所示，其中 $y$ 是 $m$ 维载波相位观测量， $a$ 、 $b$ 分别为 $n$ 维， $t$ 维的未知参数向量， $A$ 、 $B$ 为相应的系数矩阵， $v$ 是观测误差。 $a$ 主要是载波相位的整周模糊度 [6] 的参数向量，且 $a\in Z^n$ 、 $b$ 是包含基线向量、电离层、对流层误差的参数向量，并且 $b\in R^t$

$\begin{array}{l}y=Aa+Bb+v\\ a\in Z^n,b\in R^t\end{array}$ (1)

由于 $a$ 、 $b$ 都是需要估计的参数，最小二乘算法的核心是通过对观测方程的处理 [4] ，尽量降低噪声和误差对测量精度的影响。原理是利用最小化误差平方，来求解出令误差平方最小的参数解

通过最小二乘法求出满足误差平方最小的参数 $a$ 、 $b$ 。由于在求解的过程中忽略了参数的整数特性，求解整周模糊度就需要在获得浮点解 $\hat{a}$ 、 $\hat{b}$ 的基础上，对模糊度的值进行搜索。此时的最小二乘就转化为：

$\begin{array}{l}\underset{a,b}{\min }{\Vert y-Aa-Bb\Vert }_{Q_y}^2=\underset{b}{\min }{\Vert \stackrel{⌢}{b}-b\Vert }_{Q_{\stackrel{⌢}{b}}^{-1}}^2+\underset{a}{\min }{\Vert \hat{a}-a\Vert }_{Q_a^{-1}}^2\\ a\in Z^n，b\in R^t\end{array}$ (2)

对于向量 $b$ 来说，由于没有约束条件，只需要寻找到满足 $\underset{b}{\min }{\Vert \stackrel{⌢}{b}-b\Vert }_{Q_{\stackrel{⌢}{b}}^{-1}}^2$ 条件的 $b$ 即可，而且矢量 $a$ 和 $b$ 并无关联。让中 $\stackrel{⌢}{b}\text{=}b$ 即可。通过改变整数 $a$ 使 ${\Vert \hat{a}-a\Vert }_{Q_{\stackrel{⌢}{a}}^{-1}}^2$ 最小，此时的 $a$ 就是整周模糊度解算的候选模糊度解。

整数最小二乘估计算法解算算法通常分为两步 [7] ：

首先忽略 $a$ 的整数约束，利用一般最小二乘法估计出 $a$ 与 $b$ 的浮点解 $\hat{a}$ 、 $\hat{b}$ 及其协方差矩阵：

然后利用浮点解搜索使目标函数最小的整数作为整周模糊度固定解 $\hat{a}$ 。在进行搜索求解时，搜索空间的表示为

${\left(\hat{a}-a\right)}^T{Q}_a^{-1}\left(\hat{a}-a\right)\le {\chi }^2$ (3)

式(7)是一个 $\hat{a}$ 为中心的 $n$ 维超椭球体， ${\chi }^2$ 与 $Q_a^{-1}$ 分别控制其大小和形状。其中，假设各个模糊度之间互不相关， $Q_{\hat{a}}$ 为对角阵，此时搜索域所表示的椭球退化为球体。只需对 $\hat{a}$ 就近取整即为固定解 $\hat{a}$ 。但在动态定位或快速定位的应用中，较短的观测时间及双差观测模式使得各模糊度间高度相关， $Q_{\hat{a}}$ 远非对角阵，此时搜索椭球被拉的很长。搜索过程异常复杂。

由于在利用最小二乘法进行整周模糊度解算过程中，各模糊度间高度相关所导致的搜索椭圆过于狭长，不利于整周模糊度的解算。可以使用一定的方法来降低模糊度组之间的相关性 [8] 。修正搜索范围，减少多余的误差解。其基本原理如下：

寻找一个 $Z$ 矩阵 [9] 满足：① $Z$ 中所有元素为整数；② det (Z) = ± 1；③ 可逆的整数变换，即变换前后参数的整数特性保持不变。变换后参数的协因数阵尽量接近对角阵。

对原始模糊度进行如下变换：

$z=Za$ ， $\hat{z}=Z\hat{a}$ ， $Q_{\hat{z}}=Z{Q}_{\hat{a}}{Z}^T$ (4)

${\left(\hat{z}-z\right)}^T{Q}_{\hat{z}}^{-1}\left(\hat{z}-z\right)\le {\chi }^2$ (5)

搜索使目标函数达到最小的 $z$ ，作为变换后的模糊度的固定解 $\hat{z}$

反变换得到原始模糊度的固定解。

3. 长短基线法算法原理

在短基线模型中，接收机 $r_i$ 和接收机 $r_0$ 到卫星 $s$ 的单位视线向量 [10] 认为是相同的，都记为 $e^s$ 。单差模型的几何示意图如图1所示。

根据几何关系，接收机 $r_i$ 和接收机 $r_0$ 到卫星s的几何距离单差值可以表示为 ${\rho }_{r_i{r}_0}^s=-e^s{b}_i$ ，因此载波相位单差方程可以写成下式 [11] ：

即：

${\varphi }_{r_i{r}_0}^s=\frac{-e^s{b}_i}{\lambda }+N_{r_i{r}_0}^s\text{+}{\epsilon }_{\varphi ,r_i{r}_0}^s$ (5)

式中， ${\varphi }_{r_i{r}_0}^s={\varphi }_{r_i}^s-{\varphi }_{r_0}^s$ ， ${\rho }_{r_i{r}_0}^s\text{=}{\rho }_{r_i}^s-{\rho }_{r_0}^s$ ， $N_{r_i{r}_0}^s=N_{r_i}^s-N_{r_0}^s$ ， ${\epsilon }_{\varphi ,r_i{r}_0}^s$ 为载波相位单差噪声， $\lambda$ 为载波波长。 ${\rho }_r^s$ 为接收机r天线相位中心和卫星s天线相位中心之间的几何距离， $N_r^s$ 为接收机r和卫星s之间测量的载波相位整周模糊度， ${\epsilon }_{\varphi ,r}^s$ 为载波相位测量误差。

1) 第一条短基线测姿方法 [12]

第一条基线矢量 $b_1$ 的长度小于半个载波波长，我们称之为超短基线。第一条基线由天线 $A_0$ 和天线 $A_1$ 组成，天线 $A_1$ 和 $A_0$ 的距离 $d_1$ 应该满足小于半波长：

忽略观测误差，式(5)可以转化为： ${\varphi }_{r_1{r}_0}^s=\frac{-e^s{b}_1}{\lambda }+N_{r_1{r}_0}^s$ ，根据预先设置的小于半波长基线向量 $b_1$ 及 $\left|e^s\right|<1$ 可以获得 $\left|\frac{e^s{b}_1}{\lambda }\right|<\frac{1}{2}$ ，即第一条基线的载波相位方程右侧的第一项必定是小数。 $N_{r_1{r}_0}^s$ 为整数。所以载波相位单差值可以分解成整数部分和小数部分。整数部分 ${\varphi }_{r_1{r}_0,\mathrm{int}}^s$ 和小数部分 ${\varphi }_{r_1{r}_0,frac}^s$ 分别为：

$\begin{array}{l}{\varphi }_{r_1{r}_0,\mathrm{int}}^s=round\left({\varphi }_{r_1{r}_0}^s\right)=N_{r_1{r}_0}^s\\ {\varphi }_{r_1{r}_0,frac}^s=frac\left({\varphi }_{r_1{r}_0}^s\right)=\frac{-e^s{b}_1}{\lambda }\end{array}$ (60

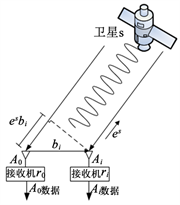
Figure 1. Geometric schematic diagram of single difference model between receivers

图1. 接收机之间的单差模型几何示意图

其中， $round(\cdot )$ 表示四舍五入取整， $frac(\cdot )$ 表示四舍五入取整之后的小数残留。

从数学模型推导可知，假如可见卫星个数为m，那么使用最小二乘算法，就可以求解出基线矢量 $b_1$ ：

$b_1={\left(H_1^T{H}_1\right)}^{-1}{H}_1^T{y}_1$ (7)

其中， $y_1={\left({\varphi }_{r_1{r}_0,frac}^1,{\varphi }_{r_1{r}_0,frac}^2,\cdots ,{\varphi }_{r_1{r}_0,frac}^m\right)}^T$ ， $H_1=\frac{-1}{\lambda }{\left(e^{1,T},e^{2,T},\cdots ,e^{m,T}\right)}^T$ 。

求解出基线矢量 $b_1$ 后，可以求解出基线的仰角 ${\theta }_1$ 和方位角 ${\phi }_1$ 。

2) 第二条基线测姿方法

如果已知第一条基线矢量 $b_1$ 确定的姿态(仰角 ${\theta }_1$ 和方位角 ${\phi }_1$ )，那么可以通过基线矢量和姿态角的关系估计出第二条基线矢量 $b_2$ 在当地ENU坐标系 [13] 中的粗略值：

${\hat{b}}_2\text{=}\left[\begin{array}{c}{\hat{b}}_{2,e}\\ {\hat{b}}_{2,n}\\ {\hat{b}}_{2,u}\end{array}\right]\text{=}\left[\begin{array}{c}{d}_2\cos \left({\theta }_1\right)sin\left({\phi }_1\right)\\ d_2\cos \left({\theta }_1\right)cos\left({\phi }_1\right)\\ d_2\sin \left({\theta }_1\right)\end{array}\right]$ (8)

之后，根据载波相位单差方程可以求出 $A_2$ 和 $A_0$ 的单差整周模糊度估计值为：

${\hat{N}}_{r_2{r}_0}^s={\varphi }_{r_2{r}_0}^s\text{+}\frac{e^s{\hat{b}}_2}{\lambda }$ (9)

为了使用第一条基线矢量 $b_1$ [14] ，快速确定天线 $A_2$ 和 $A_0$ 之间的单差整周模糊度 ${\hat{N}}_{r_2{r}_0}^s$ ， $A_2$ 和 $A_0$ 的距离应该满足估计的第二条基线矢量与真实摆放的第二条基线矢量差值的模小于半波长 [15] 。

通过对估计的整周模糊度 ${\hat{N}}_{r_2{r}_0}^s$ 进行四舍五入取整运算，就可以求出整周模糊度 ${\hat{N}}_{r_2{r}_0}^s$ 。

假如可见卫星个数为m，那么使用最小二乘算法，就可以求解出基线矢量 $b_2$ 。

$b_2={\left(H_2^T{H}_2\right)}^{-1}{H}_2^T{y}_2$ (10)

其中：

$y_2={\left[{\varphi }_{r_2{r}_0}^1-round\left({\hat{N}}_{r_2{r}_0}^1\right),{\varphi }_{r_2{r}_0}^2-round\left({\hat{N}}_{r_2{r}_0}^2\right),\cdots ,{\varphi }_{r_2{r}_0}^m-round\left({\hat{N}}_{r_2{r}_0}^m\right)\right]}^T$ ，

$H_2=\frac{-1}{\lambda }{\left(e^{1,T},e^{2,T},\cdots ,e^{m,T}\right)}^T$ (11)

求解出基线矢量 $b_2$ 后，根据基线矢量和姿态角 [16] 的关系，可以求解出基线的仰角 ${\theta }_2$ 和方位角 ${\phi }_2$ 。

对于布局为直线阵列形式的M个天线(分别记为 $A_0,A_1,\cdots ,A_{M-1}$ )按照特殊的几何配置要求，摆放成直线阵列形式，如图2所示。

以天线 $A_0$ 作为参考天线，天线 $A_0$ 到天线 $A_i$ 的基线矢量称为第i条基线矢量，记为 $b_i$ 。天线 $A_0$ 到天线 $A_i$ 的距离记为 $d_i$ ，那么有 $\left|b_i\right|\text{=}{d}_i$ 。其中 $i=1,2,\cdots ,M-1$ 。这些天线所连接的接收机(分别记为 $r_0,r_1,\cdots ,r_{M-1}$ )通过同一个晶体振荡器完成时间的同步。

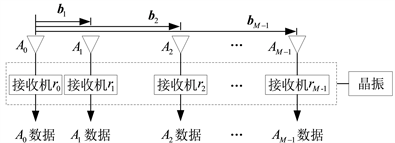
Figure 2. Schematic diagram of receiver antenna model

图2. 接收机天线模型示意图

由于超短基线解算的模糊度 [17] 精确度不高，不适宜作为载波相位解算的条件，可以利用求解第一条基线的方法处理短基线 $b_1$ ，然后在用第二条基线求解方法来处理基线 $b_2$ ，可以大大的降低误差。如果条件允许，可以继续利用相同的方法来处理基线 $b_2$ 和 $b_3$ ，能够获得更加精确的模糊度数。但是实际应用中，飞行器的空间有限，并不支持很多根共线的天线同时使用。一般使用两条基线来完成整周模糊度的解算。

4. 仿真分析

4.1. 仿真条件设计

已知GPS卫星L1信号的波长为0.192 m，所以，短基线的长度必须满足 $l_1<\frac{\lambda }{2}$ ，即 $l_1<0.096$ ，取短

基线长度为0.09 m，而对于长基线来说，只要是短基线的倍数即可。为了计算方便，取长基线是短基线的20倍，即 $l_2=1.8\text{m}$ 。选取6颗卫星进行载波相位观测并对长短基线法与LAMBDA算法的可靠性进行分析。为了判断LAMBDA算法与长短基线法之间的区别，每50个历元90度旋转一次天线。并利用六颗卫星对天线进行载波量为观测，获得相应的载波相位观测方程。

4.2. 仿真结果分析

图3中反应的是载波相位整周模糊度解算过程中长短基线法与LAMBDA算法的解算结果。

在载波相位观测过程中的整周模糊度解算算法上，忽略基线向量长度的约束，根据利用式(1)可以解算出载波相位整周模糊度的浮点解。但是，由于整周模糊度的值含有整周特性，就需要构建一个整数的搜索范围。然后在这个搜索的范围内，将所有的可行的解算结果计算出来。由于搜索过程中包含有最小二乘解算过程中获得协方差矩阵，而在单一历元的情况下，无法完成搜索域的构建。所以在使用LAMBDA算法时，必须利用多个历元的载波相位信息才能完成解算过程。并且模糊度维数越大，完成解算所需要的历元就越多。

对于同一个载体上的两条共线的基线向量，其相对载体的姿态角都是相等的。两个基线向量之间相差的倍数即为基线长度的之间的倍数。将短基线进行相应的设计，使观测出的载波相位值的小数部分与基线长度有关，通过短基线接收到的载波相位信息估计出基线向量，利用基线向量的倍数关系获得估计的长基线矢量，再利用估计出的矢量来完成整周模糊度的解算。短基线接收机每个历元都会接收到相应的载波相位信息，就可以通过获得信息获取每个历元中估计出的基线向量信息来完成后续的整周模糊度的解算，可以在任意一个历元获得所对应发整周模糊度。相对于LAMBDA算法，长短基线法有较强的时效性。使用与算法的快速解算上。

但是，对于长短基线法来说，结果的准确度与短基线解算出的短基线矢量有很大的关联，如果短基线的解算出现了较大误差甚至于错误将会在结果中引入更大的错误。

短基线向量的求解方式为：

$b_1={\left(H_1^T{H}_1\right)}^{-1}{H}_1^T{y}_1$ (12)

其中 $$ ，一般情况下矩阵 $H_1$ 中的方向向量 $e^{m,T}\ne \text{0}$ ，即卫星不在基准站的正上方。

通过短基线的载波相位观测值可以较好的获得载体的仰角和方位角。但是，当基准站与卫星信号发射的方向垂直时，此时的方向向量 $e^{m,T}\text{=0}$ ， $H_1^T{H}_1$ 的对角线上就出现了0元素，在计算机中 ${\left(H_1^T{H}_1\right)}^{-1}$ 就会产生严重放大的问题，此时，导致原本不变的姿态角出现了较大的变化，此时继续使用求解出的姿态角解算出的模糊度就会出现较大的误差。

对于长短基线法来说，短基线的极限矢量求解过程中的系数随着视线向量不断变化，导致估计的方位角是一个动态变化的过程，但是在相邻历元的变化较小可以忽略不计。所以图3中整周模糊度解算结果的精确度几乎没有差距。但是，当历元到达80时，长短基线法的结果相对LAMBDA算法就出现较大的误差甚至于是错误。通过图4可以看出，在第80历元之后，短基线所求解的姿态角出现了明显的跳变。此时的卫星与接收机的视向量垂直于基线，即 $e^{m,T}\text{=0}$ ，此时最小二乘法求解短基线向量的系数

$H_1=\frac{-1}{\lambda }{\left(e^{1,T},e^{2,T},\cdots ,e^{m,T}\right)}^T$ 出现0元素，计算机中 ${\left(H_1^T{H}_1\right)}^{-1}$ 0元素的求逆就会带来缩放的错误，从而导致解算结果出现错误。到了250历元时，方位角角度回到正确的水平，解算的结果也回到正确的水平。

Figure 3. Results of integer ambiguity resolution

图3. 标整周模糊度解算结果

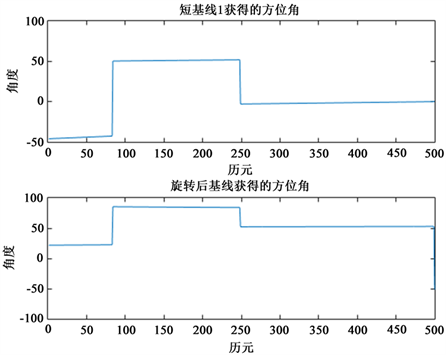
Figure 4. The change of short baseline attitude angle in the process of calculation

图4. 解算过程中短基线姿态角变化

5. 总结

在利用载波相位观测进行导航定位的过程中，载波相位的结果的准确度影响解算的最终结果。本文较为详细的阐述了整周模糊度解算的两种算法原理。并通过对长短基线法以及LAMBDA算法进行整周模糊度解算过程进行仿真。通过结果可以发现长短基线法能在一定的程度上提高解算的效率。但是当天线与卫星之间的夹角在一定的范围内时，将会导致解算的结果出现较大的误差。影响整周模糊度解算的正确性。而这个影响需要进行进一步的研究和仿真模拟。