1. 引言
多属性群决策 [1] [2] [3] [4] 是指多个专家针对具有多个属性的有限个方案进行排序和选择的一类决策问题。目前,有关将三角模糊集应用到多属性决策方面的研究已经成了众多学者研究的主题,但是,随着社会问题的日益复杂化和科学技术的不断发展,单个决策者很难考虑到决策问题的方方面面,为了保证决策过程的科学性和合理性,在决策过程中需要包含多个决策者。目前,针对三角模糊数多属性群决策问题的研究已经取得了不错的进展 [5] - [11] 。杨雷,漆国怀 [5] 通过借鉴集对分析理论和统计学理论的思想,将区间三角模糊数转化为“均值 + 方差”二元联系数的形式,进一步提出了一种基于集对分析二元联系数的决策方法。基于此,研究了属性值和属性权重均为区间三角模糊数的多属性群决策问题。Shi-fang Zhang,San-yang Liu,Renhe Zhai [6] 为了确定准则权重,建立了基于传统GRA方法基本思想的优化模型,给出了MCDM扩展GRA方法的计算步骤,进一步提出了一种准则权重信息完全未知情形下的基于区间值三角模糊数求解MCDM问题的扩展灰色关联分析(GRA)方法。张市芳 [7] 利用给出的动态区间三角模糊加权平均(DITFWA)算子对各时段的平均值进行集成,进一步提出了一种在各决策时段的时间权重已知的情况下,基于区间三角模糊数的动态多属性群决策问题。Huimin Zhang [8] 通过定义集成算子和得分函数,进一步对区间值二型模糊数的决策问题进行了研究。Ashtiani B.,Haghighirad F.,Makui A.,Montazer G. A. [9] 在属性权重完全已知的情形下,提出了一种基于TOPSIS的区间三角模糊数决策方法。Vahdani B.,Hadipour H.,Sadaghiani J. S.,Amiri M. [10] 提出了一种属性权重完全已知的基于VIKOR的区间三角模糊数决策方法。要瑞璞,沈惠璋 [11] 定义了区间值三角模糊数几何加权均值((ITFGWM)算子。并对Caxlsson定义的均值进行扩展,从而给出了区间值三角模糊数的均值定义。进而提出了一种基于区间值三角模糊数的模糊多属性群决策的方法,最后给出一个实例进行分析。
Hwang和Yoon于1981年提出了TOPSIS方法 [12] ,并且被广泛地研究与应用,在TOPSIS方法中,一个理想方案的选择应该在接近正理想方案的同时远离负理想方案。Yang Wei等提出了一种用TOPSIS [13] [14] 确定专家权重的新方法,不过其中决策者给出的评价值是以直觉模糊数的形式给出的,这样对于处理决策过程中的模糊性和不确定性有一定的弊端。因此,在本文中,我们对上述方法进行了改进,在决策者的评价值是以区间三角模糊数给出的情况下,给出了一种用TOPSIS确定专家权重的一种新方法。该方法更有利于考虑到决策过程中的模糊性和不确定性,而且适用于方案集和属性集非常大的情况。为了将不同的决策者给出的评价值集结为一个,我们首先定义了区间三角模糊正,负理想矩阵,然后计算每个评价值到区间三角模糊正,负理想矩阵之间的距离,接着我们通过计算得到了每个评价值的贴近度,进一步求得了专家权重。通过我们的方法确定的权重有两个优势:第一如果评价值接近正理想点并且同时远离负理想点就会被赋予一个较高的权重;否则,评价值就会被赋予一个小的权重;第二,降低了过高或过低的评价值对排序结果的影响。并且考虑了不同属性权重信息的情况:属性权重完全已知,部分已知和完全未知。如果属性权重完全已知,在将不同的决策者给出的评价值集结为一个之后,我们用TOPSIS方法对决策结果进行排序;如果属性权重部分已知,我们通过求解一个线性规划模型来求得属性权重;如果属性权重完全未知,我们同样用TOPSIS方法得到属性权重。最后我们提出了一种与之相一致的算法,并且通过一个实例证明了该方法的有效性。
在下文中,我们首先给出了有关区间三角模糊集的基本概念;在第二部分,我们给出了一种基于TOPSIS的确定专家权重的新方法;同时考虑了属性权重在不同情况下的情形;在第三部分,我们用一个实例证明了该算法的有效性和可行性;在第四部分,给出了结论。
2. 区间三角模糊集基本理论
定义1 [9] :若
,其中
,则称
为一个区间三角模糊数,也可以记作
。
下面给出两个区间三角模糊数之间的运算法则:
定义2 [9] [15] :设任意两个区间三角模糊数
和
,
为任意的正实数,则有:
1)
;
2)
。
定义3 [11] :设
为一个区间三角模糊数,定义其上界均值
和下界均值
分别为:
(1)
(2)
其中: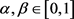 ,由此得出区间三角模糊数
的区间均值为
。
,由此得出区间三角模糊数
的区间均值为
。
定义4 [11] :设任意两个区间三角模糊数
和
,均值分别为
,
,则称
(3)
为
的可能度。
对于上述定义的可能度,易证明以下结论成立。
1)
;
2)
,当且仅当
;
3)
,当且仅当
。
定义5 [7] :设任意两个区间三角模糊数
和
,则
和
的Hamming距离为
(4)
3. 一个新的区间三角模糊集多属性群决策方法
假定一个多属性群决策问题由以下条件给出:设
为专家集,
为方案集,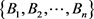 为属性集。决策者
给出方案
相对于属性
的评价值
,
,进一步构成区间三角模糊数决策矩阵:
为属性集。决策者
给出方案
相对于属性
的评价值
,
,进一步构成区间三角模糊数决策矩阵:
(5)
在决策方法中,应该首先将不同的决策矩阵归一化。基于TOPSIS方法,为了避免过高或过低的评价值对排序结果的影响,接近正理想点且同时远离负理想点的评价值应该被赋予较高的权重,否则评价值就应该被赋予一个较小的权重。因此平均评价值就可以看作是区间三角模糊正理想评价值。定义区间三角模糊正理想矩阵。
定义6:区间三角模糊正理想矩阵为
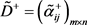 (6)
(6)
其中
,
。
定义7:区间三角模糊负理想矩阵能够被分成
和
两个部分:
(7)
(8)
其中
,
。
和
,
,
之间的距离定义如下:
(9)
(10)
(11)
的贴近度为:
(12)
方案
相对于属性
的决策者
的权重由以下公式给出:
(13)
其中
。
不同的决策者给出的评价值可以利用
(14)
集结成综合评价值
构成决策矩阵
(15)
在决策过程中,经常会遇到属性权重信息是部分已知的情况,一般地,部分已知的属性权重信息可以由如下集合表示 [16] [17] :
1)
;2)
;
3)
;
4)
;
5)
。
为了确定属性的权重信息,首先定义区间三角模糊正理想解
(16)
和区间三角模糊负理想解
(17)
根据
到其正负理想解的距离集结每个评价值计算贴近度如下:
(18)
进一步可得加权贴近度:
(19)
一个理想权重的选择应使贴近度尽可能大,建立多目标优化模型,记为
因各方案是同等重要的,上述多目标优化模型可由单目标优化模型代替,记为
某些情况属性权重是完全未知的,在这种情况下,根据以下原则来确定属性的权重:属性的集结评价值接近区间直觉模糊正理想解,同时远离区间直觉模糊负理想解时应该被赋予一个较大的权重。据此,属性权重可以由如下公式得出:
(20)
下面我们给出基于新权重方法的一个区间直觉模糊集多属性群决策方法。
步骤1:决策者
给出方案
相对于属性
的评价值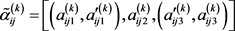 ,
,进一步构成:决策矩阵:
。
,
,进一步构成:决策矩阵:
。
步骤2:根据式子(6),(7)和(8)计算区间三角模糊正理想决策矩阵
和区间三角模糊负理想决策矩阵
,
。
步骤3:根据式子(9),(10),(11)和(12)计算每个评价值的贴近度。
步骤4:如果属性权重完全已知,直接进行步骤5,如果属性权重部分已知,则用
计算出属性权重,如果属性权重完全未知,则用式子(20)计算出属性权重。
步骤5:计算加权决策矩阵
其中
。
是属性权重的集合。
步骤6:由以下公式计算
与区间三角模糊正负理想解之间的距离:
(21)
(22)
步骤7:计算每个方案的相对贴近度
(23)
步骤8:根据相对贴近度的大小对方案进行排序并选出最优方案。
4. 算法实例
某个风险投资公司想要进行高科技项目投资问题,有四个备选企业可供选择,分别为
。经过研究制定了四项评估指标:管理能力(B1),生产能力(B2),风险承担能力(B3)和企业战略一致性(B4)。将三位决策者给出的评价信息经过处理后得到了区间三角模糊决策矩阵,
。如表1,表2,表3所示。在属性权重信息分别为:属性权重完全已知,部分已知,完全未知的情况下,我们用上述算法选出最优投资项目。
步骤1:决策者给出方案关于属性的评价值构成区间三角模糊决策矩阵
。如表1,表2,表3所示。
步骤2:根据式子(6),(7)和(8)计算区间三角模糊正理想决策矩阵
和区间三角模糊负理想决策矩阵
,
。如表4,表5,表6所示。
步骤3:对于每个决策者
,计算每个评价值
到正理想评价值
与负理想评价值
,
之间的距离。然后根据公式(12)计算贴近度,根据公式(13)计算专家权重。然后利用公式(14)将不同决策者给出的评价值集结成综合评价值,构成决策矩阵D。如表7所示。
步骤4和5:若已知的属性权重信息为
计算加权决策矩阵
,
计算结果如表8所示。
步骤6:计算每个方案的综合评价值与其区间三角模糊正理想解
和区间三角模糊负理想解
之间的距离,分别用
表示。
步骤7:根据式子(23)计算每个方案的相对贴近度,步骤6和步骤7的计算结果如表9所示。
步骤8:根据相对贴近度的大小对方案进行排序并选出最优方案。
最优投资项目为:
。
在上述例子中,不同决策者对于不同评价值的权重是不同的。并且通过这个方法确定的权重能够减少过高或过低的评价值对排序结果的影响。为了证明该方法的优越性,我们将该方法与专家权重预先给出的情况进行比较。例如,专家权重为(0.2, 0.3, 0.5)由(13)将不同决策者给出的评价值集结成综合评价值构成决策矩阵。如表10所示。
若已知属性权重信息为
则计算加权决策矩阵
,
如表11所示。进一步我可以计算得到每个方案的相对贴近度,如表12所示。

Table 1. Interval-triangular fuzzy decision matrix D ( 1 )
表1. 区间三角模糊决策矩阵

Table 2. Interval-triangular fuzzy decision matrix D ( 2 )
表2. 区间三角模糊决策矩阵

Table 3. Interval-triangular fuzzy decision matrix D ( 3 )
表3. 区间三角模糊决策矩阵

Table 4. Interval-triangular fuzzy positive ideal decision matrix D +
表4. 区间三角模糊正理想决策矩阵

Table 5. Interval-triangular fuzzy negative ideal decision matrix D u
表5. 区间三角模糊负理想决策矩阵

Table 6. Interval-triangular fuzzy negative ideal decision matrix D d
表6. 区间三角模糊负理想决策矩阵

Table 7. Interval-triangualr fuzzy collective decision matrix D
表7. 区间三角模糊集结决策矩阵D

Table 8. Interval-triangular fuzzy weighted decision matrix D ′
表8. 区间三角模糊加权决策矩阵

Table 9. The closeness coefficient of each alternative with unknown export weight
表9. 专家权重未知情况下每个方案的相对贴近度

Table 10. Interval-triangualr fuzzy collective decision matrix D ( 1 )
表10. 区间三角模糊集集结决策矩阵

Table 11. Interval-triangular fuzzy weighted decision matrix D ′ ( 1 )
表11. 区间三角模糊集加权决策矩阵

Table 12. The closeness coefficient of each alternative with known export weight
表12. 专家权重预先给出情况下每个方案的相对贴近度
根据贴近度大小进行排序:
,最优投资项目为:
以上排序结果和用刚刚的算法得到的排序结果是不同的,在这种情况下,决策者对于所有属性的权重是相同的,但是在实际的决策问题中,由于决策问题的复杂性,就需要更多的知识来解决决策问题。由于专家很可能对一些属性熟悉而对另一些不熟悉,这就促使他们对一些属性给出合理的评价值,同时对其它属性给出不合理的。将该算法和现有的方法进行比较,可以发现,该算法能够降低过高或过低的评价值对于排序结果的影响。
对于权重信息部分已知的情况,往往先构建一个单目标线性规划模型,再按如下步骤对方案进行排序。设已知的部分权重信息为:
构建单目标线性规划模型
求解该模型,我们可以得到属性的权重向量(0.23, 0.26, 0.18, 0.33)进一步,可以计算得到加权决策矩阵
计算结果如表13所示。接着可以求出每个方案的相对贴近度,如表14所示。然后可以根据相对贴近度的大小对方案进行排序。
如果属性权重完全未知时,可以根据相对贴近度的大小对方案进行排序。
先根据式子(18)计算
的贴近度
如表15所示,再根据式子(20)计算属性权重得(0.394, 0.190, 0.134, 0.282)。进一步可以得到加权决策矩阵,如表16所示。接着可以计算得到每个方案的相对贴近度,计算结果如表17所示。

Table 13. Interval-triangular fuzzy weighted decision matrix D ′ ( 2 )
表13. 区间三角模糊集加权决策矩阵

Table 14. The closeness coefficient of each alternative with partly known weight information
表14. 部分权重信息情况下每个方案的相对贴近度
根据贴近度大小进行排序:
最优投资项目为:
。

Table 15. The coefficient c i j of α i j
表15.
贴近度

Table 16. Interval-triangular fuzzy weighted decision matrix D ′ ( 3 )
表16. 区间三角模糊集加权决策矩阵

Table 17. The closeness coefficient of each alternative with completely unknown. weight information
表17. 每个方案的相对贴近度
根据贴近度大小进行排序:
,最优投资项目为:
。
5. 结束语
本文给出了一个基于TOPSIS的区间三角模糊集群决策方法,在本文中,由不同决策者给出的评价值的权重是由TOPSIS方法确定的,这种新的权重确定方法能够减少过高或过低的评价值对排序结果的影响。对于属性权重,本文考虑到了不同情形下的属性权重。如果属性权重部分已知,可以通过求解一个线性规划模型来得到属性权重;如果属性权重完全未知,可以根据以下原则来确定属性权重:接近正理想点同时远离负理想点的属性应该被赋予一个较大的权重,否则就应该被赋予一个较小的权重。最后通过一个实例证明了该方法的可行性和有效性。
基金项目
陕西省社会科学基金项目13D175。