基于EMD的北京与天津PM2.5相关结构探究

Study on Correlation Structures between Beijing and Tianjin PM2.5 Based on EMD

摘要: 为了深入探究北京市与天津市空气质量的相关性，通过计算相关系数矩阵，分别找出了两地最具代表性的空气质量指标均为PM2.5，利用经验模态分解(EMD)对北京市PM2.5和天津市PM2.5时间序列进行模态分解，基于周期进行模态重构，借助互相关函数对重构后的模态组合进行动态相关性分析。结果表明：北京市PM2.5和天津市PM2.5在趋势项上高度相关，高频部分之间强相关，在PM2.5的低频部分北京市滞后于天津市，且滞后1天时两序列达到最大正相关。

Abstract: In order to explore the correlation between air quality in Beijing and Tianjin, the most representative air quality indexes in Beijing and Tianjin were found to be PM2.5 by calculating the correlation coefficient matrix. Empirical mode decomposition (EMD) was used to decompose the PM2.5 time series in Beijing and Tianjin, and modal reconstruction was carried out based on the period. The results show that PM2.5 in Beijing and PM2.5 in Tianjin are highly correlated in trend terms and strongly correlated in high-frequency parts. In the low-frequency part of PM2.5, Beijing lags behind Tianjin, and the two sequences reach the maximum positive correlation when lagging 1 day.

1. 引言

自20世纪30年代以来，美国、英国、日本等不同国家的城市相继发生了轰动世界的8大公害事件，其中有5件都是空气污染引发，给城市安全及居民健康、城市的可持续发展均带来了负面的影响。因此，空气质量问题严重制约国家城市可持续发展战略，也愈来愈引起政府和社会各界的广泛关注。而北京作为我国政治、经济、文化中心，其空气质量就更是大众较为关心的焦点问题，首当其冲成为众多学者讨论和研究的主要对象。同时，在我国大力推进生态文明建设的背景下，空气污染已经成为北京市全面建成小康社会的短板问题。而随着社会经济发展水平的进一步提高，北京市居民对良好空气质量的需求愈发强烈。为了改善北京空气质量，仅从行政区划的角度考虑单个城市雾霾污染防治的“各自为战”的环境管理和污染治理模式已经难以有效解决当前愈加严重的区域雾霾污染问题，加强区域联防联控以形成跨区域协同治污合力势在必行。天津市位于华北平原东北部，东临渤海，北依燕山，人口密集，工商业发达，是北方重要的交通枢纽和最大的沿海开放城市，位于北京市东南方向约110千米，与北京同处于一个大气流场，并且两地常年盛行两个风场辐合带，也就是污染物汇聚带，一条是沿豫北–冀中南–北京–冀北沿线的风场辐合带，另一条是鲁西南–冀东–天津–冀北沿线的风场辐合带，在两条辐合带的影响下，该地区间污染物相互输送，互相影响，形成区域大气复合污染 [1] 。同时，天津作为仅次于北京的特大城市，高密度的人口，显著增长的机动车保有量，导致天津的污染也相当严重。在此背景下，深入探究北京市空气污染与天津空气污染之间的相关结构，对于完善雾霾污染的跨区域协同治理机制具有重要的理论价值和现实意义。

目前，已有较多文献对北京的空气质量进行综合特征分析，及其影响因素研究，其中，张森2017年利用全局空间相关性理论，得出京津冀13个城市的空气污染呈现出显著的空间相关性 [2] ；马丽梅、张晓2014年利用局部空间相关性理论，发现北京、天津、河北、山西、山东、河南、黑龙江、吉林、辽宁之间存在高–高类型的集聚 [3] ，同时，在区域大气污染空间效应的研究中发现：相邻地区的影响是造成北京市PM10较高的重要原因之一 [4] 。为了探究周边城市对北京空气质量的影响，多数文献采用大气数值模拟方法研究污染物的输送规律，并计算北京市污染物内外源的贡献率，例如，Streets运用CMAQ模式分析了北京市奥运会期间颗粒物和臭氧的来源，得出周边城市对北京大气污染物浓度的贡献率 [5] ；王郭臣、王东启运用潜在源贡献因子分析法和浓度权重轨迹分析法，模拟了北京冬季严重污染过程的PM2.5输送路径和主要潜在源区 [6] 等。但是所有上述文献的研究均是对原始数据进行分析，未考虑数据信号本身包含信息的多样性和复杂性，经验模态分解(Empirical Mode Decomposition，简称EMD)是一种处理非线性、非平稳信号的视频分析方法，该方法依据输入信号自身的特点，自适应地将信号分解成若干个本征模态函数(Intrinsic Mode Function，简称IMF)之和 [7] 。EMD被认为是对以线性和平稳假设为基础的傅里叶分析和小波变换等传统视频分析方法的重大突破 [8] 。

本文从时间序列的角度引入一个新的方法，结合EMD将北京市与天津市空气质量信号分解为有限个IMF分量，其中每个IMF包含原信号不同时间尺度的局部特征信号，进而从不同时间尺度对北京市与天津市空气质量的相关结构进行深入探究。本文的空气质量原始数据包括AQI、PM2.5、PM10、SO₂、CO、NO₂、O₃共7个空气质量指标，基于R软件分别计算北京和天津两地七个空气质量指标的相关系数矩阵，北京市与天津市的各个空气质量指标中与AQI相关性由强到弱依次均为PM2.5，PM10，CO等，其中北京市与天津市PM2.5与AQI的相关性分别高达0.947与0.943，进一步计算北京市与天津市PM2.5时间序列相关性系数达到0.76，从统计学的角度进行皮尔逊相关性检验，P值大于0.05，即通过了相关性检验，说明北京市PM2.5与天津PM2.5之间显著相关。同时已有文献得出PM2.5已经成为北京市空气中的首要污染物的结论，故本文将PM2.5作为北京市和天津市的首要污染物进行后续研究。为了从动态的角度分析两者的相关性，与求两个时间序列之间的相关系数不同，本文引入互相关函数的方法，来描述天津市与北京市PM2.5在任意两个不同时刻取值之间的相关程度。另外，相对于常规的大气数值模式，采用大气自动化监测数据是长期的，因为其考虑了污染的滞后及其累积效应，从而能更好地为城市自身减排和加强区域大气污染联防联治提供数据支持。

2. 数据与方法

2.1. 数据来源

本文数据来自https://www.aqistudy.cn/historydata/daydata，记录了2013年12月至今全国主要城市的历史天气，本文选取北京市和天津市从2014年1月1日至2017年12月12日的历史空气质量作为研究对象，组成两大时间序列，每组样本含有1461个数据，其中每大组时间序列包括AQI、PM2.5、PM10、SO₂、CO、NO₂、O₃共7个空气质量指标。

2.2. 研究方法

2.2.1. EMD分解

经验模态分解法是 N. E. Huang等人为了研究海浪在1998年提出来的一种适用于分析非线性、非平稳的信号序列的方法，它可以把复杂信号分解为有限个固有模态函数，分解后得到的各阶IMF都包含了原始信号中不同时间尺度下的局部特征信号。其中，第一个固有模态函数的振荡频率最高，其余的IMF震荡频率逐步衰减。所有的IMF满足以下两个条件：第一，极点的数量和零点的数量最多相差一个；第二，在任意点处上下包络的平均值为零。经验模态方法的算法大致如下 [9] ：

1) 对于给定的时间序列 $x\left(t\right)$ 找到其局部极大值 $e_{\max }\left(t\right)$ 和局部极小值 $e_{\min }\left(t\right)$ ，构造上包络和下包络，分别用三次样条局部极大值和局部极小值算法；

2) 估计两个包络的平均值 $M_1\left(t\right)=\frac{e_{\max }\left(t\right)+e_{\min }\left(t\right)}{2}$ ；

3) 令 $h_1\left(t\right)=x\left(t\right)-M_1\left(t\right)$ ，若 $h_1\left(t\right)$ 满足上述两个条件，则为第一个IMF (固有模态函数)，如果 $h_1\left(t\right)$ 不满足上述条件，将其作为新的时间序列重复以上步骤直到第k次，即 $h_{1k}\left(t\right)$ 为固有模态函数，则：

第一个固有模态函数为： $C_1\left(t\right)=h_{1k}\left(t\right)$ ；

第一个残余为： $r\left(t\right)=X\left(t\right)-C_1\left(t\right)$ ；

4) 一直重复前面步骤，直到 $r\left(t\right)$ 为单调函数或者常数，EMD分解结束.这样，原始信号 $X\left(t\right)$ 被分解成 $n-1$ 个固有模态函数和趋势项： $X\left(t\right)={\displaystyle {\sum }_{m=1}^{n-1}{C}_m\left(t\right)+r\left(t\right)}$ 。

2.2.2. 互相关函数

在信号处理中，互相关函数给出了在频域内两个信号是否相关的一个判断指标，把两测点之间信号的互谱与各自的自谱联系了起来。它能用来确定输出信号有多大程度来自输入信号，对修正测量中接入噪声源而产生的误差非常有效。本文对两个时间序列求互相关函数，可以反映出两个时间序列在不同的相对位置上互相匹配的程度 [10] 。

3. 分析与讨论

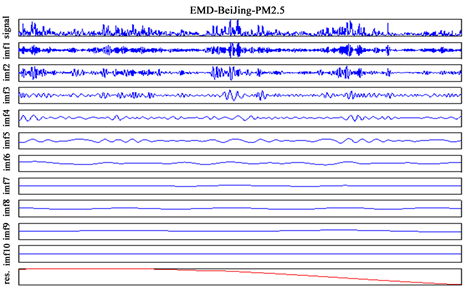
按照上节EMD算法，对北京市PM2.5序列和天津市PM2.5序列进行EMD分解，分别将北京市PM2.5时间序列分解成10个IMF分量和一个剩余分量，将天津市PM2.5时间序列分解成8个IMF分量和一个剩余分量，如图1(a)、(b)所示。

从图1的分解结果可以看出，分解出的各阶IMF从最高模态到最低模态的波动频率逐渐降低，波动周期越来越大.为了从不同时间尺度分析北京市PM2.5和天津市PM2.5的相关性，本文拟将北京市PM2.5和天津市PM2.5时间序列经EMD分解成的各个IMF分量和趋势项按一定的方法组合成三个部分，分别是高频部分、低频部分和趋势部分。通过图1可以看出分解出的各阶IMF模态越高，频率越高，故下一步需要确定选取哪几个较高模态作为高频部分。而基于EMD方法具有自适应性以及时间上的局部性这两个特点，在提取趋势和周期信息等方面有一定的优势，故对北京市PM2.5和天津市PM2.5 EMD分解后各IMF进行周期性分析，首先，对EMD分解后所得的各阶IMF计算得到极值点(极大值点和极小值点)的个数，记为N1；其次，采用平均周期法来计算各阶IMF的周期性，平均周期法的定义为：T = N/N1.其中的N为总体数据个数 [11] ，本文中N的值为1461；运用MATLAB软件计算所得结果见表1，表2，图2。

从表1可看出北京市PM2.5周期性变化非常明显.其中，IMF1周期为2天，可能是受气温、风速、气压等气象条件的影响，IMF2周期为3天，可能是受工业废气排放、燃煤和机动车尾气等大气污染物的影响，IMF3的周期为7天，大约为一周；IMF4的周期为13天，大约为半个月；IMF5的周期为29，约为一个月；此外，IMF7的周期为104天，大约为3个月，也就是一个季度，IMF10的周期为365天，大约为一年。由此可知，北京市PM2.5大体是按周、月、季度或年为周期进行变化的。同样地，从表2可看出天津市PM2.5周期性变化也非常明显.为了看清楚分解后各个IMF之间的关系，利用互相关函数计算北京PM2.5与天津PM2.5分解后各个IMF的相关系数，并进行皮尔逊相关性检验，结果见表3。

通过表3可以看出北京市PM2.5各个IMF与天津市PM2.5各个IMF之间都通过了皮尔逊相关性检验，通过图2北京市和天津市PM2.5的周期对比情况，可以看出，北京PM2.5与天津PM2.5进行EMD分解后前4个IMF具有相同的平均周期，说明这四个IMF分量背后代表的物理意义是一致的，且频率相对较高，故将北京市PM2.5时间序列分解后的IMF1~IMF4组合为高频部分，记为HS1，其余IMF组合为低频部分，记为LS1，趋势项记为TS1。同样地，天津市PM2.5时间序列分解后的IMF1~IMF4组合为高频部分，记为HS2，其余IMF组合为低频部分，记为LS2，趋势项记为TS2。这样就通过EMD分解将北京市PM2.5时间序列与天津市PM2.5时间序列分解为高频项，低频项和趋势项.之所以这样重构分解后序列，是因为三者代表了不同的信息，其中，高频部分代表较小因素对序列的影响，即该因素对时间序列时间的发生影响面积小，或者说影响持续时间较短；低频项反映了重大因素对序列的影响，是序列的重要组成部分，通常是序列产生剧烈波动的重要和主要因素；趋势项是序列的主要组成部分，代表序列的长期走势 [12] 。为了更直观的分析北京市PM2.5重构后的高频部分HS1与天津市PM2.5重构后的高频部分HS2之间的关系，做出其时序对比图见图3，低频部分LS1与LS2之间的时序对比图见图4。

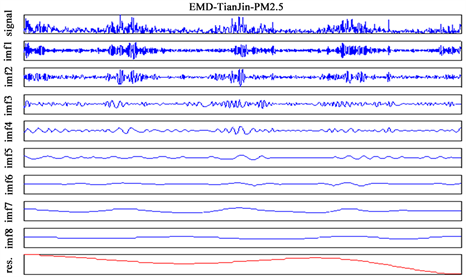(a) (b)

Figure 1. EMD diagram of Beijing PM2.5 and Tianjin PM2.5 time series. (a) EMD results of PM2.5 time series in Beijing; (b) EMD results of PM2.5 time series in Tianjin

图1. 北京市PM2.5、天津市PM2.5时间序列EMD分解图。(a) 北京市PM2.5时间序列EMD分解结果；(b) 天津市PM2.5时间序列EMD分解结果Table 1. IMF cycles of PM2.5 in Beijing表1. 北京市PM2.5各阶IMF周期

Table 1. IMF cycles of PM2.5 in Beijing

表1. 北京市PM2.5各阶IMF周期

Table 2. IMF cycles of PM2.5 in Tianjin

表2. PM2.5天津市各阶IMF周期

Table 3. IMF correlation and correlation test between Beijing and Tianjin PM2.5

表3. 北京市与天津市PM2.5各阶IMF相关性及相关性检验table_table_table_8-2580406_3_hanspub.htm

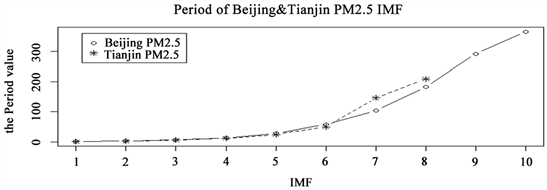
Figure 2. Comparison of IMF cycles of PM2.5 in Beijing and Tianjin

图2. 北京市与天津市PM2.5各阶IMF周期对比图

利用互相关函数计算重构后时间序列的动态相关性，见表4。通过上表可以看出，北京PM2.5与天津PM2.5重构后的时间序列高频项HS1与HS2之间滞后0天时，相关系数达到最大值0.74274，并通过了皮尔逊相关系数检验，说明其显著相关，并且其余滞后期对应的相关系数在0附近呈现周期性波动；天津PM2.5重构后的时间序列低频项LS1与北京PM2.5重构后的时间序列低频项LS2相关度达到0.6742，通过了皮尔逊相关系数检验，说明其显著相关，天津滞后北京1天时，相关系数达到最大值0.69792，并随着滞后天数的增加，相关系数逐渐减小，但在滞后10天时相关性仍然高于0.6，说明低频项之间呈现较强的相关性；天津PM2.5重构后的时间序列趋势项TS1与北京PM2.5重构后的时间序列趋势项TS2之间的相关性具有更明显的规律，在滞后期为0时相关性达到最强0.99502，随着滞后期的增加相关性单调递减为0。

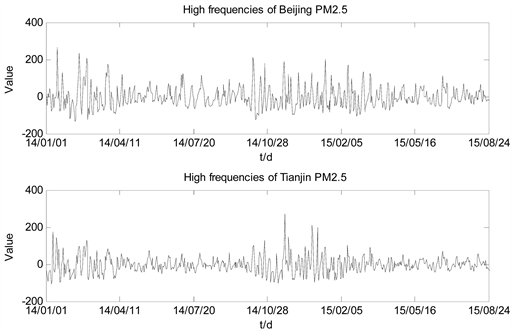
Figure 3. Comparison of PM2.5 high-frequency parts between Beijing and Tianjin

图3. 北京市与天津市PM2.5高频部分时序对比图

Figure 4. Comparison of PM2.5 low-frequency parts between Beijing and Tianjin

图4. 北京市与天津市PM2.5低频部分时序对比图

Table 4. Cross correlation results of reconstructed PM2.5 parts in Beijing and Tianjin

表4. 重构后北京市与天津市PM2.5各部分的互相关结果

4. 结论与讨论

本文利用EMD方法对北京市PM2.5时间序列和和天津市PM2.5时间序列分别进行多尺度分解，通过计算各个IMF分量的周期，将分解后序列重构为高频项，低频项和趋势项，研究发现北京市PM2.5序列和天津市PM2.5序列的趋势项高度相关，高频部分之间强相关，北京市PM2.5的低频部分滞后于天津市PM2.5的低频部分，利用互相关分析发现滞后1天时两序列低频部分达到最大的正相关。这表明北京市PM2.5与天津市PM2.5之间有较大的相关性。本文的研究创新主要体现在利用EMD方法创新性地将北京市PM2.5时间序列信号有意识地分解为长期波动信号和短期波动信号，因为一个时间序列不可能是只有一个因素造成，而不同的因素造成的序列波动特征应该是有差异的，因此将天津市PM2.5时间序列也做相应的分解，然后各个结构的相关性进行检验，这可能是挖掘北京市PM2.5和天津市PM2.5时间序列相关结构的可行方法。