基于VISSIM仿真的高速公路事故管控策略研究

Research on Expressway Accident Management and Control Strategy Based on VISSIM Simulation

摘要: 为了能够在高速公路发生交通事故后快速有效地减轻交通拥堵，本文利用收费站数据建立高速公路车辆速度模型，根据速度阈值判断某一路段是否发生交通事故，根据事故持续时间提出了一种基于VISSIM仿真的管控决策方法。选取“排队长度”参数作为管控方案的评价指标，通过对事故上游的收费站入口禁行时间和入口数量进行管控。以山东青临高速公路某一路段为例，VISSIM仿真和实际应用结果表明：车辆速度模型的使用及管控方案的实施，具备科学的辅助决策作用，为高速公路的实时性管控提供了强有力的技术支持。

Abstract: In order to reduce traffic congestion quickly and accurately after traffic accidents on express ways, in this paper, we use toll station data to establish freeway vehicle speed model. According to the speed threshold, we can judge whether there is a traffic accident on a certain road. According to the duration of accidents, a decision-making method of management and control based on VISSIM simulation is proposed. The “queue length” parameter is selected as the evaluation index of the management and control scheme, and the prohibition time and the number of entrances at the charging stations upstream of the accident are controlled. Taking a typical expressway section in Shandong Province as an example, the results of VISSIM simulation and practical application show that: the use of vehicle speed model and the implementation of management and control scheme have a scientific assistant decision-making role, and provide a strong technical support for the real-time management and control of expressway.

1. 引言

随着高速公路通车里程和汽车保有量的急剧增加，给人们生活带来方便的同时也增加了交通拥堵、交通事故的发生。由于交通事故带有偶发性、不可预测性的特点 [1] ，在实际研究中往往难以及时获取到交通事故的响应信息；同时，由于交通事故相关的历史数据具有不对外公开性，导致研究起来相当困难。当复杂的交通系统无法用简单抽象的数学模型描述时，交通仿真便成为研究交通问题的重要途径。对于事故路段通行能力的研究，美国学者Goolsby等最早研究了交通事故造成高速公路车道阻塞后的瓶颈路段通行能力，给出了不同紧急事件下高速公路有效通行能力的比例 [2] 。由于国内外高速公路车辆运行特性存在差异，为此，本文采用VISSIM仿真软件构建我国基于VISSIM的高速公路事故路段的仿真模型，采用青临高速公路车辆运行特征参数，介绍一种基于VISSIM仿真的高速公路管控方案。

2. 高速公路管控模型

2.1. 路段模型

基于高速路网拓扑，构建高速路交通状态判别模型。

以由南向北方向高速路段入口A、出口B之间的路段为研究对象。如图1所示，入口A和出口B之间的路段长度为L0。设统计时段为 $\left[t_{1,}{t}_2\right]$ ，时间差为 $\Delta t=t_2-t_1$ ，在此时间段内该高速路段的交通流量组成分为两类：第一类为由入口A进入且由出口B流出的交通流 $Q_{AB}$ ；第二类由经过路段L0的过境交通流 $Q_{AB}^1$ 、 $Q_{AB}^2$ 、……、 $Q_{AB}^n$ 组成，其中 $Q_{AB}^1$ 表示该支车流量经过路段AB且入口和出口之间有2个路段，以此类推， $Q_{AB}^n$ 表示该支车流量经过路段AB且入口和出口之间有n + 1个路段。

2.2. 速度模型

以当前计算路段的出入口交通流量对应的平均速度为主要依据，兼顾经过此路段的过境交通流量的平均速度，将其加权求和，得到本路段的平均速度。

Figure 1. Section model

图1. 路段模型

1) 根据前面条件设定，设待求AB区间的区间平均速度为 ${\bar{V}}_{AB}$ ，其计算公式如下：

${\bar{V}}_{AB}={\alpha }_1{\bar{v}}_{AB}+{\alpha }_2{\bar{v}}_{AB}^{\text{'}}$ (1)

其中， ${\bar{v}}_{AB}$ 为由AB口直接对应的车流平均速度； ${\bar{v}}_{AB}^{\text{'}}$ 为AB口的过境交通流对应的车流平均速度，权值 ${\alpha }_1$ 和 ${\alpha }_2$ 表示两车速平均值的重要程度( ${\alpha }_1>>{\alpha }_2且{\alpha }_1+{\alpha }_2=1$ )。

${\bar{v}}_{AB}$ 的计算方法如下：

${\bar{v}}_{AB}=\frac{L}{\frac{1}{N}{\displaystyle \underset{i}{\overset{N}{\sum }}\left(t_{i出}-t_{i入}\right)}}$ (2)

其中， $t_{i出}-t_{i入}$ 表示第 $i$ 辆车在路段L0上的行驶时间，N表示在统计时间段 $\Delta t$ 内该路段内的车辆总数。

${\bar{v}}_{AB}^{\text{'}}$ 的计算方法如下：

${\bar{v}}_{AB}^{\text{'}}=\frac{1}{k}{\displaystyle \underset{k=1}{\overset{1}{\sum }}\left(\frac{L_k}{\frac{1}{M_k}{\displaystyle \underset{j}{\overset{M_k}{\sum }}\left(t_{j出}-t_{j入}\right)}}\right)}$ (3)

其中， $k$ 表示第 $k$ 支过境交通流， $L_k$ 表示该支交通流对应的路段长度，M_k表示经过分析路段的所有交通流总数。

2.3. 收费站入口控制模型

高速公路发生事故后，可用排队长度来表征事故上游的拥堵情况，确定交通拥堵输入的语言变量值， $\tilde{A}=\left\{\widetilde{A_i}:i=1,2,\cdots ,N\right\}$ ，其中， $\widetilde{A_i}$ 根据人类的语言习惯可取诸如{轻微，中等，严重，非常严重}，用以度量交通拥堵的严重程度，根据工作人员的判断，通过系统中的下拉控件选择相应的等级；各语言值的隶属度函数可取三角形、钟形、梯形，或离散型等多种类型，三角形隶属度函数示例如图2所示。

确定各等级交通事件的区域影响范围R和时间影响长度T的语言变量及其相应的隶属度函数。区域影响范围R是以事件发生地点为原点，以r为半径的圆形或椭圆形区域，其语言变量值可取为 $\tilde{R}=\left\{\widetilde{R_j}:j=1,2,\cdots ,M\right\}$ ，其中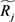根据人类的语言习惯可取诸如{很小、较小、小、中等、较大、很大}等值；区域影响范围和时间影响长度的隶属度亦可取三角形、钟形、梯形，或离散型等多种类型，区域影响范围的梯形隶属度函数示例如图3所示。

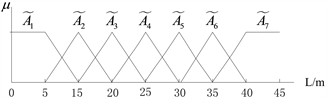
Figure 2. Membership function of event severity

图2. 事件严重程度隶属度函数

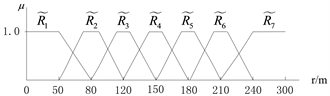
Figure 3. Membership function of regional influence range

图3. 区域影响范围隶属度函数

时间影响长度T的语言变量值 $\tilde{T}=\left\{\widetilde{T_k}:k=1,2,\cdots ,K\right\}$ ，其中 $\widetilde{T_k}$ 根据人类的语言习惯可取为诸如{很短、较短、中等、较长、很长}等值，论域为 $X$ ，划分为7个等级，即 $x=\left\{1,2,3,4,5,6,7\right\}$ ，模糊子集为

$\left\{VS,S,M,L,VL\right\}$ ，其相应隶属度值如表1；表示各模糊子集值在等级X中对应的隶属度值。

Table 1. The corresponding membership values of each fuzzy subset value in rank X

表1. 各模糊子集值在等级X中对应的隶属度值表

以上三角形和梯形隶属度函数构成专家系统知识库中的主要内容。专家系统知识库的规则库，用来存放全部模糊控制规则，在推理时为“推理机”提供控制规则。第i条推理规则为

$R_p$ ：IF $\tilde{A}$ is $\widetilde{A_i}$ THEN $\tilde{R}$ is $\widetilde{R_j}$ AND $\tilde{T}$ is $\widetilde{T_k}$

全局规则库为： $R={\displaystyle \underset{p}{\cup }{R}_p}$

建立推理机。推理机在模糊控制器中的功能是：根据输入的模糊量和知识库(数据库、规则库)完成模糊推理，并求解模糊关系方程，从而获得模糊控制量。已知实时获取的道路交通事件严重程度为A，则输出的模糊集U可由模糊推理的合成算法获得，即

$\underset{˜}{U}=\underset{˜}{A}\cdot \underset{˜}{R}$ (4)

解模糊或清晰化接口方法，可采用最大隶属度判决法、加权平均判决法，和中位数法等，其中加权平均法方法如下：

$u^{*}=\frac{{\displaystyle \underset{i=1}{\overset{n}{\sum }}\mu {\underset{˜}{U}}_1\left(u_i\right)u_i}}{{\displaystyle \underset{i=1}{\overset{n}{\sum }}\mu {\underset{˜}{U}}_1\left(u_i\right)}}$ (5)

至此，可根据实时道路交通拥堵检测结果，推理得到应该实施交通管制的入口个数和管制时间。

3. 交通事故参数设置及仿真

3.1. 仿真参数设置

利用VISSIM软件对高速公路基本路段进行微观仿真，具体步骤如下 [3] [4] [5] [6] 。

设计一条长约70 km的单向3车道高速公路基本路段的仿真模型。由于青临高速公路几何条件对交通流特性影响较小，所以在设计该基本路段的仿真模型时，将行车道宽度统一设为3.75 m，纵坡设计为0，平曲线和限速标志等均按理想条件下设置。

模拟交通事故。交通事故根据其发生的时间、路段交通特性、事故特征对交通运行有不同程度的影响，因此事故持续的时间也会有相应不同。在本次仿真中，将事故的持续时间设定为20 min、30 min、45 min、60 min四种情况。在路段模型上设置三个收费站入口，在距离第三个收费站入口下游2000 m处模拟发生交通事故，模拟交通事故发生在第550 s，分别在1750 s、2350 s、3250 s、4150 s结束。

设置数据采集点、排队计数器和停车场。在1999 m处设置数据采集点和排队计数器。在2000 m处设置停车场，利用停车场功能定义事故车辆，改变车辆停靠时间模拟事故持续时间。

设置车辆类型、及车辆速度。根据收费站数据设置高速公路上包括汽车、客车、货车三大种车辆类型。根据上述高速公路流量与速度模型得到各种车辆类型的速度作为仿真速度值。

设置路口的禁行时间。车辆发生事故后，车流由其他路段通行，在收费站入口外侧有另一条道路，因此在外侧道路上设置一个较短的连接器作为临时通行的局部路径。通过设置决策路径的通行时间，通过调整时间段的值作为不同的管控方案。

3.2. 排队长度原始数据的获取

在仿真参数设定中选取最高的仿真精度(1时间步长/仿真s)，每次仿真时间设为7200 s，最大排队长度设为2000 m。一共生成44种不同方案的排队长度数据，用于记录不同事故持续时间的排队计数器获取的排队长度，输出文件格式“.stz”。

VISSIM的排队长度输出文件里记录了平均排队长度、最大排队长度、停车次数，表2列出了事故持续20分钟不实施管控方案时仿真的部分输出数据。

Table 2. Data table of “queue length” part

表2. “排队长度”部分数据表

Continued

由表中数据可以看出，排队的情况开始出现在600秒时，符合系统设定550秒开始发生事故，平均排队长度的最大值出现在1800秒时，最大值达到了713米。从2040秒开始，排队时间清零，代表事故清理完成，道路恢复正常运行。

4. 仿真方案对比分析

当仿真时的车辆类型、比例以及数量完全相同，改变收费站入口的禁行时间和收费站入口的数量，研究事故持续时间不同的情况下，事故上游的平均排队长度变化规律，分析采取哪一种管控方案时事故的影响时间范围和空间范围最小。仿真结果如图4所示。

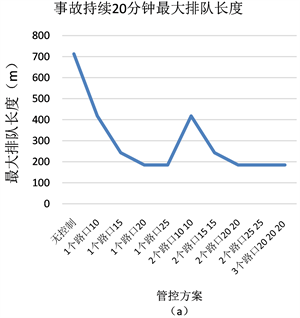
Figure 4. Comparison of control plans under different accident duration

图4. 不同事故持续时间下管控方案对比图

通过仿真不同的事故持续时间，统计原始数据文件，以管控最少收费站入口个数和管控时间最短为最佳方案，最佳管控方案结果如表3所示：

Table 3. Best management and control plan

表3. 最佳管控方案表

5. 结论

通过不同事故持续时间的比较，可得当事故持续时间低于20分钟时，控制上游第一个收费站入口即可，且管控时间为事故持续时间；当事故持续时间为20分钟至30分钟，需要控制上游的两个收费站入口，管控时间为事故持续时间；当事故持续时间在30分钟至60分钟内，需要控制上游三个收费站入口，管控时间为事故持续时间。随着事故持续时间的增加，交通影响时间范围和空间范围随之增加，所以控制入口的个数和时间也会增加。

基金项目

山东省优秀中青年科学家科研奖励基金资助项目(BS2014DX011)；山东省自然科学基金项目“基于车载互联的多尺度路网状态辨识与诱导控制研究”(ZR2012FL02)山东省高等学校科技计划项目“道路交通系统的粗糙集模型与控制方法研究”(J10LG52)。