1. 引言
混沌是非线性动力系统中的一种新的存在形式,是非线性动力系统的一个重要组成部分。混沌貌似有序却又无序,存在一定的确定性现象又不缺乏随机性。混沌系统具有正的Lyapunov指数,对于初始值的选取极其敏感,很微小的变化都会导致出现不同的结果。2008年HP实验室发现的忆阻器实物模型 [1] 引发了忆阻器和基于忆阻器的混沌系统的研究热潮 [2] - [8] 。在通过搭建实际硬件电路来研究混沌系统方面 [9] [10] [11] ,众多的研究者通常只改变某组混沌系统控制参数所对应的电路参数来获取系统吸引子相图,以验证控制参数对于系统的非线性动力特性的影响,并没有分析其系统信号频率范围以及该频率范围的选取范围对于原系统非线性动力特性的影响 [2] - [10] 。文献 [1] 的图2(b)展示了随着频率的增加,忆阻器的伏安特性曲线由100 Hz时所拥有的八字环型在1000 Hz时坍塌为一条直线,此结果揭示在基于忆阻器的混沌电路实现中,由于忆阻器元器件的伏安特性将会随着信号频率的改变而变化,混沌电路信号的震荡频率范围改变可能对系统的非线性动力特性产生潜在影响。本研究以简化Lorenz系统为例,分析积分电路的参数配置对混沌系统信号的震荡频率范围改变及其对于非线性动力系统特性的潜在影响。
2. 简化Lorenz系统
简化Lorenz系统数学模型如(1)式所示,它具有丰富的动力学特性,其系统参数c在[−1.59, 7.75]的范围内取值时系统处于混沌状态,当取值为−1时,该系统为经典的Lorenz系统 [9] [10] [11] [12] [13] 。
(1)
经变量比例压缩及时间尺度变换,数学模型(1)所对应的电路模型状态方程如(2)所示。改变电路模型的可调电阻R14的阻值可以等效为改变系统(1)中参数c的值。
(2)
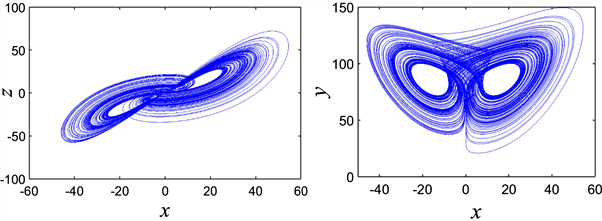
Figure 1. Phase portraits of chaotic attractor (x-y plane, x-z plane)
图1. 混沌吸引子相图(x-y平面,x-z平面)
图1给出了当参数c = 3.4时方程(1)的MATLAB仿真结果,显示系统在该参数下处于混沌状态。
电路模型状态方程(2)的实现涉及时间尺度变换即积分电路中电阻R及电容C的配置。积分电路在滤波电路中属于低通滤波器的一种,对于信号中的高频信息具有抑制作用。由于积分电路的电阻电容的取值决定积分时间常数τ (= RC)及滤波截止频率f0 (=1/(2πRC)),因此在混沌硬件电路的实现时需考虑由积分电路电阻电容参数的不同配置而导致系统信号频率震荡范围的改变是否会影响系统其它器件的电路特性,以及是否会进一步影响混沌系统的非线性动力特性。例如文献 [1] 提出的HP忆阻器以及文献 [14] [15] [16] 中提及的忆阻器模型只在一定频带上保持着忆阻器的相关特性,并非在全频带上保持相同的特性。 [1] [14] [15] [16] 。
图2中,保持R14 = 3.4 kΩ (对应模型1的c = 3.4)及积分电阻R = 1 kΩ参数不变,分别设置积分电容C为1 nF、100 nF及4.7 uF,通过Multisim仿真观察系统的信号频谱,分析积分时间常数对于混沌电路的影响。
图3给出了简化Lorenz电路的系统信号在不同积分常数下的时域图,横坐标分别为每一大格1 ms (图a)、20 ms (图b)和1 s (图c),纵坐标均表示每大格5 V电压。图4显示该简化Lorenz电路系统信号的频谱图(对应图3的时域图),横坐标分别为每格10 kHz (图a)、100 Hz (图b)和20 Hz (图c)。观察图4的频谱图可知,采用1 nF电容时,震荡信号基本落在f < 80 kHz (滤波电路截止频率为f0 = 159.2 KHz)的范围之内,而采用电容C = 100 nF和C = 4.7 uF时,信号震荡频率分别只存在于f < 700 Hz (滤波电路截止频率为f0 = 1592.4 Hz)和f < 20 Hz (滤波电路截止频率为f0 = 33.9 Hz)的范围之内。非线性动力系统信号的震荡频率范围会随着积分时间常数的改变而改变,系统最高的信号频率小于积分电路所设定的信号截止频率。
图5给出了在混沌系统控制参数c对应的电路可调电阻R14的不同取值及不同积分常数的情况下,系统从混沌状态过度到非混沌状态时的双环面现象时吸引子相图,当积分时间常数选用0.0047 s或10−4 s时,增大可调电阻器R14阻值至7.38 kΩ时系统从混沌状态转移至非混沌状态,并呈现出周期为2的环面现象。
由图3至图5可以看出,对于简化Lorenz混沌电路R14的取值决定该电路的系统状态,积分时间常数的选取不同不会改变该系统的非线性动力特性。随着积分时间常数的逐渐增大,时域信号变化速度渐缓,相轨迹在相同时间内表现得越稀疏,导致不容易在示波器上观测到完整的轨迹连续混沌吸引子相图,

Figure 2. Circuit of simplified Lorenz system
图2. 简化Lorenz电路图
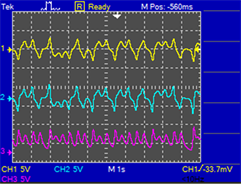
Figure 3. The signals x(t), y(t), z(t) of simplified Lorenz circuit (R = 1 kΩ, R14 = 3.4 kΩ). (a) C = 1 nF; (b) C = 100 nF; (c) C = 4.7 uF
图3. 简化Lorenz电路信号x(t),y(t),z(t)时域图(R = 1 kΩ, R14 = 3.4 kΩ)。(a) C = 1 nF;(b) C = 100 nF;(c) C = 4.7 uF
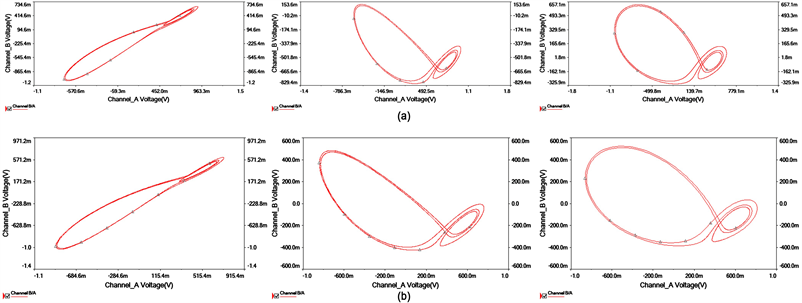

Figure 5. Phase portraits of attractors with different parameters. (a) R14 = 7.38 kΩ, C = 4.7 uF; (b) R14 = 7.38 kΩ, C = 100 nF; (c) R14 = 5.55 kΩ, C = 1 nF
图5. 不同参数下x-y,x-z,y-z平面吸引子相图。(a) R14 = 7.38 kΩ,C = 4.7 uF;(b) R14 = 7.38 kΩ,C = 100 nF;(c) R14 = 5.55 kΩ,C = 1 nF
但系统依旧保持着混沌特性。
图6显示电路在采用不同积分时间常数时(τ = 0.0047 s,τ = 10−4 s,τ = 10−6 s),非混沌状态下的频谱图。可以看出,在相同条件下积分常数取值越大系统信号频率范围越窄,系统频率范围分别为f < 7Hz (图a),f < 300 Hz (图b)。由图6(c)可以看出,此时系统信号比τ = 0.0047 s及τ = 10−4 s时拥有更宽的频率范围(f < 50 kHz)。进一步提高系统输出信号的频率,即缩小积分时间常数使τ = 10−6 s,并逐渐增大可调电阻器R14的阻值。当R14 = 5.55 kΩ时,系统从混沌状态转移到非混沌状态,并呈现出周期为2的环面现象。
由以上分析可知,简化Lorenz电路积分时间常数的取值影响系统的信号频率范围,积分时间常数越大,系统信号震荡频率越低,但并不改变该电路的非线性动力学特性。
3. 结论
在混沌系统的电路实现中,积分电路选取不同的积分时间常数会使得电路的系统信号频率分布范围发生改变。对于简化Lorenz电路,系统在低频范围内由于信号变化速度缓慢,不容易在示波器上观测到轨迹连续的混沌吸引子相图。减小积分电路的时间常数可以提高系统信号频率,在示波器上观测到完整的轨迹连续的混沌吸引子相图,但不会改变系统的混沌特性。这意味着积分电路参数的改变仅仅导致简化Lorenz电路的系统信号频率范围发生改变,不会改变原系统的非线性动力特性。在基于忆阻器的混沌电路中,由于忆阻器的伏安特性会随着系统信号频率范围的变化而改变,考虑到混沌电路本身对于系统初值的高度敏感性,系统信号的震荡频率范围改变可能对原动力系统的非线性动力特性产生潜在影响,此影响需要在后续的研究与实验中加以探索和验证。
基金项目
广东省自然科学基金资助项目(2014A030313510)。
NOTES
*通讯作者。