1. 引言
1963年数学家Lorenz发表了题为“确定性的非周期流”的文章 [1] ,刊登在著名的《大气科学杂志》上。基于对流问题的研究,Lorenz提出了一个可以描述天气变化情况的常微分方程组,得出了初始值的极其微小的变化也可以引起天气十分巨大变化的结论。于是著名的“蝴蝶效应”就诞生了:“一只蝴蝶在巴西轻轻地拍动几下翅膀,有可能在三个月后引起美国得克萨斯州的的一场龙卷风”。由于首次提出了该理论,Lorenz被称为“混沌学之父”。
由于混沌理论在物理学、生物科学、应用数学、保密通讯等领域的应用及潜在的应用价值,使得混沌的控制与同步的研究成为举世瞩目的热点 [2] [3] [4] [5] [6]。1989年Huler首次发表论文提出了混沌控制的概念及方法 [7] ,之后,Ott等人提出了著名的混沌控制的OGY方法 [8]。1990年Pecora和Carroll发现了混沌同步并首次提出了一种混沌自同步的方案 [9]。到目前为止,对于整数阶混沌系统的混沌同步控制的研究已经取得了大量的研究成果 [10] - [15]。
本文简要介绍了混沌的两种定义,对混沌系统的同步进行了概述并介绍了四种混沌同步方法,对存在外部干扰的分数阶超混沌系统的鲁棒同步 [16] 进行了研究,最后给出了全文的结论。
2. 混沌的定义
以下从混沌的不同角度给出了两种影响较为广泛的定义。
2.1. Li-Yorke的混沌定义
1975年发表在美国《数学月刊》的一篇题为“周期3蕴含混沌”的论文,第一次提出了“混沌”一词并给出了其数学表示形式,该混沌定义被称为Li-Yorke定义 [17]。
首先,在一个区间
上,定义一个自身的、连续的、单参数的映射
,
,
. (1)
它的点映射的表示形式为
,
. (2)
定义1对于一个映射
,
,如果它是连续映射或者点映射,而且满足下面的两个条件,那么它是混沌的。
1) 存在一切周期的周期点;
2) 存在不可数子集
,使得
,
,
, (3)
,
,
, (4)
,
,p为周期点。 (5)
其中,
不含周期点。
上述定义中
,
,
说明点相当集,但
,
,
又说明点相当分散;
,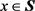 ,则说明子集不会趋近于任意点。
,则说明子集不会趋近于任意点。
同时,Li-Yorke提出了具有混沌动力学行为的Logistic映射
,
,
,当
时,Logistic映射呈现混沌现象。
2.2. Devaney的混沌定义
美国著名数学家Robert L. Devaney从拓扑的角度给出了另外一种混沌的定义。
定义2关于度量空间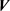 的一个连续映射
是混沌的,如果:
的一个连续映射
是混沌的,如果:
1) f对初始条件具有敏感依赖性。对任意
和
,在x的领域中存在y及自然数n,使得
。
2) f是拓扑传递的。对
上的任意开集X和Y,存在
,使得
。
3) f的周期点集在
中稠密。
在Devaney的混沌定义中,对初始条件具有敏感依赖性意味着只要x和y不完全相等,无论它们相差多小,在f的多次作用后两者之间的距离d都会扩大到一定的程度(
)对于这样的映射f,初始值任意微小的变化都会会使得出的实际结果与理想值产生非常大的差别。第二个条件拓扑传递性则表明任意一点在f的持续作用下将会遍及给定的度量空间
。第三个条件表示系统具有稠密的混沌运动周期轨道。
3. 混沌系统同步概述
1990年,Ott和York在发表的《混沌控制》一文中提出了混沌控制的参数扰动方法,即OGY方法,将混沌系统的运动成功地镇定在不稳定的周期轨道上。1990年Pecora和Carroll提出混沌同步的概念,并将其成功应用于保密通信。混沌同步从本质上来讲是一种广义的混沌控制,是指使两个混沌系统的运动轨道逐渐趋于一致并保持稳定。混沌同步的类型主要有:完全同步、投影同步、相同步、延迟同步等。目前,许多新的混沌同步方法不断地被提出,如脉冲同步法、函数投影同步、鲁棒同步、观测器同步法等。
3.1. 混沌同步方法
3.1.1. 鲁棒同步
假定分数阶超混沌系统的驱动系统为:
, (6)
其中,
为状态变量,
为连续向量函数,
为系统阶数。
假设响应系统为:
, (7)
其中,
为状态变量,
为连续向量函数,
是我们要设计的控制器,
为系统(7)的外部干扰,
为系统参数。
定义同步误差为
,如果通过设计合适的控制器
,可以使同步误差
成立(
为我们设定的一个较小的常数),那么就称驱动系统与响应系统实现了鲁棒同步。
3.1.2. 脉冲同步
在脉冲同步中,驱动系统的形式描述如下:
, (8)
是连续函数,
代表状态变量。
响应系统的形式如下:
(9)
是
阶矩阵,
。定义一个不连续的变量集
,满足如下条件:
,当
时,有
。
是驱动系统传递给响应
系统的非连续变量。响应系统的状态在这些变量处随着同步误差而变化。
由驱动系统(8)和响应系统(9)可以得到系统的同步误差动力系统
. (10)
由于驱动系统的状态在时间上是连续的,
在时间变量
处将会是零。
为了实现响应系统(9)与驱动系统(8)之间的渐进同步,即误差动力系统(10)的渐进稳定,需要找出满足条件的控制增益矩
阵和脉冲间隔
。
3.1.3. 投影同步
选取驱动系统与响应系统分别为
, (11)
, (12)
其中,
,
,
为响应系统的控制输入。
设误差
,其中,
为常数比例矩阵,若
(13)
成立,并且
不全为1或者-1,则称驱动系统和响应系统实现了投影同步,
如果
,即
, (14)
则称驱动系统和响应系统实现了混沌完全同步。
如果
,即
, (15)
则称驱动系统和响应系统实现了混沌反同步。
3.1.4. 广义同步
选取驱动系统与响应系统分别为
, (16)
, (17)
若存在矢量映射
,使
(18)
成立,则驱动系统与响应系统获得了广义同步。
广义同步是指在驱动系统与响应系统之间建立一个函数关系。当
等于
(
是一个常数,
)时,广义同步就成为投影同步。
4. 具有扰动的分数阶超混沌系统的异结构鲁棒同步
目前,很多同步方法忽略了系统的不确定性因素,但是在实际应用中混沌系统经常会受到一些外部干扰,这些外部干扰会使一些理论上成立的同步方法在应用中得不到很好的同步效果。在本章中我们同时考虑了驱动系统和响应系统的外部干扰,基于分数阶稳定性理论提出了鲁棒同步的一种新的方案,设计了合适的控制器,并通过数值仿真实现了同维数的两个分数阶超混沌系统的鲁棒同步,并进一步用该同步方案实现了不同维数的分数阶超混沌系统的鲁棒同步。
4.1. 鲁棒同步方案的设计
假定驱动系统为:
, (19)
其中,
为状态变量,
为连续向量函数,
为系统(19)的外部干扰,
为系统阶数。
假定响应系统为:
, (20)
其中,
为状态变量,
为连续向量函数,
是我们要设计的控制器,
为系统(20)的外部干扰,
为系统参数。
定义同步误差为
,那么,通过驱动系统(19)和响应系统
(20)我们可以得到误差动力系统
, (21)
其中,
为系数矩阵,
,
。
设计控制器
, (22)
其中,
,
,其中
为
的对角线元素组成的对角阵。
将式(22)代入式(21)可得新的误差动力系统为:
. (23)
假设外部干扰的范围为
,那么
, (24)
定义
与
之间的系数
,那么可以得到
, (25)
其中,
。
由式(23)和式(25)可得
, (26)
我们控制的目标是:
, (27)
那么,如果
,根据式(24),(26),(27)可得
, (28)
由式(26)和式(28)可知,当满足条件
(29)
时,就可以得到我们的同步要求。
4.2. 数值仿真
4.2.1. 分数阶超混沌系统的鲁棒同步
选取分数阶超混沌Lorenz系统作为驱动系统,在系统中添加外部干扰
得到系统的表示形式如下:
, (30)
选取Gao等人提出的分数阶超混沌Chen系统作为响应系统,在系统中加外部干扰
得到系统的表示形式如下:
, (31)
可得误差动力学方程为:
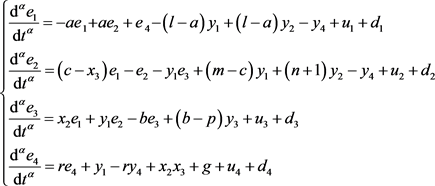 , (32)
, (32)
这里我们构造控制器:
, (33)
将式(33)代入式(32)中,可得误差动力学方程为:
. (34)
假设驱动系统与响应系统的的外部干扰为分别为
,
。那么外部干扰的范围为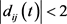 ,
。所以,
。
,
。所以,
。
由式(34)和式(26)可得误差动力系统的系统矩阵
, (35)
由式(29)与式(35)可得
. (36)
驱动系统与响应系统的阶数都取
,取
,那么由式(36)可得
,这里,我们选取
。当选取状态变量初值为状态变量的初值为
,
,此时分数阶超混沌系统(30)和(31)将获得鲁棒同步。同步结果如图1所示。
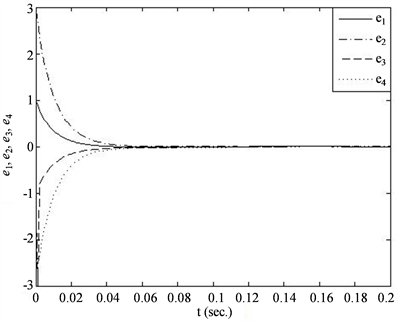
Figure 1. Robust synchronization errors of system (30) and system (31) when
图1.
时系统(30)和(31)的鲁棒同步误差图
取
,那么由式(36)可知当选取
时符合鲁棒同步的条件。当选取状态变量初值为状态变量的初值为
,
,此时分数阶超混沌系统(30)和(31)获得鲁棒同步。同步结果如图2所示。
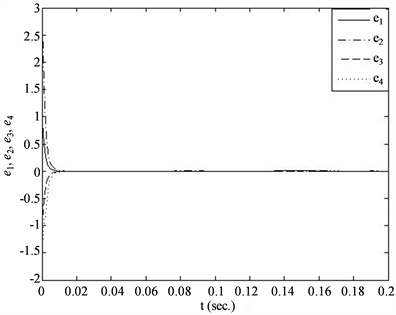
Figure 2. Robust synchronization errors of system (30) and system (31) when
图2.
时系统(30)和(31)的鲁棒同步误差图
5. 结论
本章重点研究了分数阶超混沌系统的一种新的干扰鲁棒同步方法,根据分数阶稳定性理论分析了鲁棒同步的充分条件,通过设计合适的控制器实现了两个存在外部干扰的异结构的分数阶超混沌系统的鲁棒同步,同步误差被控制在原点附近一个半径可控的小的球形区域内,通过改变控制器中参数的设置,可以控制球形区域半径的大小,以获得不同的同步精度。理论分析证明该鲁棒同步方法可广泛适用于分数阶超混沌系统。数值仿真结果进一步证明了该方法可以实现较高精度的鲁棒同步。
由于分数阶超混沌系统更接近于工程实际,而且具有更加复杂的混沌特性,所以成为研究的热点。相对于整数阶混沌系统,关于分数阶超混沌系统的研究还不够成熟,需要广大学者做进一步深入的研究。