基于声光可调谐滤波器角位移补偿方法研究

Study on Compensating the Angular Shift Error of the Acousto-Optic Tunable Filter

摘要: 基于声光可调谐滤波器的偏振成像光谱仪是一类同时具有成像、光谱测量和偏振测量功能的新型光电传感器。非共线声光可调谐滤波器(AOTF)可以快速获得全视场不同窄谱段的o光和e光偏振图像。但是，AOTF波长调谐时，衍射角会随扫描波长的变化而变化，造成同一目标不同谱段的图像发生相对偏移。本文介绍了非共线AOTF的工作原理，分析了基于声光可调谐滤波器的偏振成像光谱仪角位移产生的机理，对近些年来国内外的成像光谱偏振仪的基于声光可调谐滤波器的偏振成像光谱仪角位移补偿方法研究进行了总结分析，对于旋转平面反射镜方法、在晶体出射面加工楔角的方法、棱镜补偿方法、单晶体光楔补偿方法、双光楔补偿方法的原理进行了阐述，并对基于声光可调谐滤波器的偏振成像光谱仪的发展趋势进行了展望。

Abstract: AOTF Imaging spectropolarimeter is a type of novel photo electric sensor which integrated the functions of imaging, spectrometry and polarimetry. Non-collinear acousto-optic tunable filter (AOTF) can quickly get the whole field of different narrow-spectrum light with ordinary and ex-traordinary polarization state images. However, AOTF wavelength tuning, the diffraction angle will change with changes in the wavelength scanning, resulting in the same target in different spectral images relative shift occurred. This article describes the non-collinear acousto-optic tunable filter (AOTF) and the basic principles of the angular shift error of the Acousto-optic Tunable Filter. Angular shift error compensation method of polarization imaging spectrometer for acousto-optic tunable filter in recent years was summarized. The principle for rotating mir-ror method, the crystal surface wedge method, the prism compensation method, single crystal optical wedge compensation method, and double wedge compensation method were described, and the development trend of polarization imaging spectrometer based on acousto-optic tunable filter was discussed.

1. 引言

基于声光可调谐滤波器的偏振光谱成像仪是当今国内外的一个热门研究课题，自从声光可调谐滤波器的各项理论的出现，其各项性能和设计原理逐渐被人们所熟悉，人们也越来越对其各种优越的性能感兴趣。比之于其它形式的成像光谱仪，它有很多优点，首先是它除了具有一般成像光谱仪的二维空间信息与一维光谱信息外，还有偏振信息，可以说它是目前获取信息最多的一种光学遥感器。由于AOTF特殊的分光原理，它具有其它传统分光元件所不能比拟的优点，如：1) 体积小，均为固体结构，无运动部件；2) 衍射效率高；3) 电可调谐，光谱扫描速度快；4) 调谐范围宽。其它的优点还有：数据图像输出灵活、结构简单、光谱波段宽、分辨率高等 [1] [2] [3] 。

特别是应用在航天光谱成像领域时，AOTF成像光谱仪具有光谱扫描速度快的优点，传统的光谱分析技术中采用的分光元件(棱镜或是光栅)的光谱仪的光谱获取方式一般是通过推扫来获取目标的光谱信息，这会产生大量的冗余信息。而AOTF具有灵活的光谱调谐性，不需要光谱扫描就能对视场内进行光谱分析，可以快速选择需要的谱段进行光谱分析，大大减少了遥感数据传输的压力。作为一种分光元件，非共线声光可调滤波器的一系列特点使其非常适合于光谱成像领域的应用。另外，声光可调滤波器的波长扫描过程可以在计算机控制下进行，操作上更加方便 [4] [5] [6] 。

美国、日本和欧洲的一些国家在此项技术的应用方面是比较领先的，特别是美国，喷气推进实验室和陆军研究实验室长期以来一直致力于声光可调滤波超光谱成像仪的研究工作，成功研制出了一系列不同探测波段及不同用途的声光可调滤波超光谱成像仪，并将其应用于军事、遥感、农业和医学等领域 [7] - [12] 。

2. 非共线AOTF的工作原理

AOTF是电调谐光学调制器，利用各向异性材料的布拉格衍射原理。通过在晶体中声光耦合对入射光产生衍射，改变激励声波的电驱动器的频率，可以改变衍射光的波长。AOTF的响应时间由声波渡越过光学孔径的时间来决定，一般是是几个微秒 [13] 。

AOTF的装置通常包括一个双折射晶体以及一个粘在晶体上的压电转换器。压电转换器由压电晶体构成，并通过信号线与射频发生器相连。射频发生器发出的射频信号传输到压电转换器，则会在双折射晶体中激励起声波。光波在通过晶体时发生衍射，分解为零级光和衍射光。衍射光可用电荷耦合器件(CCD)等进行检测。

非共线AOTF由声光介质、电声换能器、吸声装置构成，结构如图1所示。

Figure 1. Schematic diagram of AOTF

图1. AOTF原理图

声光可调滤波器是根据各向异性介质内的反常布拉格衍射原理制成的分光元件。声光可调滤波器的结构主要包括声光晶体和键合在其上的压电换能器。压电换能器将加载到其上的电信号转换成在声光晶体内传播的同频率的超声波，超声波在晶体中传播时与入射光波发生相互作用，当满足布拉格衍射条件时入射光将产生布拉格衍射，衍射光的波长与驱动电信号的频率之间一一对应，因而可以通过改变驱动电信号频率来改变衍射光波长。当射频信号加到换能器上时，激励出声波并射入声光介质。为了防止声波反射，透过介质的声波被吸声装置吸收。

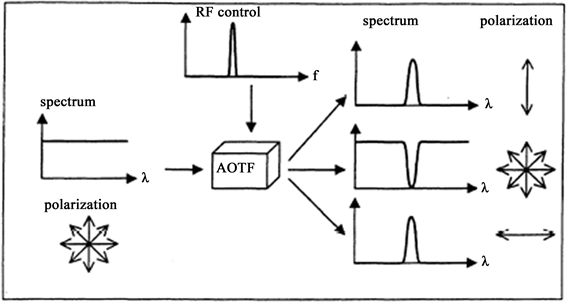
Figure 2. Schematic diagram of white light AOTF incidence

图2. 白光入射AOTF示意图

当入射光为白光时(如图2所示)，对任一声频都将有两束衍射光同时出现，一束为正衍射光，一束为负衍射光，分别位于零级光两侧。正衍射光与负衍射光的偏振态正交。入射光是O光或E光时，只有一束衍射光输出，衍射光偏振态与入射光偏振态正交。当声波频率改变时，满足动量匹配条件的衍射光波长也将相应改变，从而构成电调谐滤光器 [14] 。

3. 声光可调谐滤波器角位移的产生

非共线声光可调谐滤波器(AOTF) ± 1级衍射偏振光的偏转角实际上是波长的函数，随着波长的变化产生变化。在成像的应用中就会出现改变驱动频率，引起衍射波长变化和衍射角变化，造成同一目标不同谱段的图像发生相对偏移，对于TeO₂晶体，o光与e光的主折射率n_o(l)、n_e(l)可由sellmier方程表示出：

$n\left(\lambda \right)=1+\frac{A_1}{{\left(\frac{1}{{\lambda }_1}\right)}^2-{\left(\frac{1}{\lambda }\right)}^2}+\frac{A_2}{{\left(\frac{1}{{\lambda }_2}\right)}^2-{\left(\frac{1}{\lambda }\right)}^2}$

公式中参数A₁、A₂、l₁和l₂的值见表1。

Table 1. Indices of refraction of TeO2

表1. TeO₂晶体折射率计算参数

从公式可以看出，由于TeO₂晶体本身固有的色散性质，o光与e光的折射率n_o、n_e均为波长的函数。

自然光入射到光学系统，晶体受到调制器激发，满足布拉格衍射条件出相对应波长的o光及e光信号，衍射方向由下式确定：

衍射角q_d的计算公式：

$\tan {\theta }_d={\left(\frac{n_o}{n_e}\right)}^2\cdot \tan {\theta }_i$

其中，q_d是衍射光极角，q_i是入射光极角，n_o是o光折射率，n_e是e光折射率。

由衍射光极角与入射光极角的关系式，我们可以得出，对于一定方向的入射光，如果确定了n_e、n_o、衍射角，就可以计算出衍射光的方向。由于n_e、n_o都是光波长l的函数，所以衍射光极角q_d也是光波长的函数。

假设晶体内部的入射光为右旋e光，则由反常声光布拉格衍射原理可知衍射光为左旋o光。从而，入射光折射率n_i以及衍射光折射率n_d分别表示为：

$n_i={\left(\frac{{\cos }^2{\theta }_i}{n_o^2}+\frac{{\sin }^2{\theta }_i}{n_e^2}\right)}^{-\frac{1}{2}}$

$n_d=n_o$

由相位匹配条件，可以得到超声频率与光波长的调谐关系式为

$f_a=\frac{V_a}{{\lambda }_0}{\left(n_i^2+n_d^2-2n_i{n}_d\cos \left({\theta }_i-{\theta }_d\right)\right)}^{\frac{1}{2}}$

其中，f_a为超声频率，V_a为超声声速，l₀为调谐波长。超声频率与衍射光波长的变化关系如图3所示。

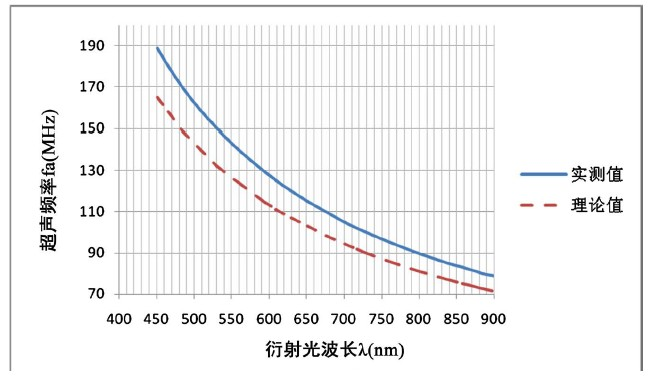
Figure 3. The curve of the relation of the ultrasonic frequency and the wavelength

图3. 超声频率与衍射光波长关系曲线

在成像的应用中就会出现改变驱动频率，引起衍射波长变化和衍射角变化，造成同一目标不同谱段的图像发生相对偏移，因此影响数据的采集应用。

4. 角位移补偿方法

4.1. 旋转平面反射镜方法

1994年，美国NASA戈达德空间飞行中心的D. A. Glenar, J.在他们所研制的地基式望远镜中采用了独立调整两个平面反射镜的方案来补偿色散引起的图像漂移 [15] ，其光学系统结构图如图4所示。

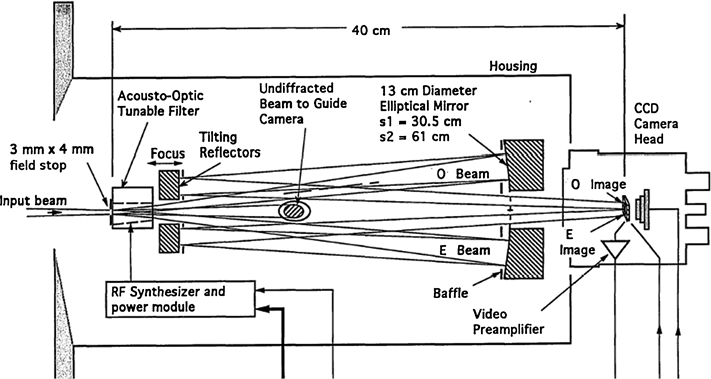
Figure 4. The optical system structure diagram of the polarization imaging spectrometer

图4. 偏振成像光谱仪的光学系统结构图

该种方法补偿最为直接，衍射光的偏移量直接由平面反射镜调整补偿，但是实际应用时需实时精密控制平面反射镜，不同的衍射光波长需调整不同的平面反射镜的角度，这样就失去了声光可调谐滤波器实时性及无运动部件的优越性。

4.2. 在晶体出射面直接加工楔角

1996年，美国宾夕法尼亚州匹兹堡西屋科技中心的D. R. Suhre提出在晶体出射面直接加工楔角的方法来消除晶体衍射引起的色散 [16] 。

消除色散的方法具体可以由图5表示出来，在晶体的出射面上加工上一个大小为q_w的光楔(起作用同色散棱镜)，对衍射光的衍射角进行色散修正。当入射光垂直入射面以极角q_i入射时，晶体中的衍射光的偏转角大小为，( ${\theta }_i-{\theta }_d$ )，衍射光经晶体出射面折射后的折射角大小为b，那么通过折射公式可以得出b大小为：

$\sin \beta =n_o\cdot \sin \left({\theta }_i-{\theta }_d-{\theta }_w\right)$

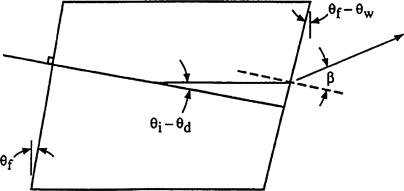
Figure 5. Schematic diagram of the incident plane parallel to the exit surface of AOTF

图5. 入射面平行于出射面时的AOTF示意图

对于确定的入射角q_i，q_d的大小只和晶体的折射率有关，而上面的关系式的右边只有q_d和n_o两个参数与波长的变化相关。如果能选择适当的光锲q_w大小，则可以让两个随波长变化的参数相互抵消而消除出射变化。

这种方法对于消除图像漂移的实际效果可以通过数值模拟加以定量计算。图6给出光楔角取一系列

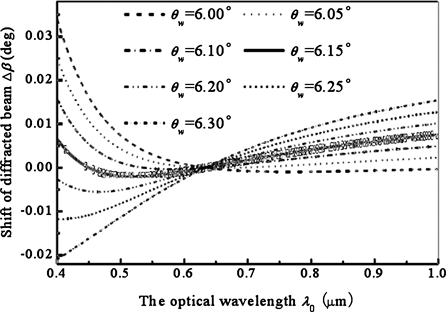
Figure 6. A wedge angle diffraction light varies with wavelength drift

图6. 一定光楔角下介质外衍射光随波长变化的漂移情况

数值时的衍射光漂移情况。从图6可以看出，随着光楔角的增大，介质外衍射光的漂移先逐渐减小，接着达到一个最小值，然后逐渐增大。从图中得到，当光楔角θ_w取6.15˚时，衍射光漂移最小，在波长扫描范围0.4 μm~1.0 μm内，衍射光仅漂移0.00961。

该种方法可以实现色散的补偿，但是实际应用时不能同时经晶体衍射出的两路偏振光进行同时补偿，只适用于偏振光入射到晶体后衍射的补偿应用。

4.3. 棱镜补偿方法

2008年，韩国先进科学技术研究所的Sung Yoon Ryu提出在光路中放置K9棱镜的方法来消除晶体衍射引起的色散 [17] 。

消除色散的方法如棱镜补偿系统图7中所示，由于衍射光波长与棱镜的折射率近似成反比关系，所以棱镜色散角随着折射光的波长而变小。这样，在AOTF后面，沿AOTF光轴传播方向对称放置BK7棱镜，由波长产生的色散现象就可以通过AOTF后面放置的棱镜来补偿，棱镜的底边角度A、B根据补偿的O光和E光设计成不同的值，最终，通过棱镜后的折射角不随波长变化而变化，在CCD接收面上的图像漂移现象也会减到最小。

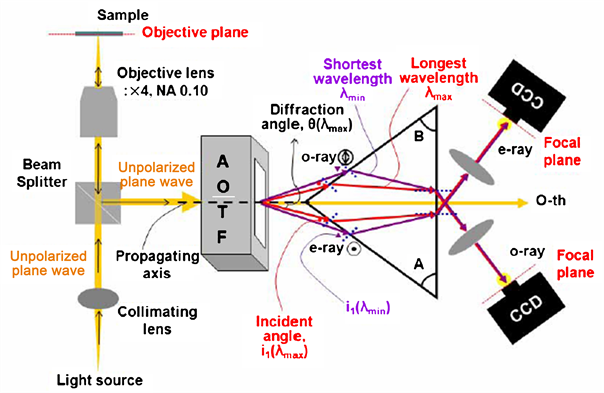
Figure 7. Principle of prism compensation system

图7. 棱镜补偿系统的原理图

在473.95 nm~614.723 nm的波段范围，调谐频率为120 MHZ~180 MHZ，衍射角的变化范围约0.562˚，约为244个像元。在A角 = 46.57˚，B角 = 46.162˚的情况下进行补偿，补偿后图像漂移约为5~6个像元，角度约为0.0012˚~0.0015˚。

该方法可以同时补偿O光和E光两路偏振光的色散现象，但是根据设计结果看，一是补偿的谱段范围不宽，如增大波段范围后补偿的效果非常有限。二是从在AOTF后面放置BK7棱镜的方式来看，该种补偿方式只能适用于光学系统视场角非常小的情况，否则用同一块棱镜来补偿两路偏振光的色散时，两路偏振光存在混叠。三是，相对o光和e光，0级非衍射光能量较强，经过同一块补偿棱镜后会对o光和e光产生较强的干扰，成像时会出现杂光。

4.4. TeO₂单光楔补偿

2009年，本论文作者提出在±1级光路中分别添加晶体单光楔的方法补偿非共线声光可调谐滤波器(AOTF)晶体色散引起的图像漂移。分析结果表明使用TeO₂材料设计的光楔在楔角为7.6˚的时候可以控制图像漂移在一个像元以内，并在400 nm~900 nm的工作波段范围内满足稳定成像的要求 [18] 。

采用TeO₂单光楔补偿的方法从理论上能够很好的补偿非共线声光可调谐滤波器(AOTF)晶体色散引起的图像漂移，但采用晶体材料加工的光楔需要较大的通光口径，这就需要很大的单晶材料，从加工成本及可实现性等方面都存在问题。

4.5. 双光楔补偿方法

2011年，本论文作者提出在±1级光路中分别添加普通光学材料的双光楔方法补偿非共线声光可调谐滤波器(AOTF)晶体色散引起的图像漂移，该方法2013年已获得了国家发明专利授权。

采用普通光学材料的双光楔方法，即使用ZK7与ZF6的组合，在400 nm~900 nm的工作波段范围内可以补偿TeO₂晶体色散引起的图像漂移在一个像元以内，满足了稳定成像的要求。

双光楔补偿的方法如图8所示，通过CODE V光学设计软件程序在晶体中心设置光栅来模拟晶体的偏转及不同波长下的衍射角，由于不同波长下的衍射角具有非线性，存在高阶色散，需要同时优化两个光楔的楔角来达到最优组合。经软件计算对于o光，a₁ = 30.27˚，a₂ = 35.93˚，对于e光a₁ = 30.57˚，a₂ = 36.33˚，材料为ZK7与ZF6的组合。由于衍射偏转角在短波段变化较快，所以评价函数需在短波段加密，并采用自定义的评价函数，使得经过晶体调谐后具有不同衍射角的光线入射到双光楔组后，各个波段的出射方向一致，出射为平行光，即满足了不同谱段的图像经过双光楔补偿后成像在CCD的同一位置。

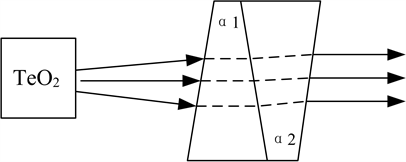
Figure 8. Schematic diagram of double optical wedge

图8. 双光楔补偿示意图

5. 结论

声光可调谐滤波器是一种电调谐光谱滤波器，它最突出的特点是全固体部件并且具有灵活的光谱调谐性。近年来，这种新型的色散元件越来越受到人们的重视，并应用到航天光谱成像领域，它作为的一种新型信息获取方法，综合了成像光谱仪和成像偏振仪的特点，诸多优点和应用前景受到国内外研究人员的广泛关注，目前限制声光可调谐滤波器发展的主要方面为晶体的性能及图像随谱段漂移的问题，文章对近些年来出现的声光可调谐滤波器角位移补偿方法进行了分析总结，并对几种重要类型的补偿方法进行了原理介绍。随着研究的不断发展深入，必将推动基于声光可调谐滤波器的偏振成像光谱仪的创新与发展。

基金项目

国家自然基金(61475190)。

NOTES

^*通讯作者。