1. 引言
随着大机组及大容量远距离输电的快速发展和应用,由机组开停、线路投切、各种短路及断线故障等引起的大规模功率脱落引起的动态频率问题严重影响现代电力系统的安全稳定运行 [1] [2] [3] 。
传统电力系统动态频率安全分析与控制方法均建立在全系统动态频率响应完全同步这一假设的基础上 [4] [5] [6] [7] ,但伴随着大规模互联电网的出现,受扰后的电力系统动态频率响应表现出很强的时空分布特征 [8] [9] [10] [11] 。广域相量测量系统(WMAS)的应用为大规模电力系统动态频率响应时空分布特征的观测提供了有力的工具 [10] [11] 。文献 [10] 利用WAMS记录的不同测点的动态频率录播数据详细分析了受扰后的系统频率的动态过程:频率不仅随时间变化,而且各电气点的频率变化过程亦存在一定的差异。文献 [9] 基于量测信息定义了动态频率响应时空特征矩阵,实现了动态频率响应时空分布特征的量化分析。
目前,对于电力系统动态频率响应时空分布特征的分析仍然集中于对观测数据(WAMS录播数据和全状态时域仿真结果)的分析,此类方法对于事故分析具有重要的意义。但当系统规模较大且量测点较少时,上述方法的有效性和实用性将会受到严重的制约。因此,相对于基于量测的动态频率响应时空分布特征分析方法,利用扰动前的网络结构及运行参数等系统固有特征参数对大规模电力系统动态频率响应的时空分布特性进行分析对指导电力系统运行更具实用价值。
本文通过深入研究多机系统动态频率过程,论证了大规模电力系统动态频率的分区响应特性,并以电力系统结构保持模型 [12] 为基础,结合相对增益矩阵(RGA)理论的最新发展 [13] ,定义了节点间频率耦合系数,节点动态频率关联性的量化分析,进而设计实现了大规模电力系统动态频率响应同频区域辨识方法。仿真分析结果表明:本文定义的节点频率耦合矩阵较好的反映了节点间的动态频率的关联程度,分割所得区域内的动态频率同步度较高。
2. 大规模电力系统动态频率响应特性
2.1. 多机电力系统动态频率过程
当系统由于故障发生较大功率缺额时,系统中个发电机频率将会经历短时间的单调变化过程,继而是振幅不等的振荡过程,整个动态过程主要取决于机组在扰动发生瞬间拾取的不平衡功率 [14] 。
假设在系统节点k处施加冲击负荷扰动
。忽略系统电压影响,发电机采用二阶经典模型,整个网络收缩至发电机内电势节点和负荷扰动节点k,如图1所示。
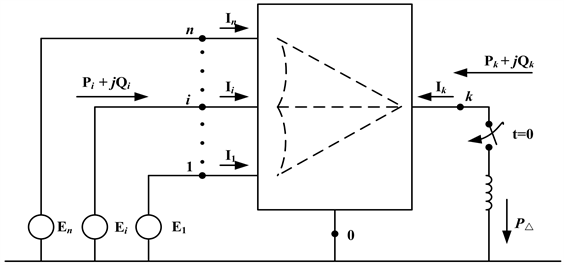
Figure 1. Network after power disturbance at bus k
图1. 节点k发生功率扰动后的网络
假设线路仅考虑电抗,施加扰动后,机组节点注入功率为:
(1)
其中:
,Y为系统导纳阵。
对扰动节点k,有
(2)
对发电机组及节点k处功率进行线性化处理,可得发电机组及节点k功率增量表达式分别为:
(3)
(4)
定义节点i及节点j间的同步功率系数为:
(5)
则有:
(6)
(7)
在节点k处施加功率扰动的直接结果节点k处的相角发生了改变。假设节点电压Vk大小不变,既故障前的
变为
。由于发电机惯性的作用,机组的内电势角不能发生突变。因此,
时刻
,进而,
。由此,发电机组及节点k处的有功功率增量可以表示为:
(8)
(9)
由式(9)可以看出,第i台机组扰动后所拾取的功率
取决于同步功率系数
和
,而
对于所有机组而言是相同的,从而使得发电机组扰动后拾取的功率实际取决于同步功率系数PSik。
显然,对于扰动节点k有
(10)
则有:
(11)
式(11)进一步说明了系统受扰后产生的功率缺额主要根据同步功率系数在系统内相关发电机组间进行分配。从式(5)所示的同步功率系数表达式不难看出电纳Bkj越大,初始角度越小,则机组i所拾取的功率冲击份额越大,既距离扰动点越近,机组承担的有功缺额量越多,而与机组容量及其他参数无关。
将式(11)代入发电机转子运动方程,有:
(12)
其中,Hi为发电机转动惯量,
为机组角频率变化率,
为额定角频率。
因此,结合
和
,在扰动瞬间机组i的频率变化率为:
(13)
式(13)表明,发电机组频率变化率主要由同步功率系数PSik和机组转动惯量Hi决定。而由同步功率系数表达式可知,其大小主要取决于与扰动点的电气距离,进而,发电机组频率变化特点主要由其所在母线在系统中所处的“电气位置”和自身转动惯量的大小决定。
2.2. 动态频率的分区响应特性
对于现代电力系统,并入主干输电网的机组主要以大容量机组为主,机组间的容量及转动惯量较为接近,由上述分可知,当机组间转动惯量相差较小时,各发电机的动态频率变化特征则主要取决于其所在“电气位置”。系统发生有功功率缺额时,系统电压变化幅度相对较小,各母线电压基本维持在额定电压左右,从而,各发电机及母线的“电气位置”主要由系统固有网络结构及参数决定。当两个内部连接相对紧密的子系统通过距离相对较长的输电线路相连接时,受扰后,功率缺额将首先通过联络线在两个区域间进行分配 [14] ,而后根据各发电机在本区域内所处的“电气位置”进行分配。
以图2所示典型三区域互联系统为例,当子系统B内发生功率缺额扰动后,功率缺额将首先通过联络线C1和C3在三个区域间进行分配,各个区域所拾取的有功缺额量将主要由C1及C2的联络线参数决定,在各区域内部,各相关发电机拾取的有功缺额主要取决于其在区域内内所处的“电气位置”。相对于区域间发电机在整个系统内所处“电气位置”,区域内各发电机的“电气位置”距离较近,所拾取的功率缺额相差不大,在转动惯量近似相同的前提下,各区域内部发电机具有较为接近的动态频率响应特性,但由于各区域所拾取的有功缺额大小存在一定的差别,这样就使得各区域表现出不同的动态频率响应特性,既系统动态频率具有分区响应特性。

Figure 2. Schematic of a typical interconnection system
图2. 典型多区域互联系统
基于上述论述,本文将诸如区域A、B及C,内部节点具有相似动态频率响应特征的区域定义为同频区域。
3. 节点间动态频率关联性分析
3.1. 基于结构保持模型的状态空间模型
电力系统结构保持模型由Bergen和Hill于1981年首次提出 [12] ,该模型利用式(14)所示的计及频率阻尼效应的负荷模型将系统全部母线的频率作为状态量保留下来,从而开辟了利用网络信息进行稳定性分析的新思路,并得到了很好地发展 [15] [16] 。
根据结构保持模型原理,对于具有n台发电机,节点总数为m的电力系统,转化为结构保持模型后,节点总数
,其中,节点1~n为虚拟发电机节点,节点
为负荷节点。
假设节点i处负荷为:
(14)
发电机采用二阶经典模型,利用(14)式可得结构保持模型下的节点功率平衡方程为:
(15)
其中:
对于非虚拟发电机节点有:
(16)
在初始运行点处线性化式(16)有:
(17)
其中,
又
,则有:
(18)
式(18)所示状态空间模型反映了系统遭受微小扰动后,节点角频率的变化特性以及不同节点频率变化与其他节点的关系。
假设系统具有均一阻尼,则系统动态特性主要由
决定。对比
元素表达式与式(5)所示的同步功率系数表达式不难发现,当
时,
与节点i与节点j间的同步功率系数具有相同的绝对值,该结论进一步印证了状态矩阵A的非对角线元素在一定程度上反映了节点间动态频率连接关系,因此,可以充分利用状态矩阵A对大规模电力系统动态频率响应特性进行计算和分析。
3.2. 基于RGA的动态频率耦合系数
相对增益矩阵(RGA),由Bristol在1966年提出 [17] ,其初衷是用来以分析多变量控制系统不同控制回路之间的交互影响,以选择合适的输入输出配对方案。此后,经国内外研究人员的不断完善,RGA理论已发展成为一种分析系统变量间交互影响的有效方法,并在多个领域得到了广泛的应用。
定义(Bristol 1966):对于如图3所示的多变量控制系统,定义输入uj与输出yi间的相对增益lij为:
(19)
对于多变量系统,所有的相对增益λij可构成相对增益矩阵
:
(20)
式中
表示矩阵的Hadamard 乘积。

Figure 3. Controlled multivariable system
图3. 多变量控制系统控制回路
根据文献 [18] 分析可知,相对增益矩阵元素λij定量的反映了多变量控制系统输入输出间的耦合关系,其值越大说明输入uj与输出yi间的耦合程度越强。
本文首先基于RGA理论定义节点动态频率耦合矩阵:
(21)
矩阵A为式(18)所示利用结构保持模型线性化全状态阵,若Rij越大,当A阵元aij为定值,
有摄动时,
也将产生大的摄动,表明
与
之间有较强的耦合,既节点i与节点j间动态频率的关联性较强。
由于电力系统自身参数的多样性,且数值变化范围较大,利用(18)式计算得到动态频率耦合矩阵各元素间的亦相差较大,难以直接用于节点频率关联性的量化评估,为了提高动态频率耦合矩阵度量节点频率关联程度的有效性,本文进一步将文献 [13] 提出的DRGA (Decomposed Relative Gain Array)方法应用于动态频率关联性行分析中。
根据文献 [13] 理论,本文定义节点频率相似耦合矩阵
为:
(22)
相对基于RGA理论定义的节点频率耦合矩阵,基于DRGA定义相似耦合矩阵的元素大小均介于[0, 1]区间内,更加突出了输入输出间的耦合关系,能够更有效描述变量间的耦合强度,更加适用于本文的节点间动态频率关联性分析,尤其更适用于动态频率分区响应同频区域的辨识。
3.3. 基于DRGA的动态分区方法
对于大规模电力系统在利用式(18)求得状态矩阵A后,进而利用式(21)和式(22)计算得到系统节点频率相似耦合矩阵
。给定一目标分区数Nc,即可利用下述步骤实现系统的动态分区,进而获得内部动态频率相近的同频区域:
步骤1:初始化临界耦合系数e;
步骤2:在
阵中,舍弃所有耦合系数绝对值小于e的元,即舍弃
阵相应的边,进而A阵的对应边也被舍弃,即认为该边对系统频率的动态行为影响不大。这时系统被分割为一个个的子块,再利用节点联通性搜索各子块相联通的节点;
步骤3:利用步骤2结果计算分区数Nr;
步骤4:比较Nr与期望分区数Nc,如果Nr < Nc,增大e,返回步骤2;
步骤5:结束。
利用本文提出的动态分割方法得到各子区内,节点间动态频率具有较强的关联性,各个子区域内节点动态频率响应具有较强的一致性,可以近似认为各个子区域具有相同的动态频率响应特性。
4. 仿真与分析
本文选用IEEE−118节点系统 [19] 对所提出的理论和算法进行计算和分析。IEEE−118系统由118各节点,118条交流线路,91个负荷节点及19台同步发电机构成,系统结构如图4所示。

Figure 4. IEEE−118 interconnected power system and its partitioning results
图4. IEEE−118系统单线图及分割结果
假设系统具有均一阻尼,在三种不同的运行方式下,首先利用式(21)与式(22)计算其频率耦合矩阵R(A)和相似耦合矩阵
,结果如表所示。
从表1中数据可以看出,运行方式变化对系统节点动态频率关联系数的数值影响较大,不同运行方式下,节点间频率变化的相互影响程度亦会发生一定程度的变化。
同时,利用本文3.3节提出的动态分区方法对IEEE 118节点算例系统在目标分区数分别为2和3两种情况下进行计算。经计算,三种运行方式下,系统3分区和2分区的结果相同,结果如图3所示,但临界关联系数有一定的差别,如表2所示。

Table 1. Results of measure of interaction
表1. 耦合系数计算结果

Table 2. The critical measure of interaction
表2. 临界耦合系数
由不同运行方式下的分区结果可以看出,虽然运行方式对节点间动态频率耦合程度具有一定影响,但对系统频率动态分区结果没有影响。三种运行方式计算所得分区间的联络线均为阻抗值相对较大,线路长度相对较长的输电线路。三种运行方式下分区间联络线输送功率如表所示。
从表3中数据可以看出,三中运行方式下,各分区间的交换功率发生了较大变化,而在分区间的联络连传输功率在发生较大改变的情况下,利用本文提出的动态分区方法所得的分区相同,该结果表明系统动态频率分区响应特性与系统网络结构及参数具有较强的关联性,既在系统网络结构和基本运行方式已知的情况下,其动态频率分区响应特征也可同时确定。

Table 3. The load flow between different area
表3. 不同方式下的区域间交换功率
现有研究表明,大规模电力系统动态频率响应的时空分布特性与系统网络结构参数、扰动位置和扰动量均有关,但却忽略了大规模电力系统动态频率的分区响应特性及其影响因素分析,通过本文建立的节点动态频率耦合矩阵及上述计算表明,大规模电力系统的动态频率分区响应特征由系统的固有特征决定,受运行方式等外界因素的影响相对较小。下面本文将通过全状态时域仿真对大规模电力系统动态频率的分区响应特性进行深入的分析和研究。
假设分别在方式1和方式2下设置如下两种功率缺额扰动:
Case 1:运行方式1下区域A内发生300 MW有功缺额扰动;
Case 2:运行方式3下区域B内发生150 MW有功缺额扰动;
运行方式1下区域A内发生300 MW有功缺额扰动后,系统母线频率的动态过程及局部放大如图5所示,由图中动态频率响应的局部放大图可以看出,受扰后系统动态频率响应具明显的时空分布特性,且呈现出一定的区域响应特征。为了深入分析故障后系统动态频率响应的时空分布特征,本文采用文献 [9] 方法利用相关母线的动态频率响应数据计算得到Cas1扰动下部分具有代表性母线的动态频率响应时空分布特征矩阵,如表4所示。从表4数据可以看出,各母线的最大频率偏移非常接近,无法体现动态频率响应的时空分布特征,但从平均频率变化率、响应延时和最大偏移延时三个特征的计算结果可以很容易看出受扰后系统的动态频率响应的时空分布特征。同时,表3数据表明,利用本文动态分割算法所得A、B、C三个子区域内代表节点具有相似的动态频率响应特征。在此,重点考察各子区域内与其他子区相连的联络节点(A区中的节点37、38、72;B区中的节点43、71、99;C区中的节点100、96。)的动态频率特征,不难看出,各联络节点的动态频率特征与所属区域内其他节点的动态频率特征较为接近,而与所连接的区域的动态频率特征有着明显的差别,整体动态频率响应时空分布特征与本分所得结果一致。

Table 4. Space-time distribution matrix of Case 1
表4. Case 1扰动下的时空分布特征矩阵


Figure 5. Dynamic frequency response of Case 1
图5. Case 1扰动下动态频率响应曲线
受扰后系统频率动态响应时空分布特征分析结果表明,系统动态频率响应的时空分布具有一定区域性,与本文提出的电力系统动态频率分区响应一致,同时,基于动态频率响应曲线的时空特征分析也充分验证了本文提出的动态分割结果的正确性和有效性。
Case 2的动态频率响应如图6所示,其时空分布特征矩阵计算结果如表5。Case 2的计算结果同样表明,受扰后的系统动态频率所表现出的分区响应特性与本文分割结果相同,限于篇幅,本文在此不再做详细分析。
上述分析表明,在不同的运行方式及不同的扰动方式下,系统表现出的动态频率分区响应特性相同。不同运行方式及不同扰动下,系统动态频率响应具有不同的时空分布特征,但其动态频率分区响应不变,主要由系统结构及参数等固有特性决定。根据系统固有特性对系统进行动态分割,进而分析系统动态频率分区响应特性,对电力系统动态频率紧急控制,保证电力系统安全稳定运行具有重要的指导作用。
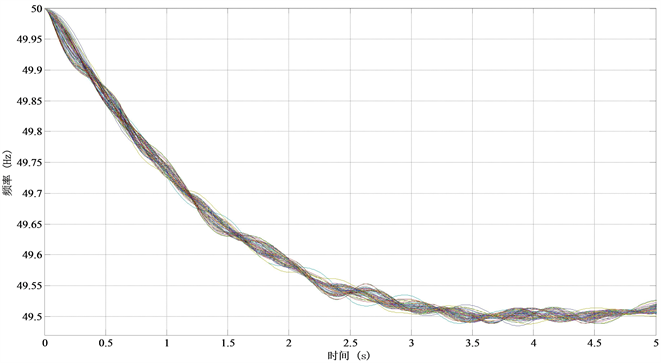

Figure 6. Dynamic frequency response of Case 2
图6. Case 2扰动下动态频率响应曲线

Table 5. Space-time distribution matrix of Case 2
表5. Case 2扰动下的时空分布特征矩阵
Continued
5. 结论
基于对多机电力系统频率动态过程的深入分析,本文定义了电力系统动态频率的分区响应特性,并给出了用于动态频率分区响应分析的动态分割算法,该方法在量化节点间动态频率耦合关系的基础上,实现了电力系统动态频率响应的同频区域辨识。仿真计算结果与分析表明:
1) 电力系统动态频率响应具有明显的分区响应特征;
2) 电力系统动态频率的分区响应由系统结构及参数等固有特性决定,与运行方式及扰动大小和位置无关;
3) 本文提出的动态分区方法物理概念清晰,实现简单,所得分区内各节点的动态频率响应的时空分布特征相近;
4) 动态频率分区响应特性分析结果对电力系统动态频率紧急控制方案设计具有重要的指导作用。
本文只是对电力系统动态频率分区响应特征分析进行的初步试探性研究,如何利用分析结果对电力系统动态频率紧急控制方案进行有设计是作者需要进一步深入开展的研究内容。
基金项目
中国南方电网有限责任公司科技项目(073000KK52180003)。