量子纠缠的相关性判据

The Correlation Criterion of QuantumEntanglement

摘要: 量子态可分性判断是量子纠缠理论的基本问题。本文根据两体纯态的Schmidt分解，给出了矩阵的秩，向量组的相关性判据。对于两体混合态，给出了可分的一个充分非必要条件，并举例说明。

Abstract: The separability judgment of quantum states is the basic problem of quantum entanglement theory. In this paper, based on Schmidt decomposition of two-body pure states, the correlation criteria of matrix rank and vector group are given. For the two-body mixed state, a sufficient and unnecessary condition for separability is given, and an example is given.

1. 引言

量子纠缠在量子力学的基础理论中占据了重要的位置，并且在量子信息的应用中也是不可或缺的资源 [1] [2] [3] 。量子态可分性判断 [4] [5] 是量子纠缠理论的基本问题，量子纯态对应于相应的Hilbert空间的一个单位向量，量子混合态对应于作用于Hilbert空间中迹为1的正算子，其表现形式为密度矩阵，对于复合的量子系统，遇到的问题是量子态是否可分的问题，常用的方法有所谓的PPT (Partial Positive Transposition)判据，矩阵重排判据(realignment criterion)，约化密度矩阵判据(reduced density matrixcriterion)，CCN判据(Computable Cross Norm)等。

2. 量子纯态与复合系统

任意一个孤立的物理系统，与该系统的状态空间H相联系。H为规定了复内积的可分的Hilbert空间，该系统完全由单位化的状态向量来表示。量子比特(qubit)与二维状态空间 $H^2$ 相对应， $H^2$ 取标准正交基 $|0\rangle$ ， $|1\rangle$ ，则任一状态向量 $|\phi \rangle =\alpha |0\rangle +\beta |1\rangle$ ，其中 $\alpha ,\beta \in C$ 且 ${\left|\alpha \right|}^2+{\left|\beta \right|}^2=1$ 。H中的单位向量也称为量子纯态 [1] ，对应于秩为1的密度矩阵 $\rho =|\phi \rangle \langle \phi |$ 。

给定若干个量子系统，通过张量积运算，形成复合系统。 $H_A\otimes H_B$ 表示复合系统AB，若取 $H_A$ 的一组标准正交基记为 $|i\rangle ,i=1,2,\cdots ,m$ ，取 $H_B$ 的一组标准正交基记为 $|j\rangle ,j=1,2,\cdots ,n$ ，则 ${|\phi \rangle }_{AB}\in H_A\otimes H_B$ 表示为：

${|\phi \rangle }_{AB}={\displaystyle \underset{i}{\sum }{\displaystyle \underset{j}{\sum }{m}_{ij}}|i\rangle \langle j|}$

记矩阵 $M={\left(m_{ij}\right)}_{m\times n}$ ，并将其按行按列分块得 $M=\left({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_n\right)={\left({\beta }_1,{\beta }_2,\cdots ,{\beta }_m\right)}^{\text{T}}$ 。其行向量对应于子系统 $H_A$ 的向量，列向量对应于子系统 $H_B$ 的向量。

定理1 [1] Schmidt分解定理：

在Hilbert空间 $H_A\otimes H_B$ 的两体复合系统AB中的任何一个纯态 ${|\phi \rangle }_{AB}$ ，一定可以在子系统 $A,B$ 中找到标准正交基 ${|i\rangle }_A{|j\rangle }_B$ 使得 ${|\phi \rangle }_{AB}={\displaystyle \underset{i}{\sum }{\lambda }_i}{|i\rangle }_A{|j\rangle }_B$ ，其中 ${\lambda }_i\ge 0$ ， ${\displaystyle \underset{i}{\sum }{\lambda }_i^2=1}$ ， ${\lambda }_i$ 为矩阵M的奇异值，成为Schmidt系数， ${\lambda }_i$ 非零的个数称为Schmidt秩。

3. 量子纯态纠缠

对于 ${|\phi \rangle }_{AB}\in H_A\otimes H_B$ 若存在 ${|\phi \rangle }_A\in H_A$ ， ${|\phi \rangle }_B\in H_B$ 使得 ${|\phi \rangle }_{AB}={|\phi \rangle }_A{|\phi \rangle }_B$ ，则称量子纯态 ${|\phi \rangle }_{AB}$ 是可分的，否则上纠缠的。

结合Schmidt分解定理，可以得到如下的结论：

定理2 若 ${|\phi \rangle }_{AB}$ 的Schmidt秩为1，则 ${|\phi \rangle }_{AB}$ 是可分纯态，否则为纠缠纯态。

由初等变换不改变矩阵的秩，在矩阵M的奇异值分解中，酉矩阵可以写成若干个初等矩阵之积，进一步可以得到：

推论1 若矩阵M的秩为1，则 ${|\phi \rangle }_{AB}$ 是可分纯态，否则为纠缠纯态。

推论2 矩阵M中，分块得到的列向量组 $\left({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_n\right)$ 或行向量组 $\left({\beta }_1,{\beta }_2,\cdots ,{\beta }_m\right)$ 中得任意两个向量是线性相关的， ${|\phi \rangle }_{AB}$ 是可分纯态，否则为纠缠纯态。

另一方面，对于密度矩阵 $\rho =|\phi \rangle \langle \phi |$ ，此时秩 $\rho =1$ ，所以：

$\rho =|\phi \rangle \langle \phi |=\left({\xi }_1,{\xi }_2,\cdots ,{\xi }_n\right)$

推论3 若向量组 $\left({\xi }_1,{\xi }_2,\cdots ,{\xi }_n\right)$ 中的两两线性相关时，且非零列向量 ${\xi }_i$ 对应的矩阵M的秩为1，则 $\rho$ 是可分纯态，否则为纠缠纯态。

4. 量子混合态纠缠

假设一个量子系综中有系列的纯态 $|{\phi }_i\rangle$ 且每个纯态对应的概率是 $p_i$ $\left(p_i\ge 0\right)$ ，则它的密度矩阵为 [1]

$\rho ={\displaystyle \underset{i}{\sum }{p}_i|{\phi }_i\rangle \langle {\phi }_i|}$

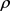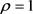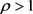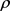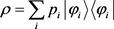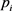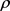其中 $tr\rho ={\displaystyle \underset{i}{\sum }{p}_i=1}$ ，当非零 $p_i$ 的个数大于1时，是混合态，否则为纯态，即秩时为纯态。秩为混合态。另一方面，量子态为作用于H上的迹为1的正算子，其密度矩阵为迹为1的半正定矩阵，进一步可以证明为Hermidt矩阵，其谱分解为，为的特征值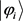，为对应于特征值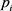的特征向量。

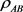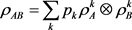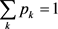对于复合系统AB的密度矩阵，如果能写成，其中，那么称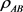是可分的离态，秩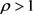为可分离混合态，否则为纠缠态。可以看出对于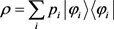，每一个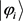都是可分离纯态时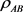，是可分离态，但是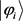，有纠缠态时，则难以判断。例如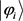为四个bell态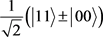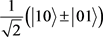，，，此时

；

；

。

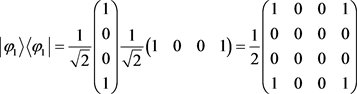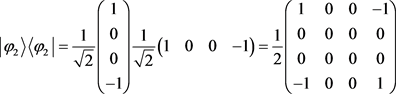
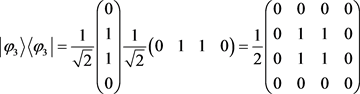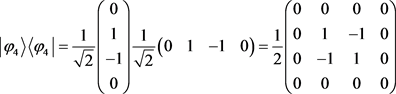进一步计算得到

。

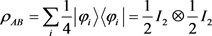量子纠缠是量子物理与经典物理的重要区别之一，1989年，Werner给出了量子纠缠严格的数学定义，本文结合矩阵理论的相关知识，对于两体复合系统的量子纠缠的探测性方法，给出了秩与相关性的判据，并举例说明。