1. 引言
多层材料在传热过程中,不同介质材料会导致不同的温度分布。温度在材料内部随着位置而变化,材料最内侧的温度会随热传递的时间而变化。这类问题从20世纪80年代开始一直被广泛研究。1981年,顾延安研究了保温层外壁面温度,以及它的计算方法,通过理论推导给出了一种计算热损失的方法 [1] 。2007年,白净选用第一类边界条件下的柱坐标形式的导热微分方程对圆筒壁内的温度分布进行计算和分析,得出结论等温面的热流密度相同 [2] 。曾剑等考虑了一类热传导方程中间断扩散系数的反问题,证明了时间相对较小时,极小元的唯一性和稳定性 [3] [4] [5] [6] 。2018年,陈大伟利用热传导方程的差分格式对一维热传导方程的数值解进行计算并绘成图,从而直观地得到热传导媒介上的温度时空分布 [7] 。目前,对于热传导方程解的研究并以此得到热传导媒介在传热过程中的温度分布的相关研究仍在继续,然而对于将两者与隔热材料相结合以提高复合材料的隔热性能以及对隔热时间的研究仍然较少。该研究对于复合材料隔热性能的提高和隔热材料的选择具备参考价值,在实际生活中的应用也较为广泛,可应用于高温作业服、消防隔热墙等诸多领域,因此具有一定的研究价值。
本文通过实验所得实验数据,利用数学物理方程建立稳定状态下的温度分布模型,包括复合介质各分界面的温度变化和多层材料内侧温度随时间的变化。将该热传导模型和实验曲线进行对比,验证模型的正确性。
2. 模型的建立
2.1. 热传递温度分布
将多层介质的传热过程视为沿径向的一维运动,方向由外侧指向内侧,零点为该多层材料最外侧处(如图1)。
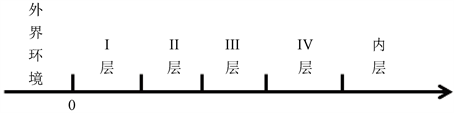
Figure 1. The schematic of one dimensional multi-layered media
图1. 多层介质一维分布示意图
由傅里叶定律和能量守恒定律得出温度随时间和位置变化的方程 [8] :
, (1)
其中
,
为导热系数,c为比热容,
为密度。设多层介质总厚度为d,初值条件满足外界环境温度恒为
,稳定后内侧温度为
,即满足
,
. (2)
分离变量令试探解
,带入(1)求解得 [8] :
, (3)
(
) (4)
其中系数
由初值条件决定,
。方程(1)的一般解可表示为
(5)
设多层介质对应I、II、III、IV层的厚度分别为
,导热系数分别为
。介质中间相邻两层分界面的温度分别为
。对于稳定的导热过程,每一层的导热速率均相等,由热量流守恒条件得每层传递的热量
(
)为
.
这里A为传热横截面积。当热传导处于稳定状态时,有
, (6)
其中
为热阻,
。利用
可求得各层分界面的温度差以及各层面的温度。
2.2. 温度稳定前多层材料最内侧温度随时间的变化
将复合材料两两融合可得出复合材料的密度、热容、导热系数,它们的计算公式为 [9] :
(7)
其中
为相对体积 [9] 。将以上参数带入(5)式可得到复合材料各分界面的温度及内侧温度随时间的变化曲线,结果可表示为
, (8)
其中常系数
、
可通过初始条件和边界条件求出。
3. 计算模拟结果与讨论
以2018年全国大学生数学建模大赛A题实验数据为依托,先进行一个初步验证。实验中各层材料的导热系数、密度及比热容如下表1所示。

Table 1. The parameter for related materials
表1. 各层材料相关参数
外界环境温度恒为75℃,内层初始温度为37℃,传热稳定后内层温度稳定在48.08℃。由(7)可得到复合材料的相关参数:
将以上参数带入(5)并考虑边界条件
,
得:
.
图2给出了该计算结果和实验曲线的对比,从曲线可以看出,上面的关系很好的描述了最内层温度随时间的变化。

Figure 2. Comparison of fitted curve and experimental value
图2. 拟合曲线与实验值对比
同理可以得到I、II层接触面,II、III层接触面,III、IV层接触面的温度随时间变化关系。
I、II层接触面:
.
II、III层接触面:
.
III、IV层接触面:
.
以上温度变化曲线如图3所示(蓝线为I、II层接触面,红线为II、III层接触面,绿线为III、IV层接触面),可以发现,各层传热速率的大小关系为:I > II > III。

Figure 3. The curve for temperature varies as time on three interfaces between layers
图3. 三个接触面的温度随时间变化曲线
4. 实验探究
为了进一步验证稳恒热源热传递的温度分布,去如表2所示的集中材料,分别测量并记录恒温热源的温度和材料层的初始温度。将材料层固定在恒温热源之前并同时开始计时,每隔一分钟测量并记录此刻材料最外层的温度,直至最外层温度稳定,实验结果如图4所示。

Table 2. The parameter for related materials
表2. 各层材料相关参数
实验中,热源恒温为85.7℃,材料的初始温度为26.7℃,材料稳定后的温度为50.0℃。经计算,复合后材料的相关参数为:
理论曲线可求得为:
将实验值与理论曲线对比可知,实验数据与理论曲线基本相符。所以,此模型可运用于符合隔热材料,建筑墙面等的设计中。
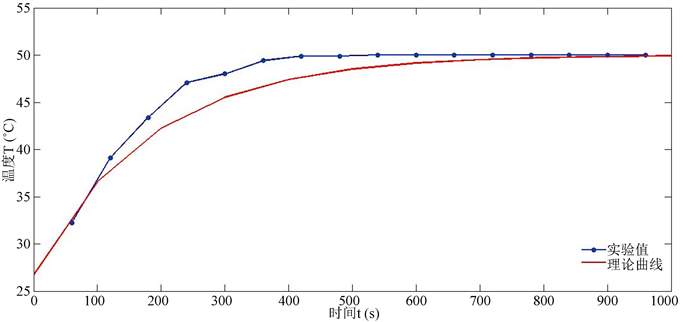
Figure 4. Comparison of fitted curve and experimental value
图4. 拟合曲线与实验值对比
5. 总结
本文将稳定热源沿圆筒径向的热传递抽象为一维过程,用热传导方程研究了多层复合材料的热传导规律。通过复合介质的比热容、热导率和密度参数,我们求出了热稳定后各层介质分界面的温度分布,同时得到了介质内层温度的变化。从理论和实验曲线的对比发现,该模型很好地描述了复合介质的热传导问题。对复合介质的热传导规律的研究在各行各业有着非常广泛的应用,对复合隔热材料的研发有着非常重要的意义。仍需指出,本文只考虑了分离的时间和空间变量;二者同为变量的情况较为复杂,有待进一步深入研究。
NOTES
*通讯作者。