1. 引言
鲁棒控制研究的主要内容是系统存在模型不确定性和外界干扰时,如何设计控制器使得相应的闭环系统具有期望的性能。
鲁棒控制理论对外部扰动具有较强的抑制能力,扇形区域内的极点指标,具有实际工程意义,因此极点配置和
控制是设计控制器的重要方法,在实际应用中有广泛应用。本文求解了同时满足上述两项指标要求的状态输出反馈控制器。
文献 [1] 研究了扇形区域下具有执行器故障的区域极点配置的状态反馈可靠控制问题。文献 [2] 给出了线性系统
可靠跟踪控器存在的充分条件,利用求解LMI完成对
可靠跟踪控制器的设计。文献 [3] 提出了更实际的带有执行器故障扰动的保成本可靠控制问题。文献 [4] 在连续故障的前提下,基于LMI方法给出了反馈控制器存在的充分条件,并且提出了考虑执行器和传感器双故障系统的完整性设计方法。文献 [5] 针对线性定常系统,在不考虑输出的情况下,以执行器故障为前提,给出了扇形区域极点配置的可靠控制率。文献 [6] 针对不确定系统,研究了在混合故障的前提下使极点配置在扇形区域的可靠控制问题。以上文献都是基于单一性能指标的控制问题。文献 [7] 针对具有不确定性的线性定常系统,提出了考虑执行器故障的可靠跟踪控制器设计问题.文献 [8] 是控制理论的基础和概要。文献 [9] 将极点配置和鲁棒控制相结合,研究了含区域极点配置的
控制在舰载机自动着舰控制器设计。文献 [10] 提出一种加权的
优化设计方法来设计挠性系统的鲁棒控制器,以解决采用
回路成形法设计时控制器不稳定且鲁棒性差的问题。文献 [11] 提出了基于
鲁棒控制的光伏并网逆变器控制策略。文献 [12] 利用混合
控制设计某重载车辆悬架控制器,较好的解决了悬架系统性能与系统鲁棒性之间的优化控制问题。文献 [11] [12] [13] 均是单一或多个性能指标控制下的物力学和工程上的建模和应用,可见选题的实用价值。文献 [14] 是针对静态输出,解决区域极点和方差约束的控制问题。文献 [15] 是针对动态输出,解决多指标的满意控制问题。
系统的
控制器可分为次优
控制器和最优
控制器。次优
控制器是指给定的一个上界,寻求一个小于这个上界的范数,且使系统内部稳定的控制器。而最优
控制器是寻求最小的上界,如何使外部扰动对被控输出影响的增益传递函数的无穷范数的上界最小,且使系统内部稳定的控制器。这里考虑次优
控制器问题。
控制能够让系统具有很强的抗有界能量干扰的能力。扇形区域极点配置是指闭环系统的极点配置在左半平面的某个扇形区域内,限制极点的实部和虚部的大小,能够解决系统的不确定等因素的影响下准确的极点配置问题。本文主要研究了在扇形区域下,极点配置的状态反馈
控制的一些问题,数值仿真验证了本文结果的有效性和可行性。
2. 问题描述
考虑线性定常系统:
(1)
其中
为系统的状态变量;
为控制输出;
为控制输出;
为平方可积的外部有界干扰输入;
为适维矩阵。
对线性系统(1)引入状态反馈控制器:
(2)
由此得到闭环系统:
(3)
控制器的设计目的是设计一个控制器
使得闭环系统满足内部稳定,即闭环系统状态矩阵的所有特征值均在左半开复平面中;对于给定的
,从扰动输入
的闭环系统传递函数
的范数小于
,且使得系统内部稳定,从而约束了外部的有界干扰。
系统的
控制器可分为次优
控制器和最优
控制器。次优
控制器为:给定的
,寻求一个
,且使系统内部稳定的控制器。最优
控制器为:寻求最小的
,使
,且使系统内部稳定的控制器。这里考虑次优
控制器问题。
考虑如下系统:
(4)
其中
为系统状态;
为系统的测量输出,
为系统被调输出;
为外部有界干扰输入;
为适维矩阵。
引理1 [7] :(有界实引理)设常数
,则系统(4)是渐近稳定的且
的充分必要条件是存在一个正定对称矩阵
满足:
引理2 [8] :对于闭环系统系统(3),存在状态反馈
控制器,当且仅当存在正定对称矩阵
和矩阵
使得下列线性矩阵不等式(LMIS):
(5)
成立,如果可行解为
,则相应的状态输出反馈控制器为
。
引理3:对于闭环系统(3),存在状态反馈控制器(2)使得闭环系统(4)极点配置在夹角为
的扇形区域内的充分必要条件为对于正定对称矩阵
和矩阵
使得下列线性矩阵不等式(LMI):
(6)
存在可行解。如果可行解为
,则相应的状态输出反馈控制器为
。
其中:
。
3. 主要结论
定理1:对于系统(3),存在一个状态反馈控制器(2),当且仅当存在一个正定矩阵
和
,使得以下的线性矩阵不等式组(LMIS):
(7)
成立,如果(7)存在一个可行性解
,则对于给定的
,系统的状态反馈控制率为
。此时,闭环系统的极点在限制区域内,且
。
证明:
由于式(7)对于变量不是凸的,所以可以令
,这样含区域极点配置的
控制可以转化为凸优化问题。
根据有界实引理,闭环系统(3)是渐近稳定的,且满足性能条件
,当且仅当存在一个正定矩阵
,使得:
成立。对上述不等式的左右两端分别左乘右乘矩阵
,可得等价的矩阵不等式:
设
,即可得到不等式:
同时,由引理2可知把闭环系统(3)的极点配置在规定的扇形区域内必须满足:
整理可得:
设
,故有:
即
状态输出反馈控制器为
。其中
。
综上有:
定理得证。
4. 数值仿真
本文正常的线性定常系统在无故障的情况下,通过设计状态反馈控制器使闭环系统的极点在扇形区域内且满足
性能指标,同时系统达到稳定。
考虑如下系统:
图1表示的是正常的线性系统的开环极点部分不在扇形区域内,可见此系统是不稳定的。其结果是通过MATLAB-LMI工具箱求解了引理2中的线性矩阵不等式得到的,能够保证计算结果的准确性。

Figure 1. Partial poles of open-loop system are not in sector region
图1. 开环系统部分极点不在扇形区域内
图2表示通过设计
控制器,令式(6)中
,其中
,此时系统
范数为1.0356。
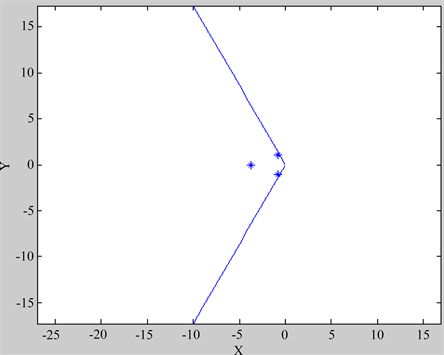
Figure 2. All poles of closed-loop system are in the sector region
图2. 闭环系统所有极点均在扇形区域内
通过求解符合定理1的矩阵不等式的数值仿真,极点配置在了给定的扇形内,且求得的传递函数的
范数小于给定的
值达到了性能指标的要求,说明此系统的极点均配置在扇形内且满足
性能指标,验证了本文定理的可行性。
5. 结论
本文研究了扇形区域下无故障的区域极点配置的状态反馈
控制问题。通过设计控制器使所有极点稳定且可以配置在扇形区域下,并满足具鲁棒
性能水平
。文章中的数值仿真以及极点配置图像证明了可靠控制器的有效性。
参考文献