用众数法和线性插值法及主成分分析法与字符串匹配法——对互联网时代的相亲的研究

Use of the Crowd-Count Method and Linear Interpolation Method and Principal Component Analysis Method and String Matching Method—Research on Blind Dates in the Internet Age

摘要: 互联网的出现给相亲找对象提供了新的快捷途径，本文针对婚介公司提供的数据使用众数法和线性插值法对数据进行修改和填充，对所有婚介公司的会员建立了整体满意度最大的数学模型，对所有婚介公司的会员进行质量的排序，运用主成分分析法对男女会员的数据分别进行处理，最后列出优质男会员优质女会员，对国内婚介公司有着一定的参考价值。

Abstract: The emergence of the Internet provides a new and quick way to find a blind date. In this paper, the data provided by matchmaking companies are modified and filled with the method of number and linear interpolation, and the mathematic model of the overall satisfaction of all matchmaking companies is established. The quality of the members of all matchmaking companies is sorted, and the data of male and female members are processed separately by using the principal component analysis method. Finally, the high-quality male members and high-quality female members are listed, which has a certain reference value for domestic matchmaking companies.

1. 概述

互联网时代的相亲的研究的问题提出：随着社会发展，大龄剩男剩女越来越多，已经成为关注度很高的社会问题，但传统的相亲方式具有人为因素的局限性。互联网的出现给相亲找对象提供了新的快捷途径。但使用软件程序对相亲者进行配对时，需要相亲者提供完整准确的数据，才能使配对结果更加具有合理性。本题针对某婚介公司提供的会员信息，建立合适的数学模型，提高配对的效率，优化配对结果，增加该婚介公司注册会员所推荐对象满意度 [1]。

针对问题一：需要对该婚介公司提供的数据进行修改补充。首先对注册会员的信息加以分类处理，针对数值型数据和分类数据的数据特点，使用众数法和线性插值法对数据进行修改和填充，具体实现需用到spss进行处理。考虑“身高上限”、“身高下限”两指标男女会员填写数据时的特殊性，使用最小残差法对会员身高和其所要求的身高上下限进行拟合，再使用拟合方程对空缺项进行预测填充。

针对问题二：给出使所有会员整体满意度最大的数学模型。本文使用字符串匹配法，将会员要求的指标信息与异性会员的相应指标信息进行匹配，若指标匹配相似度较高，则可得到较高的满意度分值，若匹配不到则退而求其次，相应满意度分值做合理削减。

针对问题三：对所有会员进行质量的排序，最后列出优质男会员优质女会员各20名。基于当代对女性男性略有不同的评价标准，运用主成分分析法对男女会员的数据分别进行处理，处理之前对分类数据进行数值量化，对一些负指标数值数据进行分段等级量化，再将标准化处理之后的数据予以不同的权重，求得所有男女会员的得分，分别排序后得到前20名优质男女会员。

2. 研究的问题细化

2.1. 引言

所谓相亲，无非是通过红娘将素不相识的两个男女约到一起，这未尝不是接触异性的一种好方法。相亲比网恋来得真实，毕竟红娘对对方的家境以及人品有所了解；相亲又比邂逅来得稳妥，一见钟情的感情往往不会长久。所谓配对，是指根据一群男女自身的基本条件及择偶条件，为达到整体满意度最大进行撮合。

21世纪人类进入了互联网时代，人们的物质条件相比过去都有了长足的发展，但是进入现代社会的剩男剩女却越来越多。现在电视上各种相亲节目层出不穷，非常火爆，各种商业性的婚介机构也相继出现。目前市场上的婚介机构运作模式大都是单身男女交纳一定数量的费用成为会员，然后由机构的专业人员将注册会员的信息进行逐项比对，将匹配度较高的单身男女进行配对后，通知双方相亲。但由于注册会员的人数往往数量庞大，仅靠人工进行配对，不仅会存在很多的人为局限性，错过许多良缘，而且工作效率低下。现需要研究某婚恋网站的信息配对系统，如何使该婚恋软件的到更好得被使用 [2]。

2.2. 问题的提出

某婚介机构网站要求加入的会员在上网注册时，填写自身的基本条件和择偶条件，如果哪个会员相亲成功，网站就会抹去相应的信息。眼下网站共有1053位会员，其中男会员有496位，女会员有557位。详细的数据资料见A题附件。

为提高运作效率，网站希望能够通过建立数学模型，解决下面问题。

问题1：由于种种原因，数据资料中存在一些缺失、错误或不按常规要求填写的数据。请进行合理的补充或修正；要求写明补充或修正的依据。

问题2：建立一个可以进行实时配对的数学模型，使得通过该模型运算结果进行配对时，能够使当前会员对配对对象的满意度整体上达到最大。请列出对当前会员运算结果中显示的部分配对情况(比如20对左右)。

问题3：分别按照男会员与女会员的自身基本条件进行排序，要求分别列出前20名优质的男女会员的序号。

3. 问题分析

3.1. 问题一的分析

针对问题一的要求，首先应该筛选出异常值进行剔除，将一些明显不符合常理的数据，先从表中去除掉，为接下来的数据清洗做准备。然后根据会员所给的属性不同指标进行分门别类的补充。同时对于一些汉字的中文信息，通过量化编码把它转变成可分析的数据，接下来我们针对特征不同的数据，分别采用最小绝对残差法和众数法和线性插值法，对数据的空缺进行有效的补充。

3.2. 问题二的分析

针对问题二，是要求我们将会员信息和其要求的对象的信息进行整理，将他们尽可能的进行匹配。不同于问题一，我们将地区因素也算入指标，这样可以更好的反映出最佳的配对情况。然后，将这些信息依次记为编号，记为一个字符串，这样会员的信息和要求对象的信息就变成了一组可比较的字符串。将其逐一进行对比，对比后不通过的则进入下一轮。以此来进行实时配对。最后，通过字符串的相似度比较，得出相似度得分，在经过处理之后，可以得到满意度的值。

3.3. 问题三的分析

针对问题三，问题三是要求对已知会员的信息进行整合，通过一定的标准，把这组数据当中优质的男会员和女会员筛选出来。介于男女会员在选择对象时的标准并不能完全的统一，如年龄一指标对男女会员质量的影响就存在很大的差异，因此我们对男和女分别进行数据的整合和处理由，分别建立数学模型，可使提高处理结果的合理性。通过主成分分析法，对已有数据进行数据标准化，然后进行一个相对合理的打分。分别将男和女两组数据的打分进行排列，最后遴选出20对优质男女会员。同时为了验证这一打分系统的可靠性，我们要通过某一种方式检验这一系统的可靠性。同时，问题三是对会员自身条件进行评判，因此我们在问题三中不把地区作为一个主要因素进行评判。

4. 模型假设

1) 男女会员的所有数据均真实无误。

2) 男女会员的缺失数据为随机缺失。

3) 男女会员在填写配偶要求时，会根据自身的条件去考虑，如女性会员会挑选比自己高的会员。

4) 假设单位类型一项并无前后质量的区别。

5) 假设会员所拥有的房子价值相同。

6) 假设大部分男女会员的婚恋观符合常人的婚恋观念，拥有正确主流的价值观念。

5. 符号说明

符号说明见表1。

Table 1. Symbolic description

表1. 符号说明

6. 模型的建立与求解

6.1. 问题一模型的建立与求解

对于问题一，要对已经给出的数据进行筛选把它们当中的异常值剔除，并且要把空缺值补上，使之具有合理性，从而对后面的问题进行比较良好的处理。对于剔除，我们采取筛选的方法采取合理值进行处理。对于填补空缺值，我们采取插值和拟合等方法进行处理。

6.1.1. 数据的修正

1) 在会员身高一栏处，有1.77 cm的数据，这是误填，将其改为177 cm；有部分数据为0，将其改为空缺值。

2) 在会员和其要求对象的文化程度的数据中有“请选择”，不符合常理，将其改为空缺值。还有数据显示为“不限”，我们通过筛选发现这些数据很少，并不会影响整体大样本的分析，故我们决定也将其删去作为空缺值。

3) 在会员收入中出现了诸多“2~3000”，“2000实习”等字样，这些对处理数据都无法实现，我们将其取为平均值，实现数据的相对离散。在会员要求对象的数，这些均不符合常理，同意改为空缺值。

4) 在年龄差上限和下限中，存在正数负数相间分布的现象，并且对于超过20的数据经分析应该是会员要求对方的实际年龄，为避免混乱，我们将年龄差定义为“会员要求对象的实际年龄–会员自己的实际年龄”，将数据进行清洗。

6.1.2. 数据的填补

首先对于“性别”，“婚姻状况”，“文化程度”等文字信息，必须将其量化成某一具体数值，否则无法对数据进行分析。量化表如下：会员自身情况量化表见表2。会员对配偶各项要求量化表见表3。

Table 2. Quantification of membership status

表2. 会员自身情况量化表

Table 3. Quantitative table of member requirements for spouses

表3. 会员对配偶各项要求量化表

这里面的数据均存在缺失现象，为此我们必须分类讨论，对于不同性质的数据属性，我们要采用不同的方法。

1) 对于“婚姻状况”，“文化程度”，“住房情况”，“地区”，“单位类型”数据，这些数据的共同特征在于，对它们进行量化编码之后，其数字都在0到9之间。经分析之后，会发现其中某一个数字出现的频率在60%到70%之间，为此我们采用众数的填补方法。因为出现频率最高的数字，比例已经过半，所以对于部分空白的填补并不会影响整个数据的分析。通过众数填补方法，可以比较客观的反映这些指标的分布状况。

2) 对于“会员收入”和“会员要求对象的收入”的数据，这两组数据的特征在于它们与其他数据之间的关系，并不存在明显的函数关系。他们的数字，范围比较广，因此不能采用众数的填补方法。因此可以采取线性插值的方法来填补这些数据的空缺值，插值的方法，是将所有数据的点尽可能控制在一条曲线之内，这样可以避免奇异值出现。因此该数据能比较真实的反映输入的真实情况。而后我们将填补后的数据，进行整合分析，如图1、图2所示，通过图形，我们可以发现，无论是“会员收入”还是“会员要求对象的收入”这两栏，没有出现很大的出入，“会员要求对象的收入”总是与“会员收入”基本相一致。在不同的区间都存在一定数量的样本，存在部分过高或过低的值，但是仍然有一定的比例。因此，这种方法实现填补空缺是合理的。会员自身收入分布图见图1；要求配偶收入分布图见图2 [3]。

Figure 1. Distribution of members’ own income

图1. 会员自身收入分布图

Figure 2. Distribution of spousal income required

图2. 要求配偶收入分布图

3) 考虑到一般情况下，会员自身身高与对配偶身高的期望值，即身高上下限，有一定的影响，例如自身身高偏高，就很可能选择身高较高的配偶，或者有些男性会员会要求配偶身高不能高于自己。对于男性女性的择偶标准中的身高上下限的数据缺失部分，可以用数据完整的会员自身身高与其要求的身高上下限所拟合得到的回归曲线进行预测。对已知数据的拟合可用最小绝对残差法对所选自变量——身高，与因变量——配偶身高上限或者下限，进行拟合得到拟合直线，该方法可剔除个别与全局偏差较多的数据，使残差最小，相比于简单的额最小二乘法更适用于该题目，用得到的拟合线性方程在excel中对身高上下限缺失的会员进行身高上下限的预测与计算，得到与之对应的身高上下限。男择女身高上限见图3；男择女身高下限见图4。

Figure 3. Male height ceiling chart

图3. 男择女身高上限

Figure 4. Male height ceiling

图4. 男择女身高下限

运用matlab的cftool拟合工具箱对身高上下限已知的会员身高以及身高上限或下限两列数据进行处理，易得到男会员对配偶的身高上限要求、男会员对配偶的身高下限要求、女会员对配偶的身高上限要求、女会员对配偶的身高下限要求分别如图3、图4、图5、图6。男会员对配偶的身高上限要求、男会员对配偶的身高下限要求、女会员对配偶的身高上限要求、女会员对配偶的身高下限要求的拟合线性直线方程如下：

$\{\begin{array}{l}{y}_1=0.5x+80\\ y_2=0.40x+90.19\\ y_3=0.028x+175.4\\ y_4=0.4x+106\end{array}$ (1)

Figure 5. Female height ceiling

图5. 女择男身高上限

Figure 6. Lower height of female elect male

图6. 女择男身高下限

在运用所得方程预测推算出男女会员对配偶身高上下限的要求之后，做所有会员身高上限下限——包括原始值和预测值的散点图见图7，没有出现不合理的浮动，在一定程度上也说明了该方法合理性。

Figure 7. Scatter of height, upper and lower limits for men and women

图7. 男、女身高上下限散点图

对于年龄差上下限的问题，之前已经给出了相应的公式。会员要求的年龄差上下限这两个数据具有独立性，考虑真实情况，不同人群，对自己要求对象的年龄差的上下限，应该存在一定规律的分布，且有正有负。通过尝试，我们采用序列平均法进行填补数据。这样得出的结果，我们可以明显的看到年龄差上下限，呈一定规律的分布，且有正有负，后端数据近似趋近于正弦型分布，符合现实人们对于对象年龄的要求。年龄差分布折线图见图8。

Figure 8. Distribution of age difference

图8. 年龄差分布折线图

6.2. 问题二的模型建立与求解

针对本问，需要同时考虑会员自身的信息和会员要求对象的信息，且二者要进行匹配，使得最终双方的满意度都达到最高。由于会员要求对象的信息中有地区的信息，因此我们也要把地区因素考虑进去。在变量为地区的数据中，存在部分数据描述方式不统一的情况，例如：数据同时存在“鼓楼区”和“鼓楼”类似这样的地区描述，将所有类似“鼓楼区”的地区描述字符串统一去除行政区划单位，只保留地区名称。例如，将“鼓楼区”处理为“鼓楼”。考虑到需要对会员信息与所要求对象信息进行逐项匹配，我们采用字符串匹配的方法来进行对象的匹配。字符串匹配的方法步骤见图9所示 [4]。

Figure 9. Step diagram of string matching method

图9. 字符串匹配方法步骤图

6.2.1. 模型原理

字符串相似度的是将每个人信息看作是一个字符串，将两个不同用户之间数据进行对比就是将两组相应的字符串进行对比，得到字符串的相似度。此思路主要是因为在7个信息里，其中“3”婚姻、“4”文化程度、“5”单位类型、“6”住房情况，都是表示类型的离散变量，其中仅文化程度的数值大小可以代表文化程度的高低，其余3个变量的取值均没有数字意义，仅代表类别。

字符串相似度计算公式为：

$ratio=2\times M/T$ (2)

其中M为匹配到的字符串对数，T为总的字符串数量，例如：某用户年龄35，婚姻状况“3”，住房情况“2”，单位类型“1”，文化程度“3”。该字符串为“353213”，而用户B年龄37，婚姻状况“2”，住房情况“1”，单位类型“1”，文化程度“3”，该字符串为“372113”。两个字符串共有3对可以匹配到，总计有12个(A，B相加)。则相似度为2 × 3/12 = 0.5。

6.2.2. 模型建立

1) 首先，数据中有些会员是无法找到其匹配程度的，这些会员没有相似度得分，经验证，366个会员无法进行匹配。

2) 接着我们要把可以匹配会员的候选人数找出来，以下表举例。部分会员符合标准异性数量表见表4。同时我们令集合为显示行矩阵，既将会员所匹配对象所在那一行显示出来。由于计算时所用行数与实际行数有一定差别，因此可能不同。部分会员符合标准异性数量表见表4。

Table 4. Some members meet the standard heterosexual scale

表4. 部分会员符合标准异性数量表

3) 进行反向判断

假设会员甲匹配到的对象会员是乙，但是我们需要检验会员乙的要求是否方向符合甲的要求，如果

不符合，那么该会员匹配的相似度不大。因此，我们建立一个反向判断集合 $J=\left\{j_1,j_2,j_3,\cdots ，j_n\right\}$ 来衡量

上述匹配的对象是否反向符合他的要求，该集合里面显示两个值“TRUE”或者“FALSE”来显示该会员是否反向匹配也成功。这一要求会减少匹配的对数，以此，我们找出15组可以通过这一反向验证的最终匹配对象如图示。鉴于空间这里我们只显示会员信息，相似度最高得分和所找最优配对信息。其他的集合内容在附录8.2里。部分会员匹配相似度结果见表5。

Table 5. Partial member matching similarity results

表5. 部分会员匹配相似度结果

6.2.3. 模型分析

通过问题可以知道，需要让所有匹配成功的会员满意度达到最大，因此我们建立一个将每位会员的满意度得分列入一个集合中来分析他们的问题。考虑到会员所匹配对象相似度越大，其满意程度也会越高。我们在这里就将第i个会员所匹配的对象相似度得分矩阵记为：

$S_i=\left\{{\alpha }_1,{\alpha }_2,{\alpha }_3,\cdots ,{\alpha }_n\right\}$ (3)

记 ${\gamma }_i$ 为第i个会员的相似度得分最大值

$r_i=\max \left\{{\alpha }_1,{\alpha }_2,{\alpha }_3,\cdots ,{\alpha }_n\right\}$ (4)

那么最终的满意度记为 $\beta$ ：

$\beta =r_1+r_2+\cdots +r_i$ (5)

在这里我们认为每个人的相似度得分区间为[0, 1]之间。

为了更好的说明所配对会员的满意度最大，我们把所有会员与各自满意度最大的配偶的评分做三维图如图10，x，y轴分别为两组配对对象，纵轴z为两人匹配所得分数，某一性别会员全部拥有满意度切相对较高，说明了模型的合理性。会员配对结果分数分布见图10。

6.3. 问题三的模型建立与假设

6.3.1. 模型分析

本问要求筛选出在几个指标中最优的男女会员各20名。如果把男女统一用一个模型描述处理，会导致结果不精准，因为对于男女会员的最优评价，标准是不一样的，因此在本问中，要对男女会员进行分开处理，建立不同的指标和成分进行分析，从而更加合理地找到优质会员。出成分分析法步骤见图11。

Figure 10. Distribution of member matching results

图10. 会员配对结果分数分布

Figure 11. The steps of component analysis

图11. 出成分分析法步骤

通过对问题的分析，我们知道附件一给出了评判男女会员的多个因素，且这些变量之间具有一定的相关性，鉴于此，可采用主成分分析(PCA)并结合SPSS软件的因子分析对这些因素进行降维处理。

PCA的原理是通过分析得到两个或更多的变量f₁，f₂能够尽可能反映原来多个变量的信息，也就是说它的方差尽量大，而且f₂中的信息并不和f₁中所代表的影响因素所重合，即Cov(f₁, f₂) = 0，Cov表示协方差。主成分分析法已经是一种比较成熟的方法，在此，我们给出简要的分析步骤如图11。

6.3.2. 模型建立过程

1) 权重的确定

本问与前两问不同的地方在于，关于年龄的处理，如果单纯的对年龄进行分析，会导致结果不精准。因此必须将年龄进行量化，同时对于男女的年龄处理，结合实际情况，应该有所不同。如下表6给出了年龄段的分类标准。男性女性年龄分段量化表见表6。

Table 6. Quantified by age segment for males and females

表6. 男性女性年龄分段量化表

2) 数据标准化处理

由于表中给出的数据评判单位不具备统一性，所以必须将这些数据进行标准化，代入分析过程，才能够得到正确的方程。本问中采用Z-Score法进行标准化。

Z-Score通过 $\left(x-\mu \right)/\sigma$ 将两组或多组数据转化为无单位的Z-Score分值，使得数据标准统一化，提高了数据可比性，削弱了数据解释性。这样处理后对于一些信息比如“住房情况”、“婚姻状况”、“文化程度”情况比较方便对比，从而得出相关系数矩阵。

3) 模型求解

Step 1得出相关系数矩阵

我们将会员的“年龄”，“身高”，“婚姻状况”，“文化程度”，“单位类型”，“住房情况”，“收入”分别记为 $x_1,x_2,x_3,x_4,x_5,x_6,x_7$ 。得出主成分矩阵之后，进一步分析得出各个主成分与最后的评判分数之间存在的线性关系。

$R=\left[\begin{array}{cccc}{r}_{11}& z_{12}& \mathrm{...}& z_{1p}\\ r_{21}& z_{22}& \mathrm{...}& z_{2p}\\ ⋮& ⋮& ⋮& ⋮\\ r_{p1}& z_{p2}& \mathrm{...}& z_{pp}\end{array}\right]$ (6)

其中

$r_{ij}=\frac{{\displaystyle \underset{k=1}{\overset{n}{\sum }}\left(x_{ki}-{\bar{x}}_i\right)\left(x_{kj}-{\bar{x}}_j\right)}}{\sqrt{{\displaystyle \underset{k=1}{\overset{n}{\sum }}{\left(x_{ki}-{\bar{x}}_i\right)}^2{\displaystyle \underset{k=1}{\overset{n}{\sum }}{\left(x_{kj}-{\bar{x}}_j\right)}^2}}}}$ (7)

其意义为原变量之间 $x_1,x_2,\cdots ,x_7$ 之间的相关系数。

Step 2 计算各个主成分的贡献率

先计算相关系数矩阵R的特征值和特征向量，然后进一步求得各主成分的贡献率以及累计贡献率。下面以男性为例，如表3所示，可以发现选取5个主成分为男会员的综合评分标准比较合适，总贡献率接近80%。同样的，取5个主成分后，女性的总贡献率在84%左右。同时通过KMO球形检验，两组数据的取样适当性都在0.5左右，比较合适进行主成分分析。男性女性年龄分段量化表见表7。

Table 7. Male membership feature values and principal component contribution table

表7. 男会员特征值及主成分贡献率表

Step 3 计算主成分负荷

主成分载荷由原始变量，即会员的七项指标 $x_1,x_2,\cdots ,x_7$ 按照不同的权重求和得到，选取五个主成分就会得到5个主成分负荷，根据求得这些主成分负荷时七项原始指标权重的不同，这5个主成分负荷所代表的意义在不同的指标也有所侧重。当分别男女会员的数据进行处理计算主成负荷分时，由于各原始指标的权重有所不同，所以可得到两组不同的主成分负荷：男性女性会员主成分负荷Y。

$Y=\left[\begin{array}{lllll}{Y}_1\hfill & Y_2\hfill & Y_3\hfill & Y_4\hfill & Y_5\hfill \end{array}\right]$ (8)

由于我们对男性会员和女性会员的数据分别进行主成分分析，所以会产生两套以上提及的变量，我们用下标加以区分，1代表女性，2代表男性。

$Y_1=X_1{E}_1$ (9)

$Y_2=X_2{E}_2$ (10)

要求得Y的实际值，需要先确定原始指标的各项权重，即成分的得分矩阵E，该矩阵由spss处理给出：

$E_1=\left[\begin{array}{lllll}0.57\hfill & 0.11\hfill & 0.29\hfill & 0.17\hfill & 0.09\hfill \\ -0.28\hfill & 0.52\hfill & 0.13\hfill & 0.37\hfill & -0.62\hfill \\ 0.53\hfill & 0.20\hfill & 0.38\hfill & 0.15\hfill & -0.15\hfill \\ 0.37\hfill & 0.42\hfill & -0.28\hfill & -0.28\hfill & 0.26\hfill \\ -0.29\hfill & -0.10\hfill & 0.75\hfill & 0.06\hfill & 0.42\hfill \\ -0.24\hfill & 0.55\hfill & -0.19\hfill & 0.38\hfill & 0.57\hfill \\ -0.19\hfill & 0.43\hfill & 0.27\hfill & -0.76\hfill & -0.09\hfill \end{array}\right]E_2=\left[\begin{array}{lllll}0.70\hfill & -0.04\hfill & 0.09\hfill & 0.21\hfill & 0.01\hfill \\ 0.07\hfill & 0.21\hfill & 0.44\hfill & -0.79\hfill & -0.33\hfill \\ 0.70\hfill & -0.14\hfill & 0.01\hfill & -0.11\hfill & -0.08\hfill \\ 0.05\hfill & 0.61\hfill & 0.09\hfill & -0.11\hfill & 0.68\hfill \\ -0.14\hfill & -0.33\hfill & 0.57\hfill & 0.06\hfill & 0.53\hfill \\ 0.05\hfill & 0.67\hfill & 0.04\hfill & 0.35\hfill & -0.22\hfill \\ -0.04\hfill & 0.02\hfill & 0.68\hfill & 0.42\hfill & -0.31\hfill \end{array}\right]$

定义原七项指标为向量X：

$X_1=\left[\begin{array}{lllllll}{x}_{11}\hfill & x_{12}\hfill & x_{13}\hfill & x_{14}\hfill & x_{15}\hfill & x_{16}\hfill & x_{17}\hfill \end{array}\right]$ (11)

$X_2=\left[\begin{array}{lllllll}{x}_{21}\hfill & x_{22}\hfill & x_{23}\hfill & x_{24}\hfill & x_{25}\hfill & x_{26}\hfill & x_{27}\hfill \end{array}\right]$ (12)

Step 4 得出综合评价系数

在上图中，通过表3中的贡献率可以得出综合评价公式 = 各个贡献率*各个对应的主成分，我们将男会员和女会员的综合评价得分分别记为P₁，P₂。结合step3得出公式：

$P_1=0.28726\times Y_{11}+0.20462\times Y_{12}+0.15171\times Y_{13}+0.12612\times Y_{14}+0.0934\times Y_{15}$ (13)

$P_2=0.19961\times Y_{21}+0.16754\times Y_{22}+0.16299\times Y_{23}+0.13875\times Y_{24}+0.13043\times Y_{25}$ (14)

分别带入P₁，P₂公式，我们就可以得出最后的评判分数，并且筛选出按照我们制定的标准出来的优质男会员和女会员。

6.3.3. 结果分析与验证

在进行主成分分析后，得出了优质男会员和优质女会员的前20名(详见附录)。从女会员角度看，所入选的女会员的年龄和学历的比重比较大，而它的收入情况，占的比重，不是特别大。而对于所入选的优质的男会员来说，其身高和收入，所占的权重比较大，这也比较符合现实状况。为了衡量所打分数的合理性，我们以会员样本数为横轴，纵坐标为打分情况见图12、见图13所示。

Figure 12. Distribution of quality male members

图12. 优质男会员分布图

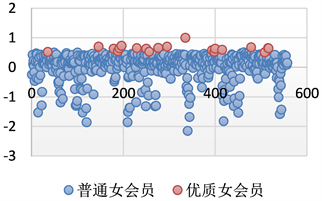
Figure 13. Distribution of quality female members

图13. 优质女会员分布图

从上图气泡的分布情况来看，根据主成分分析法打出的人评分，在各个分数段均有分布，分布总体呈现比较均匀的趋势，能够比较良好的反应，这一整个打分系统的稳定性和可信度。从图中显示的优质男会员和优质女会员的分布来看，分布在样本数据的各个层次，并没有出现数据吞食的状况。虽然该数据成分没有考虑到地区的因素，但是他比较有针对性的，针对男会员和女会员的区别，做出了相对良好的筛选。在评分过程中存在出现负分的现象，虽然在实际意义中并没有真实的价值。但是该副职只是表明该会员的各个条件相比于其他会员来说较差。通过分布图，我们可以发现，对于打分比较低的会员，在整个样本中所占取的数量相对较少，这也再次印证了利用主成分分析法对男女会员进行甄别的方法是可行的 [5]。

6.3.4. 模型灵敏度分析

除了上述验证该系统的合理性外，还需要引进更加合理的参数对这个系统进行评价，这里我们采用云模型，对我们建立的模型进行灵敏度分析。

云模型通过期望，熵，超熵三个量表示该数据的特征。通过对已知数据生成足够的云堤和计算这些云低的数字特征来评判，这些数据的确定度，从而验证该数据的水平度。

在这里我们分别把女会员和男会员的评判得分随机的抽取相同的值代入云模型，进行灵敏度分析，得到如图14、图15所示的两个评分模型还原图。女性见图14，男性见图15。

Figure 14. Females

图14. 女性

Figure 15. Male

图15. 男性

通过对女生和男生的评判模型还原图，我们可以发现，绝大多数的评分，其确定度均高于0.6，符合合理数据的分布规律。在女会员和男会员的确定度为0.8到1的这些数据中，占据了整个评判的绝大部分。同时该模型的离散程度也较强。因此该模型的灵敏度较为良好，可以比较准确客观的反映出所选优质会员的程度。

7. 模型的评价与推广

7.1. 模型的评价

7.1.1. 模型的优点

1) 在求解第一问时，我们运用两种方法分别对身高差值上下限和期待对象收入确实数据进行填补，即最小绝对残差法和线性插值法。因为在挑选对象身高时，会员会结合自身身高作为参考，所以运用两种方法填补数据比较符合实际，得出结果更加细致准确。

2) 在求解第二问时，我们运用的是字符串长度匹配的方法，这是一种古老的、研究广泛的计算机匹配算法。运用Python编程，当一个会员的自身条件与另一个会员期待的条件相似度最大时，即可认为满意度最大，这种方法运用起来简单。

3) 在求解第三问时，我们结合实际情况，优质男女会员的评价指标不尽相同，比如年龄在评价优质女会员时占较大比重。于是我们运用主成分分析方法将男女会员数据分别进行分析得到各自的主成分，这样评价较为客观。

7.1.2. 模型的缺点

在求解问题二时，我们运用的字符串匹配算法在处理离散特征数据的时候，数值型字符串在进行计算时往往会产生偏差。在求解问题三时，我们对会员所在单位类型的量化没有确定的指标，比如国有企业、私营企业、事业单位、政府机关等，我们对其随机编码量化。并且，我们没有将会员所在地区考虑进来，这可能会对评价的准确性产生一定影响。

8. 结束语

本文是基于互联网时代相亲配对建立的数学模型，该模型可以在众多前来相亲的会员中选出优质男女会员，并且可以实现计算机自动配对使得男女会员的满意度达到最大。这样一来，婚恋网就可以根据该数据为会员介绍对象，至于以后发展如何，就看双方在交往后的意愿了。该模型具有通用性，除了相亲配对外，还可以运用在其他的配对案例中比如职工分组，研究生填报志愿等。