1. 引言
中空纤维膜组件是膜生物反应器的基本组成结构之一 [1] 。本文使用Fluent软件建立了单根中空纤维式渗透汽化膜丝管的CFD模型,并对建立的单根中空纤维膜CFD模型进行轴向仿真,分析研究膜通量分布特性并研究影响单根中空纤维膜丝管能源使用效率的因素。由于膜组件的压降较大,因此采用气液两相混合进料进行模拟,气液两相进料模拟能够高效地减少中空纤维式渗透汽化膜内部压强,促进管流湍动,削弱壁面处所形成的浓度差和温度差极化层,增大传质效果。膜内的流体发生渗透汽化时,有一部分会在组分溶解扩散透过膜时耗热,另外有一部分,在透过层时会蒸发,从而有一定的耗热,大多数流体会在经过这两种情况后造成自身温度的损耗,但是如果采用气液两相混合进料进行模拟,因为有气体可以产生这部分所必须的热量,所以不需要液体损耗自身热量。本文研究的膜生物反应器以天津某公司的产品为研究对象,首先附上某种8英寸膜的性能参数,如表1所示。

Table 1. UOF-4 type membrane module performance parameters table
表1. UOF-4型膜组件性能参数表
Continued
2. 基于CFD方法和Fluent软件的单根中空纤维膜丝管模型
2.1. 单根中空纤维膜丝管的模型建立、网格划分和边界条件设置
如图1表示使用ICEM CFD前处理器所建立的单根中空纤维式渗透汽化膜丝管的几何模型,由于本文中膜丝管的运行方式是外压式的,所以当MBR系统运行时,污水从管壁侧面的微孔流入,而污水中的杂质从膜丝管的两端流出,这样就达到了过滤污水的效果了。
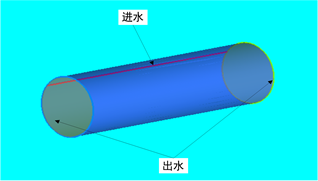
Figure 1. Geometric model of single hollow fiber membrane filament
图1. 单根中空纤维膜丝几何模型
因为在FLUENT求解器计算网格文件时是以网格为单位元进行计算的,所以接下来对该几何模型进行网格划分,在ICEM CFD中网格划分有结构化网格划分和非结构化网格划分两种 [2] ,这里因为中空纤维管的质量分布均匀,所以我们采用结构化网格划分方法 [3] ,其中对圆形部分采用O型切分。如图2所示的网格文件是我们最终的划分结果,如图3所示为网格质量图,网格质量的高低会影响求解器的计算,如果网格质量太低的话,那么在求解器中会出现不收敛的情况,一般来说网格质量越接近于1说明网格质量越好,从图3中我们能观察到最小网格质量是0.733,所以该模型的网格质量基本符合要求。

Figure 2. Single filamentous mesh file
图2. 单根膜丝的网格文件
2.2. FLUENT求解器对单根中空纤维膜丝管模型网格文件的计算
将网格文件导入FLUENT求解器,首先检查网格质量,保证最小体积不为负数,然后开始准备设置初始条件等预处理操作。这里我们选择基于压力稳态的求解器 [4] ,并设置重力加速度−9.8。因为这里水的流速较低,所以我们选择层流模型 [5] 。然后我们导入流体材料,由于这里讨论的是中空纤维膜纯水过滤研究,所以我们只导入水这种材料即可,之后设置流体区域并打开多空介质模型。最后设置进出口边界条件,这里我们设置速度为入口边界条件,出口边界条件为压力出口,到这里为止设置初始条件等预处理操作基本完成,下面选择求解算法进行求解计算。
这里算法我们选择压力-速度耦合算法模型 [6] ,其中梯度我们选择基于单元体的最小二乘法,压力选择迭代法,动量方程选择一阶迎风格式的。然后设置残差阈值并初始化,最后设置最大迭代次数500次,开始计算。图4所示为求解器计算的残差曲线图,残差在数理统计中是指实际观察值与估计值(拟合值)之间的差,其中红色、绿色和黄色的残差曲线分别代表三维空间中x、y、z三个方向的速度残差情况,白色残差曲线代表求解器连续性情况,随着它们的残差减小,则求解器的计算结果就越精确,我们可以将残差看作误差的观测值。从图中我们不难发现当迭代到32次时求解器达到收敛自动停计算,即求解结束。
3. 仿真结果及分析
我们假设当二维管道的管壁流动时,膜通量在中空纤维反渗透膜组件中的扩散是整体均匀的。由于要考虑到壳侧的空隙率,因此管与壳侧之间0.356 mm厚的多孔膜面积不可忽略。同时,利用微扰法研究管壁雷诺数较小的二维通道内的流体流动 [7] ,我们知道如果管壁雷诺数比较小,流体的活动基本不受渗透的干扰,通道内的流动特性接近HaGe-Poisson流。本文中,管壁雷诺数总是0.08的量级中心,所以可以保证所求轴向速度分布曲线的正确性。但是,管壁雷诺数不能完全决定管壳轴向速度分布,依此来判定的速度分布会出现一定的误差,影响轴向速度的另一个重要因素是渗透率 [8] ,所以,如果要完全获取截面的上游和下游的轴向分布,就必须匹配上液面和管壁上相对应的渗透率。
考虑到H型壳侧空隙的CFD模拟和分析模型获得的沿膜丝长度的流量分布不均匀性,图5所示为局部通量仿真图,任何局部通量的相对偏差应在±12%之内,并且壳侧的空隙率为0.35。通量分布在0.7和0.9的平均偏差分别为1.67%和1.25%。
图6和图7所示为单根纤维膜丝管内部的轴向仿真示意图,从左至右,当膜丝的渗透系数从4.00x15-i3_m2增加至4.12xl5-i6_m2时,能量利用率由87.0%下降到52.0%,膜阻力加大时,膜渗透系数会降低,膜丝渗透分布的不均匀性会影响到膜丝管的通量分布特性,即膜分布越均匀,通量分布越均匀,通量分布越均匀,则单根中空纤维膜丝管的能源使用效率越高。
4. 结论
本文利用Fluent软件建立了单根中空纤维膜丝管的仿真模型,划分了仿真模型的网格,设置了模型的边界条件。轴向仿真了单根中空纤维膜丝管CFD模型,分析研究了膜丝管的膜通量分布特性,仿真结果证实,当加大膜丝管内某一部分的膜通量时,该部位膜丝的高通透指数也会增加,从而使单根中空纤维膜丝管产生贯穿整体的跨膜压差,这一压强差会导致膜丝管通量的不均匀分布,膜通量的不均匀分布会导致膜丝管的通透性降低,从而影响单根中空纤维膜丝管的能源使用效率。
基金项目
国家自然科学基金(51378350);国家青年科学基金(50808130)。
NOTES
*通讯作者。