基于边缘检测和聚类分析的浅剖图像分层算法

A New Method of Classification on Shallow Sub-Bottom Profiles Based on Image Edge Detection and Cluster Analysis

摘要: 本文提出了一种基于边缘检测和聚类分析的浅剖图像分层算法。利用自适应的Canny边缘检测算法有效提取了图像边缘，利用区域跟踪算法，确定了二值图像中所有目标的边界，根据k-means聚类分析算法，对多条边界进行了有效分类，实现了地层划分。以钻孔数据为参考，比较了基于边缘检测和聚类分析的浅剖图像分层算法与ISE软件处理结果的精度。结果表明，本文提出的方法在海底高程和三个层底高程的识别中，中误差为0.47米，远小于ISE的1.37米，说明该方法优于ISE处理的结果，可以为处理浅地层剖面图像提供一个新的思路和方法。

Abstract: A new method of classification on shallow sub-bottom profiles based on edge detection and cluster analysis is presented in the paper. The sub-bottom profile image edge is effectively extracted by Canny edge detection algorithm, and image boundaries of all objects in binary image are deter-mined by region tracking algorithm. According to the k-means clustering algorithm, effective clas-sification of boundary and the stratigraphic division are realized in this paper. Taking drill hole data for reference, the results from the paper’s algorithm and ISE software are compared. The re-sults show that the error of mean square is 0.47 meters according to the proposed method, far less than 1.37 meters of ISE. Therefore the method is superior to the ISE processing results and can provide a new idea and method for the treatment of shallow profile image.

1. 引言

浅地层剖面仪应用声学原理可以有效地获取海底沉积物的分布、地质结构等相关信息，由于其具有连续走航式探测、作业方便、成本低、效率高、探测分辨率高以及穿透深度大并能获得与地质剖面相似的记录图谱等优点，在海洋工程调查和海洋地质研究中得到了广泛的应用 [1] [2] [3] [4] [5] 。虽然，野外工作获得的浅地层剖面图谱已经能够反映海底地质构造的一些特点，但是海底下伏地层岩土类型、分布和结构非常复杂，并且浅地层剖面仪所基于的声学方法和技术也具有一定的局限性，导致了诸如非自激自收导致的地层厚度畸变、特殊反射界面导致的空间变形以及地层中声速变化导致浅地层剖面地层失真等诸多问题，使观测数据质量大幅降低，严重影响剖面的解释，甚至造成地层界面模糊不清而无法进行解释 [6] [7] [8] [9] [10] 。而在资料后处理和解释方面，大都根据经验，采取人工或浅剖软件自动分层的方式对海底浅剖图像进行分层，由于浅剖图像的复杂性，导致了人工和相关软件无法正确地对地层进行有效识别，致使其高分辨率的潜在优势无法得到更好的利用。而浅剖图像作为一种图像，也具有纹理和边缘等基本图像的特征 [11] [12] [13] 。

在图像边缘检测中，传统的边缘检测算子是依据图像的每个像素邻域内灰度值的变化，采用数学方法中的一阶或二阶方向导数的变化来检测边缘。这些算子结构简单，实现速度较快，但是对噪声影响较大，Canny算子基于最优化算法的边缘检测算子，该算子在处理高斯白噪声污染的图像方面优于其他传统的边缘检测算子，因而得到广泛应用 [14] [15] [16] 。

本文利用Canny算子对浅剖图像进行了边缘检测，然后利用区域跟踪算法检测出的图像边缘，给出二值图像中所有目标的外边界和内边界，最后利用k-means聚类分析对边界进行分类，根据分类的结果确定了各层边界，并与ISE软件分层结果和钻孔数据进行了对比，得到一些有益的结论。

2. Canny边缘检测

Canny算子的基本思想是采用二维高斯函数的任意方向上的一阶方向导数为噪声滤波器，通过与图像卷积进行滤波，然后对滤波后的图像寻找局部梯度最大值，并以此来确定图像的边缘 [17] 。

1) 用高斯滤波平滑图像。

Cammy算法选用一维高斯函数，分别按行和列对图像进行平滑去噪。所选高斯函数为：

$G\left(x\right)=\frac{1}{\sqrt{2\text{π}}\sigma }{e}^{\frac{-x^2}{2{\sigma }^2}}$ (1)

式中， $\sigma$ 为高斯曲线标准差。

2) 用一阶偏导有限差分计算图像的梯度幅值方向。

Cammy算法采用2 × 2邻域一阶偏导的有限差分计算平滑后的数据阵列 $I\left(x,y\right)$ 的梯度幅值和梯度方向。和 $y$ 方向偏导数的2个阵列 $P_x\left[i,j\right]$ 和 $P_y\left[i,j\right]$ 分别是

$P_x\left[i,j\right]=\left(I\left[i,j+1\right]-I\left[i,j\right]+I\left[i+1,j+1\right]-I\left[i+1,j\right]\right)/2$ (2)

$P_y\left[i,j\right]=\left(I\left[i,j\right]-I\left[i+1,j\right]+I\left[i,j+1\right]-I\left[i+1,j+1\right]\right)/2$ (3)

像素的梯度幅值和梯度方向用直角坐标到极坐标的坐标转换公式计算，用二阶范数来计算梯度幅值为：

(4)

梯度方向为：

$\theta \left[i,j\right]=\arctan \left(P_y\left[i,j\right]/P_x\left[i,j\right]\right)$ (5)

3) 对梯度幅值进行非极大值抑制，保留局部梯度值最大的点。

为了提取单像素边缘，必须细化梯度幅值图。在梯度幅值图像中， $M\left[i,j\right]$ 的极大值所在位置附近会产生屋脊带，只有细化这些屋脊带才能精确的确定边缘的位置，只保留幅值局部变化最大的点。在非极大值抑制过程中，Cammy算法使用3 × 3大小，包含8方向的邻域对梯度幅值阵列 $M\left[i,j\right]$ 的所有像素沿梯度方向进行梯度幅值的插值。在每个点上，邻域的中心像素 $m\left[i,j\right]$ 与沿梯度方向的2个梯度幅值的插值结果进行比较，如果邻域中心点的幅值 $M\left[i,j\right]$ 不比梯度方向上的2个插值结果大，则将 $m\left[i,j\right]$ 对应的边缘标志位赋值为0，这一过程把 $M\left[i,j\right]$ 宽屋脊带细化为一个像素带，并且保留了屋脊的梯度幅值。

4) 用滞后阈值检测并连接边缘。

Cammy算法利用双阈值算法对非极大值抑制图像进行两次阈值分割，得到低阈值图像 $N_1\left(x,y\right)$ 和高阈值图像 $N_2\left(x,y\right)$ 。由于 $N_2\left(x,y\right)$ 由高阈值得到，因而含有很少的假边缘，但有间断，于是就在 $N_1\left(x,y\right)$ 的8邻域位置不断收集边缘，直到将 $N_2\left(x,y\right)$ 连接起来。

3. 浅剖图像的边缘和边界检测

在绘制地层线时，可以采用自动跟踪和手动绘制两种方法。自动跟踪是利用浅地层剖面仪配套的处理软件进行跟踪。而地层线在自动追踪后，即使进行了平滑处理，差异非常大，显得参差不齐。特别是当海域沉积环境复杂，在这样的情况下使用自动追踪，是不能完成地层划分的。因此，在复杂地层线的绘制中，主要采用的是手动绘制地层线，这样有利于清晰的反映地层的分界，有利于地层划分工作。然而人工划分地层受人为因素影响较大，且效率比较低。

浅地层剖面图像是反映海平面变化，在冲积平原或近岸环境中反映沉积环境的变迁过程。剖面声图显示的具有一定灰度的点状、块状和线状图形组成的图像层理，反映了不同性质的海底浅部地层特征。

图1是浅地层剖面仪的彩色图像，从图像中可以看出，每次信号的变化都对应着一层强声学反射层。从图1可以看出，图像是由S型的线状和块状图形组合而成的S型复杂层理，通常表示三角洲及浅海环境，沉积物粒度从细到粗的沉积序列。同时，图1还包括了由不连续、不整合的点状图形组合的杂乱层理，表示高能量沉积环境，反映了沉积后基底瓦解，崩积后残、堆积等沉积过程。另外，从图1中还可以看到，图像中存在没有灰度的点状、块状和线状图形，几乎是一片空白带或干扰图像，即无声反射带。在灰度图像(图2)中，各地层图像像素的灰度值变化不明显，其特征与原始彩色图像基本一致。

Figure 1. Original image of the sub-bottom profile

图1. 浅剖原始图像

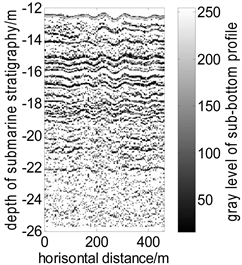
Figure 2. Gray-scale image of the sub-bottom profile

图2. 浅剖灰度图像

利用Canny边缘检测方法对灰度图像进行了边缘检测。在边缘检测中，利用平滑后的图像梯度幅值矩阵，寻找图像中可能的边缘点，然后利用双门限检测通过双阈值递归寻找图像边缘点，实现了边缘提取。在Canny边缘检测时，高斯滤波参数和高低阈值的选取通常采用人工的方式设定，为减少人为因素的影响，本文采用了自适应的Canny边缘检测算法，得到了高低阈值和平滑参数分别为0.6、0.3和1.3。如图3所示，提取的图像边缘由多条长短不一的点状和线状图形组成。

为了获取二值图中对象的轮廓，包括外部轮廓与内部边缘，采用了区域跟踪算法，确定了二值图像中所有目标的外边界和内边界。通过区域跟踪，一些连通的闭合的边缘像素被确定为边界，如图4所示。在图4中，图像多个部分都包含一些边界，其中，红色区域表示较好的连通性，表明该区域的地层反射强度较强。对于识别出的各个边界是否属于同一类别，需要进行聚类分析。本文利用了k-means聚类分析的算法，对多条边界进行了分类。

Figure 3. Canny edge detection

图3. Canny边缘检测

Figure 4. Edges detected by the region tracking algorithm

图4. 区域跟踪识别的边界

4. K-means聚类分析

k-means是基于划分的聚类算法。该算法简单、快速，是一种得到最广泛使用的聚类算法 [18] 。k-means以k为参数，把n个对象分为k个类别，以使类内具有较高的相似度、类间的相似度较低。根据一个类别中对象的平均值进行相似度的计算，对大数据集的处理，该算法是相对可伸缩和高效率的 [19] 。

k-means使用迭代的方式在各聚类内最小化到聚类中心的距离和，迭代过程中算法在聚类间不断改变点的归属直到距离和不再减小，最终得到一组紧凑、分类良好的聚类。为了查看分类效果的好坏，可以绘制输出结果聚类切片的轮廓图。轮廓图用来衡量一个聚类中的点与相邻聚类中点的接近程度。返回的silhouette值在−1~1之间，1表示点离其他聚类很远，0表示点离另一个类很近，−1表示点可能被赋错了类，平均silhouette值越大，表明分类结果越理想 [20] 。本文利用k-means算法对图像边界分别进行了2、3、4和5个类别的聚类分析，聚类的结果如图5(a)、5(b)、5(c)和5(d)所示。

从图5可以看出，在(a)的第2类，(c)的第1类和(d)的第4和第5类中，均有负值存在，说明(a)、(c)和(d)三个图的部分边界点可能被分错了类。而(a)、(b)、(c)和(d)的平均silhouette值分别为0.6005、0.6732、0.5419和0.5319，(b)的分类结果的平均silhouette值最大，且没有负值出现，说明对于浅剖图像的边界分为3类是最为合理的。利用k-means算法对图像的边界分为三类的结果如图6所示。

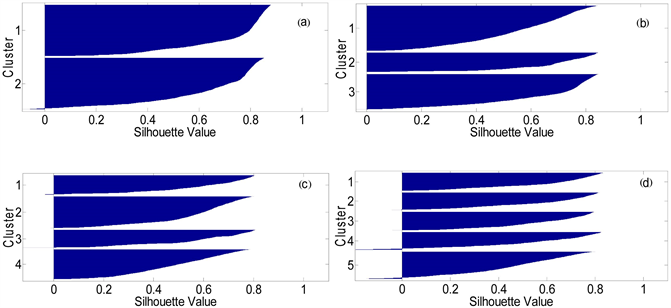
Figure 5. The clustering results of k-means

图5. K-means聚类分析结果

Figure 6. K-means clustering results of the submarine strata

图6. 海底各地层的k-means聚类结果

从图6中可以看出，该海域的浅剖图像被分为了三类，即三个主要地层。根据最靠近各类边缘的边界，本文利用最小二乘进行了拟合，拟合的直线如图6所示。由此可见，各地层被拟合的边界直线进行了划分，从而实现了浅剖图像各地层的自动划分。

5. 对比与分析

本文利用ISE软件对浅地层剖面图像进行了分层处理。通过进行相关设置，过滤了水体上部的噪声，再从地层附件开始跟踪水底线，设置完成后，软件会自动跟踪出水深线，然后跟踪地质分层线，即可计算各个地质分层，ISE软件分层处理的结果如图7 (红线)所示。为了比较本文采用的分层方法与现有浅剖图像处理的常用ISE软件的优劣性，本文以钻孔数据为参考(如图8所示)，比较了本文划分的地层与ISE软件的划分结果。

由钻孔数据分析可知，该海底地层中，海底高程为−11.7米。第一层为粉土，黄褐色–灰褐色，饱和，中密，局部稍密，具层理，上层部分含较多粉砂薄层，局部夹粘性土薄层，含粘性团块，夹灰黑色条带，土质均匀性较差，第一层层底高程为−15.8米。

Figure 7. ISE software stratification

图7. ISE软件分层

Figure 8. Drilling histogram

图8. 钻孔柱状图

第二层为淤泥质粉质粘土，局部出露为粉质粘土，黄褐色为主，局部为灰褐色，颗粒细腻，切面光滑，局部夹粉土薄层并含粉砂颗粒，偶含粉砂颗粒，夹灰黑色条带及灰色斑块，第二层层底高程为−18.7米。

第三层为粉土，灰褐色，饱和，中密，具层理，土质均匀性差，含较多粘性土，第三层层底高程为−21.7米。

本文比较了几种方法的分层结果，如表1所示。

Table 1. Comparison of different methods (unit: m)

表1. 各种方法分层结果对比(单位：m)

从表1中可以看出，ISE软件能够实现自动分层，但在与钻孔数据的对比中，除海底高程与钻孔数据差异较小外，其余各层高程与钻孔数据相差较大，最大为第二层层底高程，相差3.7米，一方面与该海域地层复杂有关，另外，在实际的处理中，人为干预的因素也是一个重要影响因素。而本文采用的分层方法与钻孔数据对比，最大为海底高程，相差1米，最小为第一层层底高程，仅相差0.1米。利用与钻孔数据的差值计算的中误差，ISE软件为1.37米，而本文采用的方法计算的中误差为0.47米，远远小于ISE，因此，本文采用方法的精度明显高于ISE软件分层结果。

6. 结论

本文对浅地层剖面图像进行了图像处理，利用自适应的Canny边缘检测算法有效提取了图像边缘；通过区域跟踪算法，确定了二值图像中所有目标的外边界和内边界。利用了k-means聚类分析算法，对多条边界进行了分类。以钻孔数据为参考，比较了本文提出的方法与ISE软件处理结果的精度。结果表明，本文提出的方法在海底高程和三个层底高程的识别中，中误差为0.47米，远小于ISE的1.37米，说明本文提出的方法优于ISE处理的结果，可以为处理浅地层剖面图像提供一个新的思路和方法。

NOTES

^*第一作者。