1. 引言
数据挖掘是知识发现的一个步骤,是从大量的、不完全的、有噪声的、模糊的、随机的数据中,提取出隐含在其中的、人们事先不知道的、但又是潜在有用的信息和知识的过程[1]。分类规则挖掘是数据挖掘领域中最重要的研究领域之一,同时,也是其它诸如人工智能、模式识别、人工神经网络等学科的重要研究内容,并且有丰富的结果和广泛的应用,因此对分类规则挖掘的研究是很有必要的[2]。
Morse理论最初是由Marton Morse在其论文中提出的,通过分析黎曼流形上Morse函数的临界点来研究流形的拓扑结构,是一种非常有用的优化工具。随后,Forman在Morse理论的基础上进行了进一步的研究,并将离散结构引入Morse理论中,形成了离散Morse方法本文又将离散Morse方法延伸到狭义离散Morse方法,并以此来解决分类规则挖掘问题。
2. 相关理论
根据参考文献[3-5],下面给出几个关于离散Morse方法的概念描述:
定义1 单元:p维单元α(p)是一个同胚于开放的p维球体: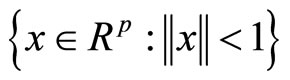 。当单元的维度p很明显的时候,我们可以用α来代替α(p)。
。当单元的维度p很明显的时候,我们可以用α来代替α(p)。
定义2 CW-复形:零维单元K0是一个点,沿着它的边界连接一维单元线段,得到K1,沿着K1的边界连接二维单元面(如三角形),得到K2,沿着K1边界连接三位单元体(如正方体),得到K3,依次类推下去,就可得到每一个n维单元Kn。这些单元组成的离散集合就建立了一个CW-复形。如果单元的个数是有限的,则我们就说CW-复形是有限的。
定义3 Hasse图:Hasse图是通过结点的维数来确定结点的队列安排的。
单纯复形K的Hasse图是满足以下条件:
1) H的每个结点代表H的一个单元。
2) H结点间的链接代表K的相关单元。
3) 每个链接的根结点是单纯复形K中的最高维单元。
定义4 离散Morse方法:函数f:K→R是单纯复形K上每个单元到全体实数的一个映射,对任意单元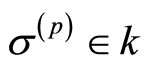 ,如果满足以下条件:
,如果满足以下条件:
#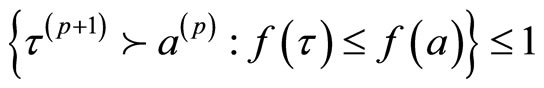
且
#
则函数f就叫做单纯复形K上的离散Morse函数。
定义5 组合梯度向量域:单纯复形K上的组合梯度向量域是相关单元 的一个不相交的集合。我们可以把离散梯度向量域定义成函数V:
的一个不相交的集合。我们可以把离散梯度向量域定义成函数V: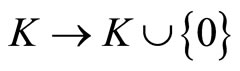 ,且满足
,且满足
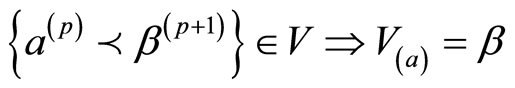
且
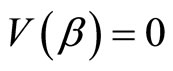 。
。
从单元α到单元β画一个箭头来表示这个配对。如果单元σ不属于任何配对,则V(σ) = 0。
定义6 V-路径:单元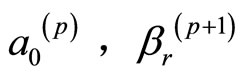 ,
,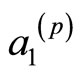 ,
,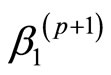 ,……,
,……,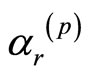 ,
,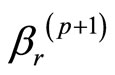 满足
满足
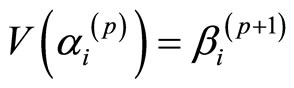
且
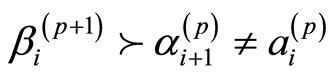
则这样的单元构成的交替序列叫做V-路径。
定义7 离散梯度向量域:如果当 时满足
时满足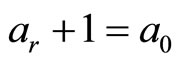 ,则V-路径是非平凡且闭合的。不存在非平凡且闭合的V-路径的组合向量域叫做离散梯度向量域。
,则V-路径是非平凡且闭合的。不存在非平凡且闭合的V-路径的组合向量域叫做离散梯度向量域。
定义8 广义的离散Morse函数:为一个单纯复形K的每个单元都映射一个实数函数f:K→R,如果对每一个p维单元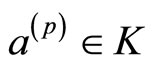 ,它都满足:
,它都满足:
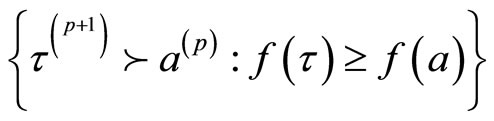
且
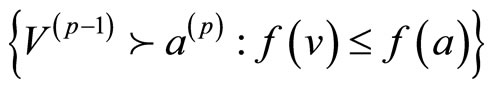
那么函数f是一个定义在单纯复形K上的广义离散Morse函数。
定义9 广义离散梯度向量域:在一个单纯复形中,如果存在单元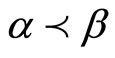 ,有
,有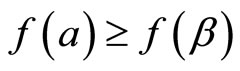 ,则在α、β之间画一个箭头,其中α是箭头的尾,β是箭头的头,这样形成的梯度域称为广义离散梯度。单元α可以是多个箭头的尾。
,则在α、β之间画一个箭头,其中α是箭头的尾,β是箭头的头,这样形成的梯度域称为广义离散梯度。单元α可以是多个箭头的尾。
3. 算法步骤
在参考文献[6]中给出了构建离散Morse函数和构建离散梯度向量域的方法,本文将给出详细的构建离散Morse函数和构建离散梯度向量域的算法步骤。
3.1. 超树和超图
超图是一个配对(N, L),其中N表示图中所有的结点的集合,L表示跟N相关的所有关联。L中的元素称为超链。规则超链指的是只跟两不同结点相关的链接。只与一个结点相关的链接是环。而非规则超链是指环和同时跟三个或以上的结点相关的链接。
如果一个简单有向超图的每个结点至多是一个超链的根,并且不包含任何超环。则称其为超树。
T. Lewiner在文献[7]中已证明:超树HF的任一规则部分R要满足下面的条件:
1) HF的规则部分R是简单树。
2) R中至多有一个结点是环或者是非规则部分的超链接。
对于超树,如果它的规则成分中不存在与根结点相关的环或不规则超链,则称之为临界部分。
3.2. Hasse图、离散Morse函数及离散Morse 向量域之间的关系
对于每个离散Morse函数,总存在一个离散梯度向量域同其有相同临界单元,而对每个离散梯度向量域,也存在一个有相同临界单元的离散Morse函数。故构建离散梯度向量域也就是构造相应的离散Morse函数。构造离散Morse函数和离散梯度向量域需要用到Hasse编码,事实上,离散梯度向量域的配对跟Hasse图中的配对是一一对应的。离散梯度向量域可以看作是从Hasse图中不同层次的超图上提取的超树。
3.3. 离散梯度向量域的构建算法
在单纯复形K上构建生成树ST。为生成树上的所有的结点和链接进行配对,并且确保不在生成树上的结点和链接都处于临界状态。步骤如下:
1) 选取根结点。
2) 在生成树确定一个规则部分R。
3) 如果R为临界部分,则可设任一结点为根结点。
4) 如果R不是临界部分,把叶子结点与其唯一的链接配对。
5) 将R中未配对的结点和链接放到集合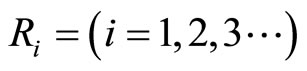 中。
中。
6) 重复4)和5),直到所有链接配对完成。
7) 最后一个结点(未配对)设置为根结点。
生成树的结点表示顶点,生成树的链接表示边。用结点到边的箭头来表示这些配对。由于不存在非平凡闭合的V-路径,所以构建的向量域是离散的。
3.4. 离散Morse函数的构建
在单纯复形K上构建离散Morse函数的步骤如下:
1) 在单纯复形K上构建超树HF。
2) 在HF上选取一个规则部分R,确定规则部分的方法跟构建生成树的方法一致。
3) 如果R是孤立的和超树HF的补集不相关,则为超树HF的结点和链接赋值。
4) 将R的根结点及其相关联的链接赋值为C。
5) 将其它结点赋值为该结点与根结点的距离加C。
6) 两结点间的链接赋值为该两结点中较大者的值。
7) 如果单纯复形K中存在环或者非规则超链接,则为它们赋值为C。
8) 如果R与超树HF的补集相关,则为超树HF补集的结点和链接进行赋值。
9) 重复以上步骤5)、6)和7),直到所有结点和链接被赋值成功。
10) 得到单纯复形K的离散Morse函数f。
4. 利用离散Morse方法构造分类模型
数据挖掘是从大型数据库的数据中提取出人们感兴趣的、隐含的、事先未知的潜在有用信息的知识。分类规则挖掘则是通过对训练样本数据集的学习构造分类规则的过程,是数据挖掘、知识发现的一个重要方面。分类规则挖掘的实质是希望得到高准确性、有趣的和易于理解的分类规则。目前常用的分类规则挖掘方法有决策树方法、统计方法、神经网络方法、粗糙集方法和遗传算法等。而分类规则也可以利用离散Morse方法通过以下方法来进行挖掘。
数据分类是通过挖掘已有的数据训练集,集中同一类数据对象的共同特征,提取分类规则,对整个数据集进行合理分类的过程[8]。分类的目的是能根据已经分类的数据构造出一个分类模型,即分类器。
构造一个分类器,需要有一个样本数据集作为输入。该数据集由一组数据库中记录构成,每条记录与一个特定的类别相对应。通常这些训练样本是之前的一些经验数据。
给定一个有k个类训练数据集D,下面利用离散Morse方法构造一个分类器,来对数据集进行分类。但是得到的结果仍然可能会有相当数量的分类规则是特定用户不感兴趣的。所以仍需根据用户所需进一步对挖掘过程产生的不感兴趣的分类规则进行调整。这可以利用文献[9]中的思路设定支持度度量来实现。当支持度都大于或等于用户事先设定的最小支持度阈值的分类规则才被认为是有趣的。
下面的例子给出训练集D(见表1)。
1) 根据给定的训练数据集,可构造出数据属性的树形结构(如图1)。七个叶子结点分别表示“年龄 ≤ 30”,“年龄为31~40”,“年龄 > 40”,“非学生”,“学生”,“信誉一般”,“信誉良好”,为方便起见,此处我们分别用“L”,“M”,“B”,“N”,“Y”,“F”,“N”来表示它们。中间一层结点表示符合七个叶子结点中的两个条件的购买电脑的情况。最上层结点表示符合七个叶子结点中的三个条件的购买电脑的情况。图中的数字的多少表示顾客购买电脑的可能性大小。
由此可得到一定不购买电脑的类成员:{年龄 ≤ 30,不是学生}属于类{不购买电脑},{年龄 > 40,信誉良好}属于类{不购买电脑}。
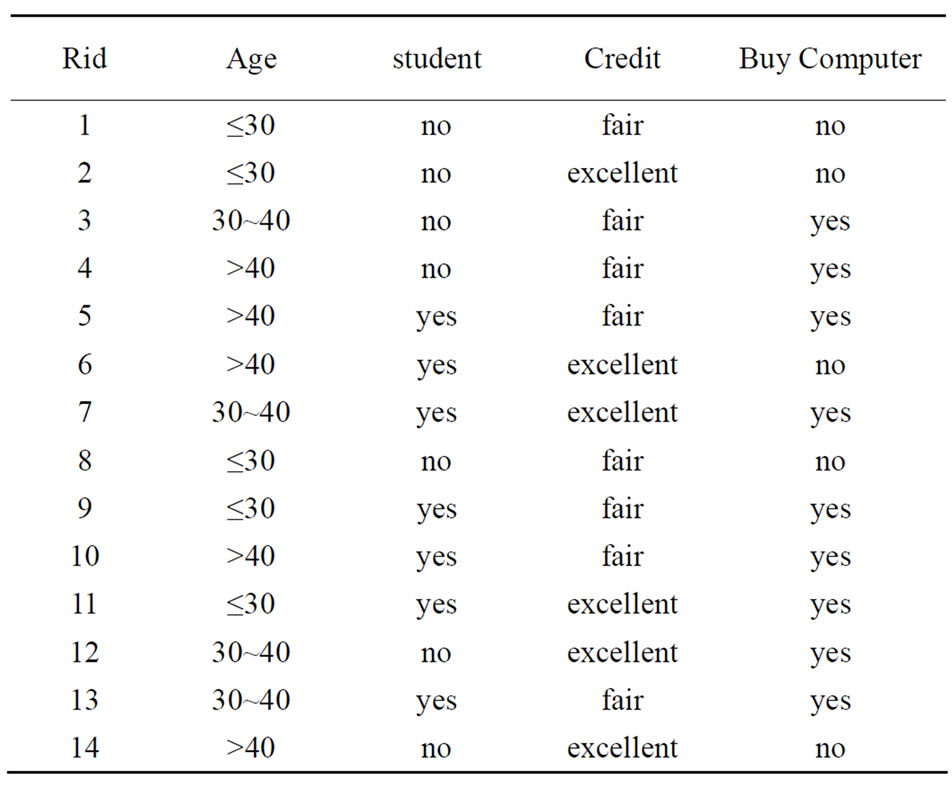
Table 1. One database about customer in a shopping center (training data set)[10]
表1. 一个商场顾客数据库(训练样本数据集合)[10]
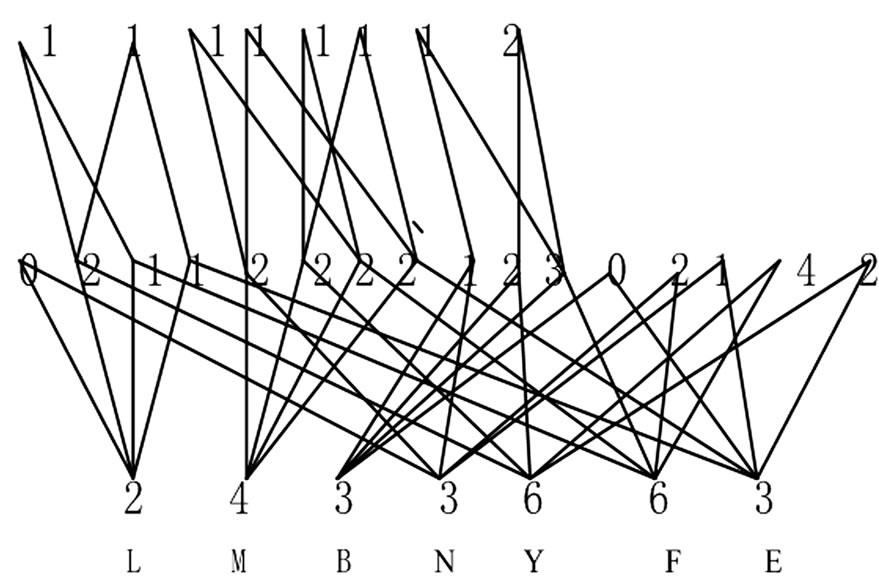
Figure 1. The tree structure of a training data set
图1. 训练数据集的树形结构
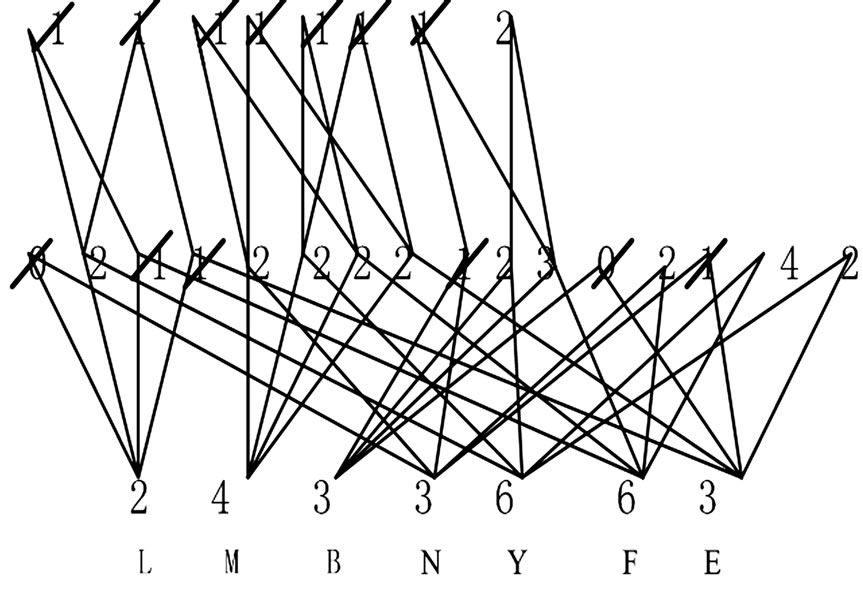
Figure 2. Remove the nodes whose support is less than 2
图2. 删除支持度 < 2的结点
2) 本例中,我们取最小支持度为2,以便使得产生的结果让用户感兴趣。由此可把训练数据集的树形结构的图中支持度小于2的结点删除(如图2),去掉图中多余的链接之后即可得到Hasse图。
3) 由上面得到Hasse图即可以构建一个单纯复形K:一个条件为零维单元(顶点),两个条件为一维单元(线段),……N个条件为N−1维单元。
在单纯复形K中,最高的维数为3,所以它是一个平面图。将Hasse图中每个结点的支持度与单纯复形中的单元权值一一对应起来,即可得到单元带有数值的单纯复形如下图3。
4) 下面我们构造一个用离散Morse函数:a) 在单纯复形的所有单元中选取权值最大者。b) 对所有单元的权值进行修改:用权值最大者减去该单元的权值得到一个新的权值,把新权值赋给该单元。在此例子中,单纯复形中单元最大权值为6,用6减去各个单元的权值可得到如图4的离散Morse函数。
5) 构建与此离散Morse函数一一对应的离散梯
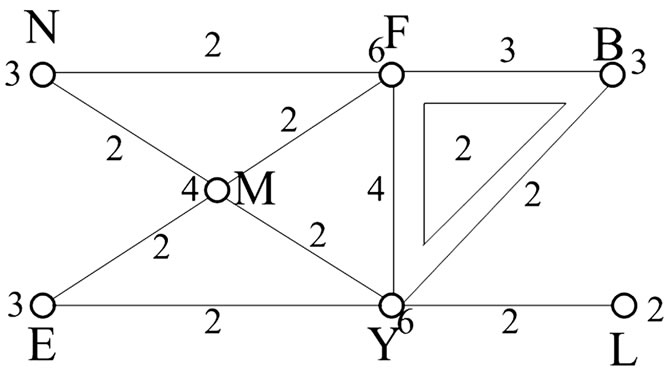
Figure 3. Constructing simplicial complex by the Hasse diagram
图3. 由Hasse图构造的单纯复形
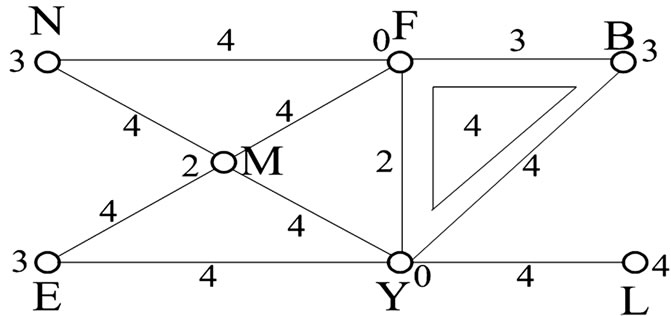
Figure 4. Constructing a discrete Morse function on a simplicial complex
图4. 在单纯复形上构建离散Morse函数
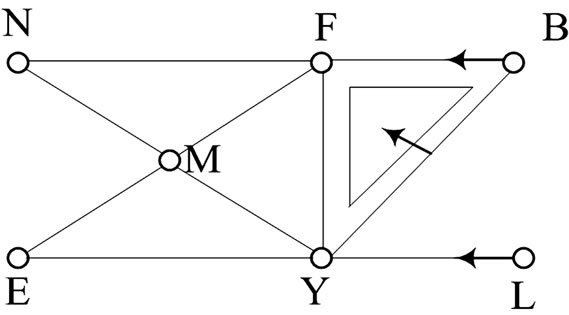
Figure 5. Constructing a Discrete gradient vector field on a simplicial complex
图5. 在单纯复形上构建离散梯度向量域
度向量域。此处用到广义的离散Morse方法的知识,在单元维数较高而离散Morse函数值却不高的单元之间画一个箭头,箭头由低维单元指向高维单元,由此构建了广义的离散梯度向量域(如图5)。
6) 在广义的离散梯度向量域中,箭头表示{合并单元的条件}属于类{购买电脑},由此可得到购买电脑的类成员。在此处{L→Y}表示{L, Y}属于{购买电脑}类,即满足条件{年龄 < 30,学生}属于类{购买电脑}。同理,我们可以得到
{年龄 > 40,信誉一般}属于类{购买电脑};
{年龄 > 40,信誉一般,是学生}属于类{购买电脑}。
总上可得到一个分类规则:
{年龄 < 30,学生}属于类{购买电脑};
{年龄 > 40,信誉一般}属于类{购买电脑};
{年龄 > 40,信誉一般,是学生}属于类{购买电脑};
{年龄 ≤ 30,不是学生}属于类{不购买电脑};
{年龄 > 40,信誉良好}属于类{不购买电脑}。
5. 结束语
分类是数据分析形式之一,可以用于提取描述重要数据类的模型或预测未来的数据趋势,也使我们日常生活更加快捷、简便。本文研究了构建离散Morse函数和离散梯度向量域的方法,并首次把离散Morse方法应用到分类规则挖掘上,使得分类规则更加直观、方便。
6. 致谢
首先我要感谢我的导师刘希玉教授,感谢他在我的学习和研究中对我的帮助和指导!感谢国家科学基金(No.61170038),山东省自然科学基金(No.ZR2011- FM001)对论文的资助和支持!感谢参考文献的作者及其论文给予我的思路和知识资料!感谢我身边的同学和朋友的关心和理解!