滚道剥落对圆柱滚子轴承动态特性影响研究

Influence of Raceway Spalling on the Dynamic Characteristics of Cylindrical Roller Bearings

摘要: 滚道剥落是滚动轴承的一种重要失效形式。本文以N205EM圆柱滚子轴承为对象，建立其有限元动力学分析模型，研究单处及多处滚道剥落对轴承动态特性的影响规律。研究结果表明：滚道剥落的存在会降低轴承的振动稳定性和传动精度；滚道剥落位置的增加，将使轴承产生卡死现象的机率上升；滚道剥落位置越多，轴承的振动稳定性和传动精度越差；在剥落位置达到3处以前，应对轴承进行及时更换。研究结论可以为滚动轴承的选取和设计提供参考。

Abstract: Raceway spalling is an important failure form for rolling bearings. In this paper, the N205EM cy-lindrical roller bearing is used as the object to establish the finite element dynamics analysis model, and the influence of single and multiple raceway spalling on the dynamic characteristics of bearing is studied. The results show that the existence of raceway spalling will reduce the vibration stability and transmission accuracy of bearing; an increase in raceway spalling number will increase the probability of bearing jamming; the more the number of raceway spalling, the worse the vibration stability and transmission accuracy; bearing should be replaced in time before spalling number reaches three. The research conclusion can provide reference for rolling bearing selection and design.

1. 引言

动轴承在各种旋转机械设备中应用广泛，是极为重要的传动零部件，直接影响着旋转机械的运行性能。通常在润滑良好、安装正确、防尘防潮严密条件下正常运转的滚动轴承，其失效形式一般为疲劳失效 [1] [2] 。疲劳剥落是轴承疲劳失效的一种重要形式。近年来，国内外研究学者对疲劳剥落如何影响滚动轴承运行状态开展了大量研究。Petersen等 [3] 对外圈含轴向贯穿剥落滚动轴承的载荷分布进行了研究。尹保健 [4] 研究了沟道点缺陷和椭圆缺陷附近的静力学分布特征。丁为民等 [5] 开展了缺陷形貌对轴承内部载荷分布的影响研究。Rafsanjani等 [6] 提出了一种解析模型，可用于分析含剥落滚动轴承的运动学性能。祝志芳等 [7] 对外圈存在局部缺陷的滚动轴承进行了动力学仿真分析。朱成九等 [8] 建立了含点缺陷滚动轴承的三维模型，分析了含点缺陷滚动轴承的动力学性能。

本文以N205EM型圆柱滚子轴承为对象，开展外圈滚道剥落对轴承动力学性能影响规律的研究，以期为滚动轴承的设计和应用提供理论指导。

2. 显式动力学有限元模型

2.1. 圆柱滚子轴承几何参数

N205EM型圆柱滚子轴承的几何尺寸参数如表1所示。

Table 1. Dimensional parameters of N205EM cylindrical roller bearing

表1. N205EM型圆柱滚子轴承尺寸参数

2.2. 建模过程

滚动轴承各组成部件相互接触部位均为曲面，为保证模型具有较好的曲面轮廓，需对接触表面网格进行加密处理。而在网格划分较密时，显式动力学分析过程通常耗时巨大。为保证模型分析精度，同时减少分析时长，本文将三维滚动轴承简化为二维平面模型，在此基础上，开展滚道剥落对轴承动态特性影响规律的研究。

利用Abaqus有限元软件对N205EM型圆柱滚子轴承进行显式动力学建模，所建立轴承有限元模型网格分布如图1所示。为减少模型计算时间。模型网格采用平面应变单元，单元类型为CPE4R，共12,536个单元，13,664个节点。

根据滚动轴承实际运行状态，对有限元模型的边界条件进行设置，即轴承外圈固定，内圈、滚柱及保持架均不限制其平动和转动自由度。轴承运行工况为内圈受到1000 N径向载荷的作用，同时以1000 r/min的转速绕轴心逆时针转动，如图1所示。

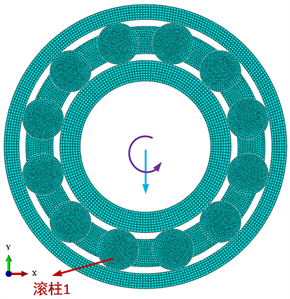
Figure 1. Finite element model and mesh generation of rolling bearing

图1. 滚动轴承有限元模型及网格划分

N205EM型圆柱滚子轴承材料为普通轴承钢，其材料参数为：弹性模量210 GPa、泊松比0.3、密度7800 kg/m³。根据文献 [9] ，将保持架设为刚体，可以有效减少模型计算时间，且不会明显影响模型分析精度。为进一步减少模型计算时间，本文模型对保持架进行了刚体简化处理。滚柱与内、外圈及保持架采用面面接触，摩擦系数设为0.05。

2.3. ABAQUS显式动力学

本文选择Abaqus显式动力学求解器Dynamic/Explicit分析轴承动力学问题，显式动力学求解器Dynamic/Explicit在计算效率、收敛性、不连续性问题等方面明显优于隐式动力学求解器Dynamic/Implicit，更适合本文中轴承动力学模拟这类非线性问题。

动力学分析相较于静力学，多了质量惯性的影响，其系统平衡方程如式(1)所示：

$\mathrm{M}\ddot{a}\left(t\right)+\text{C}\stackrel{\dot{}}{a}\left(t\right)+\text{K}a\left(t\right)=\text{Q}\left(t\right)$ (1)

式中， $\ddot{a}\left(t\right)$ 为加速度， $\stackrel{\dot{}}{a}\left(t\right)$ 为速度；M为质量矩阵；C为阻尼矩阵；K为刚度系数； $\text{Q}\left(t\right)$ 为载荷；t为时间。

在Dynamic/Explicit求解器中，迭代过程是通过中心差分法实现的，其中速度，加速度，位移可通过中心差分分别由(2) (3)式表示：

${\stackrel{\dot{}}{u}}^{\left(i+\frac{1}{2}\right)}={\stackrel{\dot{}}{u}}^{\left(i-\frac{1}{2}\right)}+\frac{\Delta t^{\left(i+1\right)}+\Delta t^{\left(i\right)}}{2}{\ddot{u}}^{\left(i\right)}$ (2)

$u^{\left(i+1\right)}=u^{\left(i\right)}+\Delta t^{\left(i+1\right)}{\stackrel{\dot{}}{u}}^{\left(i+\frac{1}{2}\right)}$ (3)

式中： $\stackrel{\dot{}}{u}$ 为速度； $\ddot{u}$ 为加速度。

3. 结果与讨论

3.1. 单处剥落的影响

本节开展单处剥落对滚动轴承动态特性影响规律的研究。剥落位置如图2所示，位于外圈滚道最底部。剥落形状是深度为1 mm，宽度为3 mm的矩形。

Figure 2. Single raceway spalling

图2. 单处滚道剥落

加速度随时间变化的曲线可以体现出滚动轴承的振动性能。图3为内圈在载荷加载方向的加速度变化曲线。从图中可以看出，存在外圈剥落的轴承，其加速度变化幅度整体要比不存在剥落的轴承大，说明剥落的存在会使轴承的振动性能发生退化，降低轴承的运行稳定性。

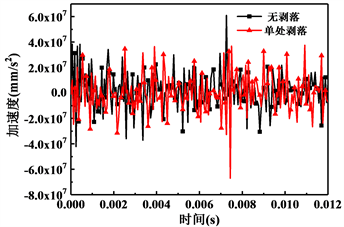
Figure 3. Acceleration curve of inner ring along loading direction

图3. 内圈沿载荷加载方向加速度变化曲线

轴承内圈通常与传动轴通过过盈配合的方式进行连接，即内圈位移的变化直接决定着传动轴的传动精度。内圈沿载荷加载方向的位移变化曲线如图4所示。本模型滚柱通过剥落处的时间大约在0.048 s到0.078 s之间，而从图4可以清晰地看出，当滚子通过剥落位置处时，内圈的径向位移发生了明显的增大。这说明剥落的存在，会降低轴承的传动精度，进而使传动轴的传动精度下降。

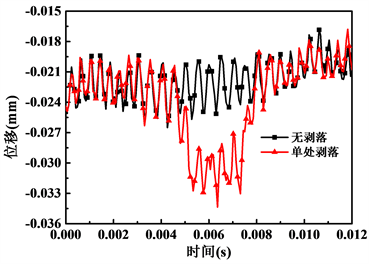
Figure 4. Displacement curve of inner ring along loading direction

图4. 内圈沿加载方向位移变化曲线

滚柱通过剥落位置处时，滚柱与外圈滚道处于何种接触状态，也是我们较为关心的问题。滚柱与滚道间的实际接触状态可以通过分析滚子与外圈滚道的接触受力情况得以反映。图5为滚柱1与外圈滚道的接触力随时间的变化曲线。由图可知，在滚柱通过剥落位置前后，两种情况下滚柱与外圈滚道的接触力大小基本一致。对于存在剥落的情形，当滚子通过剥落处时，滚子与滚道间的接触力瞬间降为零，说明此时滚子与滚道已经脱离了接触状态。

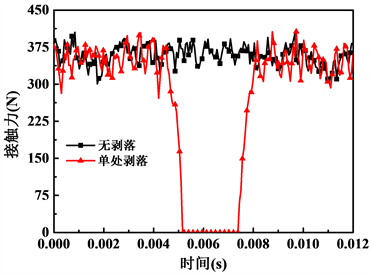
Figure 5. Change curve of contact force between roller 1 and outer ring

图5. 滚柱1与外圈接触力变化曲线

图6为最大应力随时间的变化曲线。从图中可以看出，对于存在外圈剥落的轴承，当滚子通过剥落处时，其最大应力要明显大于正常轴承。而由前面的分析可知，滚柱1通过剥落位置处时，其与外圈处于脱离接触状态。此时，轴承的承载滚柱由6个减少为5个，相应地，每个滚柱所承受载荷增大，导致轴承最大应力变大。轴承处于较大应力状态下工作，会使轴承加速破坏。

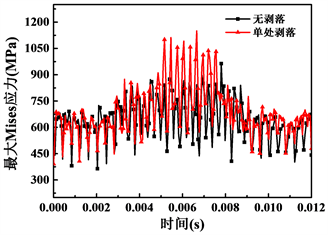
Figure 6. Maximum von Mises stress curve of bearing

图6. 轴承最大von Mises应力变化曲线

3.2. 多处剥落的影响

本节研究多处剥落对滚动轴承动态特性的影响规律。剥落位置如图7所示，剥落位置分别为3处和5处。

(a) 3处 (b) 5处

Figure 7. Several raceways peeling off

图7. 多处滚道剥落

图8给出了轴承内圈沿载荷加载方向的加速度变化曲线。由图可知，随着剥落位置的增多，轴承加速度的变化幅度整体上呈现逐渐增大的现象，说明剥落数量越多，轴承的振动稳定性越差。另一方面，我们可以看出，当剥落位置为5处时，内圈加速度变化幅度要小于其他几种情况，这种现象显然是不正常的。造成这种现象的原因，主要是因为在剥落位置为5处时，轴承已不能正常运转，滚柱与外圈滚道发生了卡死，如图9所示。从图9可以看出，在t = 0.05 s和t = 0.10 s时，轴承各组成部件的相对位置几乎未发生变化，负责承载的5个滚柱全部陷入剥落中，说明轴承发生卡死。

图10为轴承内圈沿载荷加载方向的位移曲线图。由图可知，随着剥落发生位置的增多，内圈位移峰值逐渐增大，说明剥落数量越多，轴承传动精度越低。剥落发生位置为单处时，内圈位移大小与不存在剥落的轴承相对不大，运行精度在一定程度上仍可接受。而当剥落位置增至3处及以上后，位移大小变化幅度大幅增加，此时轴承已不能满足其正常工作时的传动精度。而当剥落发生位置为5处时，轴承发生卡死，内圈位移从0.025 mm瞬间增加至0.30 mm左右，此后一直保持不变。综上分析可知，在剥落发生位置等于或多于3处时，轴承已不能正常工作。因此，应在剥落发生位置达到3处以前，及时对轴承予以更换。

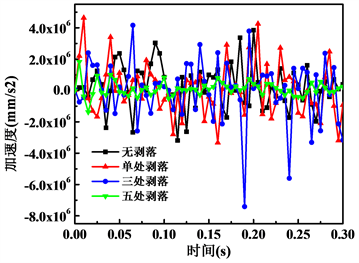
Figure 8. Acceleration curve of inner ring along loading direction

图8. 内圈沿载荷加载方向加速度变化曲线

(a) t = 0.05 s (b) t = 0.10 s

Figure 9. Running state of rolling bearing

图9. 滚动轴承运行状态

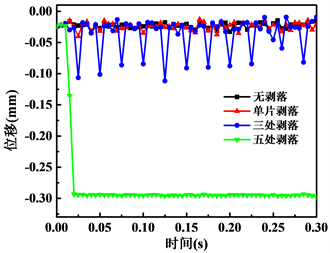
Figure 10. Running state of rolling bearing

图10. 内圈沿载荷加载方向位移变化曲线

4. 结论

在Abaqus有限元软件中建立了存在外圈滚道剥落的圆柱滚子轴承显式动力学有限元分析模型。通过分析研究，得到如下结论：

1) 疲劳剥落的存在会降低滚动轴承的振动性能和传动精度，并加速轴承破坏。

2) 存在单处疲劳剥落的滚动轴承，其动态运行性能要优于多处疲劳剥落的滚动轴承。

3) 剥落发生位置不小于3处时，滚动轴承即不能正常工作。在剥落发生位置达到3处以前，应及时对轴承进行更换。

基金项目

国家重点研发计划(2017YFB1300600)；中国博士后科学基金(2017M623026)。