1. 引言
在本文中,arthr表示反双曲正切函数。对
,记 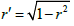 。对于正实数x和y,Γ-函数、B-函数以及ψ-函数分别定义 [1] 为:
。对于正实数x和y,Γ-函数、B-函数以及ψ-函数分别定义 [1] 为:
(1)
令
,是Euler-Mascheroni常数,则
,
(2)
在
上定义Ramanujan常数 [2] [3] 为:
(3)
当
时,式(3)记为
,
结合式(2)~(3)知
。
给定实数a,b,
,高斯超几何函数定义 [4] 为:
,
(4)
这里,当
时,
,且
。
当
,第一类、第二类广义椭圆积分分别定义 [5] 为:
(5)
(6)
因广义椭圆积分关于参数a的对称性,本文只考虑
的情形。特别地,当
时,
与
分别为第一类和第二类完全椭圆积分。
广义Grötzsch环函数
定义 [6] 为:
(7)
显然,当
时,
表示平面拟共形映射单调递减的Grötzsch极值环
的模,这里的
表示平面单位圆盘,且
,
。近几年,国内外很多学者对广义Grötzsch环函数的单调性、凹凸性及不等式进行研究,见文献 [7] [8] [9] 。
符号差
的p次广义Ramanujan模方程定义 [5] 为:
(8)
利用式(5)及式(7),可将式(8)改写成
(9)
式(9)的解可以表示为
,
(10)
称式(10)中的函数
为广义Hersch-Pfluger偏差函数,
,
。当
时,
退化为Hersch-Pfluger偏差函数
。此外,许多学者对广义Hersch-Pfluger偏差函数的性质做了深入的研究,见文献 [10] [11] 。
在文 [6] 中,裘松良获得如下结论:当
,
时,不等式成立
当
时等号成立,其中
。
在文 [7] 中,王根娣等揭示了广义Hersch-Pfluger偏差函数与广义Grötzsch环函数
的关系:
(11)
当且仅当
。
本文主要揭示广义Grötzsch环函数的分析性质,获得新的精确不等式,并应用于Ramanujan模方程解的精确估计。
2. 引理
本文为了证明第三部分的主要结果和引用方便,需要引入下面的导数公式 [4] :
,
(12)
(13)
引理1 ( [4] , Theorem 1.25)对
,设f和g是两个实值函数,并都在
上连续,在 (a,b)上可微且在
上
,如果
在
上单调递增(递减),那么函数
和
也在
上单调递增(递减)。而且,若
的单调性是严格的,则F和G的单调性也是严格的。
引理2 ( [5] , Lemma 5.4)对任意的
及
,则
(1)
从
到
上严格单调递增。
(2)
从
到
上严格单调递减。
引理3 ( [11] ,定理2.1(3))对任意的
及
,则
从
到
上严格单调递增。
3. 主要结果及证明
利用上述引理,本节给出主要结果及证明。
定理3.1 设
,则函数
从
到
上严格单调递增。特别地,当
时,
(14)
证明:令
,
,则
,
。由式(12)、(13),求导得
根据引理2.2 (1)、(2)及引理2.3可知,
是三个正的单调递增函数的乘积。由引理2.1可得函数
的单调性。显然,
。根据l’Hôpital法则,结合引理2.1~2.3,极限
.
显然,不等式(14)成立。
定理3.2设
,
,
,则函数
从
到
上严格单调递增。特别地,当
时,
(15)
证明:令
, 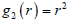 ,则
,则  ,
。结合式(13),求导得
,
。结合式(13),求导得
由文 [7] 中定理1 (1)和引理2.1 (3)、引理2 (2)可知,
是四个正的且单调递增的函数乘积。结合引理2.1可知
的单调性。极限值
。结合文 [7] 中引理2.1 (3)、引理2 (2),运用l’Hôpital法则便知
.
推论3.3对所有的
和
时,成立不等式
(16)
特别地当
时,不等式退化为
(17)
证明:根据式(11)及定理3.2的结论易得不等式(16)和(17)。
基金项目
浙江省教育厅科研基金项目(Y201635387),浙江机电职业技术学院科研项目(A027117021),浙江省高等学校访问学者项目(FX2018093)。
参考文献
NOTES
*通讯作者。