1. 引言与预备知识
定义1.1 [1] 我们把正整数集记为
,
称为自然数集。
定义1.2 [2] 设X是一个集合,记刻划X中所含元素数量的概念为基数,记为
.如果X是空集或者存在正整数
,使得集合
和集合
之间有一个一一映射,则称集合X是一个有限集。
定义1.3 [3] 在度量空间
中,定义公式
为x的一个
-邻域。
定义1.4 [4] 设
是两个度量空间,
。若对于
的任何一个球形邻域
,存在
某一个球形邻域
,使得
,则称f在点
处连续。若f在X的每一点处都连续,则称f是一个连续映射。
定义1.5 [5] 设
为动力系统,
,称集合
为x在f之下的轨道,记为
或
。
定义1.6 [6] 设
为动力系统。对
,如果对任意
,存在自然数m和有限点列
,使得
且
,则称此点列是从
到
的一个
链,则称点
为f的一个链回归点,f所有的链回归点构成的集合称为链回归点集,记为
。
定义1.7 [7] 设
是集合X到自身的一个映射,记“
”其中id表示恒同映射,我们称
为f的n次迭代。
定义1.8 [8] 我们把类帐篷映射定义为:
当
时,
,当
时,
。记
为
的不动点,记
为
在
上的斜率,
为
在
上的斜率。
。本节主要讨论
时的情形,当
时,记
,
,则
,且
。
2. 相关引理
引理2.1:对任意的
,及
,若
,则
。
证明:因为
,所以
,
,而
,所以
(*)。另一方面,因为
,令
。所以
且
。因为
在同一条直线上
,所以,我们可得
,由
得
从而
。同样由
得
(**)。所以由(*),(**)得,
。
引理2.2:对任意的
,及
,存在
,使
。
证明:若
,则由引理2.1知
,若对某一个
,当
时,
,当
时,
且
使得
且
。所以
因为
,所以若不存在n,使得
,则
,这与
矛盾。所以存在
,使得
且当 时,
时, 。记
。记 。所以
。所以 。因为
。因为 ,所以存在
,所以存在 ,且
,且 ,使得
,使得 。
。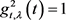 ,
, (1)。由于
(1)。由于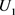 是
是 的
的 邻域,所以存在
邻域,所以存在 。使得
。使得 ,即
,即 ,所以
,所以 。
。
因为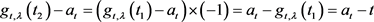 。所以
。所以
 。因为
。因为 ,所以存在
,所以存在 ,使得
,使得 ,所以
,所以 ,
, (2),由(1),(2)知
(2),由(1),(2)知 所以
所以 ,证明完毕。
,证明完毕。
命题2.1:对任意的 ,及
,及 ,存在从
,存在从 到x的关于
到x的关于 的
的 链。
链。
证明:设 ,由引理2.2,存在n,使得
,由引理2.2,存在n,使得 所以存在
所以存在 ,使得
,使得 ,记
,记 。则
。则 是一条从
是一条从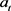 到x的关于
到x的关于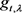 的
的 链。
链。
引理2.3:对任意区间U,若 ,则
,则 ,其中
,其中 。
。
证明:不妨设 ,则
,则 ,
, ,所以
,所以 ,又
,又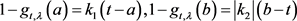 。若
。若 。则
。则 ,因而
,因而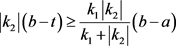 。若
。若 ,则
,则 ,同样有
,同样有 ,由此可得
,由此可得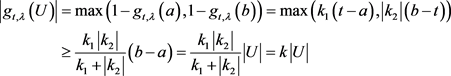 。
。
命题2.2:设 ,若U为一个区间满足
,若U为一个区间满足 且当
且当 时,
时, 。则
。则 ,其中
,其中 。
。
证明:不妨设 ,则
,则 且
且
情形1: 。此时由引理2.3
。此时由引理2.3 ,此时
,此时 ,其中
,其中 。所以
。所以
 ,所以
,所以 。
。
显然上式关于 单调增加,
单调增加, 。
。
所以 。
。
因为 ,所以
,所以 ,另一方面,当
,另一方面,当 时,
时, 关于t单调增加,所以
关于t单调增加,所以
 ,因为
,因为 ,所以
,所以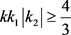 ,即有
,即有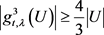 。
。
情形2,若 ,则
,则 ,进一步
,进一步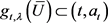 ,则
,则 且
且 ,若
,若 ,则
,则 ,且
,且 ,因为
,因为 ,所以
,所以 ,所以
,所以 。
。
情形3,若 。则
。则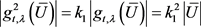 。
。
进一步,若 ,则
,则 。
。
若 ,则
,则 。
。
若 ,则由引理2.3,
,则由引理2.3,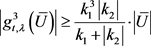 。
。
此时存在 ,使得
,使得 ,即有
,即有
 ,所以
,所以 ,因为
,因为 ,即
,即 ,所以
,所以 或
或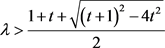 。
。
因为此时 ,所以
,所以 (舍去)。
(舍去)。
所以 。
。
考虑当 时,
时, 。
。
当 时,
时, ,所以
,所以 。从而
。从而 。
。
又当 时,
时, ,当
,当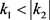 时,
时,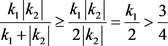 。
。
因为 ,所以
,所以 。
。
取 ,则
,则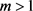 ,且由情形1~3知
,且由情形1~3知 。
。
命题2.3:设 ,若U为一个区间满足
,若U为一个区间满足 ,且
,且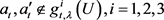 则
则 。
。
证明:因为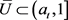 ,所以
,所以 且
且 ,从而
,从而
 .
.
情形1 ,则
,则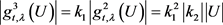 ,因为
,因为

所以 。
。
情形2 ,则
,则 。
。
因为 ,所以
,所以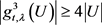 。
。
情形3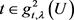 ,此时由引理2.3知,
,此时由引理2.3知,
由情形1~3知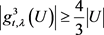 。
。
命题2.4:设 ,U为一个区间满足:
,U为一个区间满足: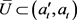 且
且 。
。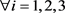 ,
, ,则
,则 。
。
证明:由引理2.3, 且存在
且存在 ,使得
,使得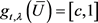 ,所以
,所以 且
且 ,所以
,所以
 .
.
命题2.5:设 ,U为一个区间满足:
,U为一个区间满足: 且
且 ,
, ,则
,则 。
。
证明:在命题条件下,我们有 且
且 ,因为
,因为 且
且 ,所以
,所以 。由命题2.3的证明过程知
。由命题2.3的证明过程知 。
。
命题2.6:设 。则存在
。则存在 。使得
。使得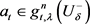 。
。
证明:若结论不成立。则对于任意的 。
。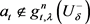 ,
, 。对每一个
。对每一个 ,
, 有下列五种情况:
有下列五种情况:
① ;②
;② ;③
;③ ;④
;④ ; ⑤
; ⑤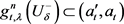 且
且 ;
;
针对情形①②,我们由命题2.2得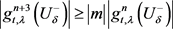
针对情形③,我们由命题2.5得
针对情形④,我们由命题2.3得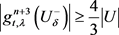
针对情形⑤,我们由命题2.4得
因此,任意的n, ,
, 且
且 。所以
。所以 ,这与
,这与 矛盾.所以结论成立,即存在
矛盾.所以结论成立,即存在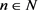 ,使得
,使得 。
。
命题2.7:对对任意的非退化闭区间U,当 时,存在无穷多个
时,存在无穷多个 使得
使得 。
。
证明:若结论不成立,则存在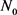 ,对任意的
,对任意的 我们有
我们有 或
或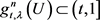 若
若 则
则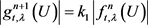 ,若
,若 则
则 ,令
,令 于是对于任意的
于是对于任意的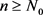 ,我们有
,我们有 ,从而
,从而 ,矛盾。
,矛盾。
命题2.8:设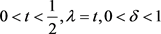 。则存在
。则存在 。使得
。使得 。
。
证明:若结论不成立,则对任意的 ,
, ,
,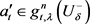 ,有前面引理知,存在
,有前面引理知,存在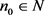 ,使得
,使得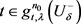 ,所以
,所以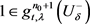 ,
,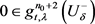 ,
, ,
, ,
,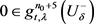 ,
, ,归纳得
,归纳得 ,
, ,
,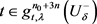 ,
, 因为任意的
因为任意的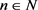 ,
,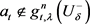 ,
, ,所以
,所以 ,
,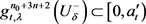 ,
,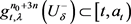 。所以任意的
。所以任意的 ,
,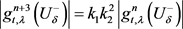 因为
因为 ,所以
,所以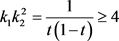 ,所以
,所以 所以
所以 ,矛盾。所以结论成立。
,矛盾。所以结论成立。
命题2.9:设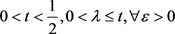 ,
, ,存在从x到
,存在从x到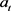 的关于
的关于 的
的 链。
链。
证明:由 的连续性知,对任意的
的连续性知,对任意的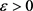 ,存在
,存在 ,当
,当 时,
时, 。由引理命题2.6和命题2.7知:任意满足
。由引理命题2.6和命题2.7知:任意满足 的正数
的正数 ,存在
,存在 ,使得
,使得 。所以,对任意的
。所以,对任意的 ,总存在
,总存在 使得
使得 则对于链
则对于链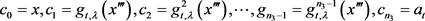 ,有
,有 ,则
,则 是一条从x到
是一条从x到 的
的 链。命题得证。
链。命题得证。
3. 主要定理的证明
定理3.1: ,
, 。
。
证明:当 时,任意的
时,任意的 ,由命题2.9知,存在从x到
,由命题2.9知,存在从x到 的关于
的关于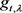 的
的 链,又由命题2.1知对任意的
链,又由命题2.1知对任意的 ,及
,及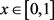 ,存在从
,存在从 到x的关于
到x的关于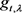 的
的 链,所以
链,所以 。
。