1. 引言
开关磁阻电机(以下简称SRM)因简单的双凸极定转子结构,且不含永磁体,所以具备在恶劣环境条件下运转稳定、制造成本低廉、效率高及抗高温等一系列优点。近年来,SRM电机使用范围越来越广 [1] [2] [3] 。但由于SRM固有的双凸极结构和特有驱动方式,它的径向磁吸力和转矩脉动比传统交、直流电机都要高,过大径向磁吸力会带来电机振动和噪音问题,已成为制约SRM使用和发展的一个重要问题 [4] [5] 。
由于SRM电机定子绕组中通有励磁电流作用,在定、转子齿间存在磁场力,可沿切向和径向两方向进行分解。其径向分力对电机运行无作用,但会使定子受到应力造成形变导致振动和噪音。当径向力谐波和定子固有频率接近或相等时,将产生激烈振动和噪音 [6] [7] 。所以可知控制定子振动关键点就是如何有效减小径向力。本文为降低径向力,抑制电机振动,对转子齿结构进行了优化设计,即以转子齿中心线为轴,对称开槽,利用有限元软件Ansoft Maxwell建立2D模型,并分析了槽尺寸对电机径向力的影响 [8] 。
2. SRM振动分析
在运行的SRM定、转子磁极间存在磁场力。这种磁场力可沿径向和切向进行分解。径向力与电磁转矩大小无关,但会使定子形变导致振动和噪音,更严重的情况是径向力谐波与定子固有频率相近或相等时,严重的共振现象就会产生。所以,分析并减小径向力是降低振动、减噪的关键 [9] [10] 。
线性假设下径向磁吸力为:
(1)
单相电磁转矩为:
(2)
由式(2)知:随着励磁电流的增大径向磁吸力也会增大。在相同励磁电流时,随着电机定转子位置改变,产生的径向力较大且定转子中线完全对齐时达到顶峰。
当给SRM一相绕组通电时,径向磁吸力会被产生;停止通电时,该力变为零。当电机运转时,励磁绕组会连续换相,如此径向磁吸力会重复吸引和释放定子轭部,会产生振动,甚至更严重的共振。若径向力能有效得到抑制,则就会达到减振、降噪效果。径向力的求解通常使用有限元法和磁导法,本文主要使用有限元法 [11] 。
3. SRM的结构
目前主要对SRM的定、转子尺寸和结构、气隙长度等方面来优化电机本体结构,实现改变电机运行性能。本文主要对转子齿结构进行优化设计,改变转子齿部磁场分布和调整气隙磁场,降低磁径向力从而抑制振动。文献 [12] 中提到为抑制SRM振动噪音,一些专家学者做了很多工作,SRM定/转子结构的改进是方法之一。可以在定/转子齿部开设一定形状、尺寸的槽,改变磁力线的位置,实现降低定转子重叠部分的有效径向力,并提到降低径向力效果主要取决于开槽宽度而非厚度。本文以三相12/8极SRM为例 [13] ,对常规电机转子齿部做了一定改进,在转子齿部恰当位置开设了槽。常规和改进电机参数如表1所示,其中改进结构中槽的位置和槽宽数据都是以有限元优化仿真结果来确定的。依据电机结构参数,通过绘图软件绘制电机冲片,再导入Ansoft Maxwell有限元软件中建立2D模型。图1(a)、图1(b)分别为原始、改进SRM结构。

Table 1. Main parameters of the motors
表1. 电机主要参数
 (a) (b)
(a) (b)
Figure 1. Contrast structure diagram of SRM
图1. SRM对比结构图
4. 有限元仿真分析
4.1. 磁路分析
本文所研究的SRM电机,额定转速为3000 r/min,额定电压为140 V,进行磁路分析。磁路分析如图2所示。
 (a) (b)
(a) (b)
Figure 2. Contrast diagram of air-gap magnetic field; (a) Conventional air-gap magnetic field; (b) Rotor slotted air-gap magnetic field
图2. 气隙磁场对比图;(a) 常规气隙磁场;(b) 转子开槽气隙磁场
图2(a)为常规结构下定转子未对齐时,定转子重叠区域的气隙磁力线分布图,图2(b)为转子齿部分开槽结构下,定转子对齐情况与常规一样情况下磁力线分布,两种情况下定转子重叠位置角和励磁电流都一样。可以得出:由于在转子齿部开了槽,使转子齿顶部分磁力线发生较大偏转,有的甚至有法线方向完全偏转成切向方向。因此降低了气隙径向磁密,使切向磁密增强。
4.2. 转子槽位置和宽度优化
从图2(b)可知,转子齿部槽的位置和尺寸对气隙磁力线分布造成重大影响,槽的宽度要恰当选择,否则会引起转子齿部磁路饱和,且根据文献 [12] 论述转子极中心开槽降低径向力的效果主要取决于槽的宽度而不是厚度。所以对转子开槽的位置和宽度进行了优化设计,并最终确定了槽的位置和槽宽数据。
优化设计时,选用静态磁场情况来进行。优化情况如图3、图4所示。
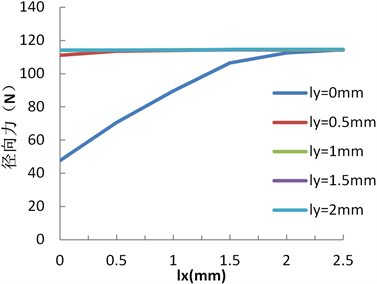
Figure 3. Radial force optimization diagram
图3. 径向力优化图
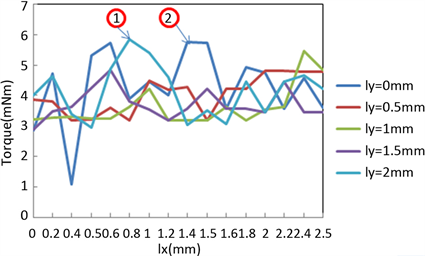
Figure 4. Electromagnetic torque optimization diagram
图4. 电磁力矩优化图
以如图1(b)中A2下矩形槽右上端点为基准点,来代表槽位置进行优化,该基准点在软件中的坐标为(5 mm, 34 mm)。图3,图4中lx,ly分别表示该基准点横、纵坐标的减少值。从图3可得:ly = 0 mm径向力最小;从图4可得:1和2点对应电磁力矩最大,但1点对应ly = 2 mm径向力偏大,所以综合比较点2是最佳点,于是lx优化值也就确定了。优化结果为ly = 0 mm,lx = 1.4 mm,槽宽为7.2 mm,且上述基准点坐标也就确定,槽的最佳位置随之确定,对应基准点的坐标为(3.6 mm,34 mm)。
4.3. 瞬态分析
利用Maxwell Circuit Editor设计了SRM的驱动电路,并对激励方式进行了对应设置,实现了有限元的瞬态分析。径向、切向磁密对比如图5、图6所示。
由图5可知:改进的结构降低了径向磁密大小,原结构中径向磁密最大值为0.7 T,通过开槽优化后,降至0.6 T。由图6可知,切向磁密经过开槽优化后,得到了提升。原结构中最大值为0.25 T,提升到0.34 T,提升了36%。如此降低有效径向力,且增大了切向磁密,实现电磁转矩提升。
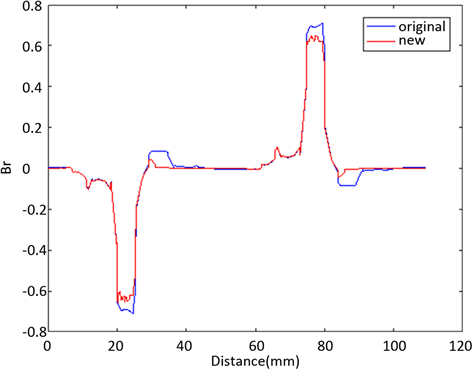
Figure 5. Radial magnetic density contrast diagram
图5. 径向磁密对比图
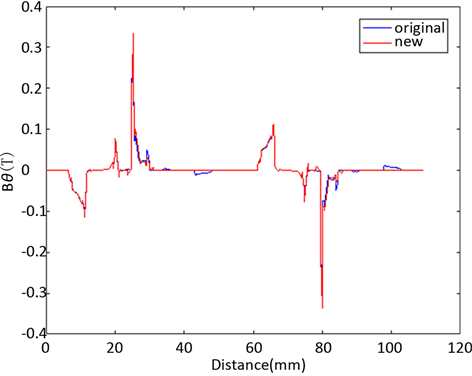
Figure 6. Tangential magnetic density contrast diagram
图6. 切向磁密对比图
5. 结论
本文通过在SRM电机转子齿部分合适位置开了槽,对电机内部磁力线分布进行了调整,改善了气隙磁场。通过建立2D仿真模型,并对转子齿开槽位置及槽宽度数值做了有限元优化计算,最终确定最优值。依据仿真结果可知优选槽位置和槽宽度数值后,在提升气隙切向磁密的基础上,有效降低径向磁密,最终实现降低振动、噪音的目的。