基于Swish激活函数的人脸情绪识别的深度学习模型研究

A Research on Deep Learning Model for Face Emotion Recognition Based on Swish Activation Function

摘要: 近年来，深度学习模型得到飞速发展，深度卷积神经网络作为其中一种方法在计算机视觉中得到广泛应用。影响深度学习模型性能的因素众多，其中激活函数的选取和神经网络的结构对深度学习模型的性能有着重要的影响。本文分析了传统激活函数与新型Swish激活函数的优缺点，将Swish函数引入人脸情绪深度学习模型，提出了一种改进的反向传播算法，并在卷积神经网络中使用多层小尺寸卷积模块替代大尺寸卷积模块，提取细化特征，构建了一种新型的人脸情绪识别深度学习模型Swish-FER-CNNs。实验结果表明，相比于ReLU、L-ReLU、P-ReLU等激活函数，基于Swish激活函数的深度学习模型的识别准确率更高。结合改进的网络结构，本文构建的深度学习模型Swish-FER-CNNS相对于现存模型，识别准确率提高了4.02%。

Abstract: In recent years, deep learning model has been developed rapidly. As one of the methods, deep convolution neural network has been widely used in computer vision. There are many factors af-fecting the performance of deep learning model, among which the selection of activation function and the structure of neural network have important impact on the performance of deep learning model. This paper analyses the advantages and disadvantages of the traditional activation function and the new Swish activation function, introduces Swish function into the deep learning model of facial emotion, proposes an improved back propagation algorithm, and uses multi-layer small-size convolution module instead of large-size convolution module in the convolution neural network to extract refinement features, and constructs a new deep learning model of facial emotion recognition, Swish-FER-CNNs. The experimental results show that the recognition accuracy of deep learning model based on Swish activation function is higher than that of activation functions such as ReLU, L-ReLU and P-ReLU. With the improved network structure, the recognition accuracy of the deep learning model of Swish-FER-CNNS constructed in the paper is improved by 4.02% compared with the existing model.

1. 引言

本人类通过眼睛感知光信息洞悉世界，情绪是人类沟通的一个重要组成部分，影响人类的交流。准确分析人脸情绪，对深入理解人类行为至关重要。在文献 [1] [2] 中，Giannopoulos等人已经提出了使用卷积神经网络的方法分析人脸情绪。

卷积神经网络系统主要由卷积层、池化层、激活函数、全连接层、分类函数等多部分组成 [3] [4] ，组成的方式不同导致网络模型的性能差异显著。经典的AlexNet深度学习模型使用5层卷积层、3层全连接层、ReLU激活函数等联接构成的网络，在ImageNet分类上准确率提高显著 [5] [6] [7] [8] [9] ，但参数较多、计算负载大，在人脸情绪识别数据集上有过拟合的问题。Jeon [10] 在AlexNet的基础上进行了结构精简，成功地将其引入人脸情绪识别领域，但网络层数较浅，模型拟性能较弱，识别准确率不高。

卷积神经网络自学习机制的关键是反向传播算法，系统产生的误差通过网络结构向后传播，调节系统自身参数 [11] 。激活函数 [12] [13] [14] 作为反向传播算法中重要的组成部分，表示神经元潜在动作的抽象映射，影响系统性能。ReLU激活函数 [5] 是线性整流函数(Rectified Linear Unit)，又称修正线性单元。加强了模型的非线性并且可以提高模型的收敛速度。但当x < 0时，ReLU的输出皆为0，导致模型无法迭代，出现神经元死亡和均值偏移问题。之后，Maas提出的L-ReLU激活函数，即带泄露整流函数(Leaky ReLU)，能在一定程度上解决了这些问题，但在x < 0时为线性函数，系统鲁棒性较差 [15] [16] [17] 。文献 [18] [19] 中提出的P-ReLU被称为参数线性整流函数(Parametric ReLU)，与L-ReLU相似，不同之处在于当x < 0时，斜率为系统学习所得，函数性能提高，但仍未解决对输入噪声鲁棒性较差的问题。

为更好地拟合数据与系统模型，本文结合Swish激活函数，改进反向传播算法，解决了鲁棒性较差的问题，同时改善了神经元死亡和均值偏移问题。针对AlexNet和Jeon的深度模型(简称Jeon’s)网络层数较浅、参数较多等不足，加深了神经网络层数并使用更小的卷积核，便于感知细化特征，提出了Swish-FER-CNNs情绪识别模型，提高了识别准确率。

2. 基于卷积神经网络的情绪识别模型

卷积神经网络使用卷积层提取图像特征，以池化层简化参数，提高计算效率。采用多层卷积和池化级联能进一步感知和提取图像特征，获取高维特征并使用全连接层将学习到的隐式特征映射到样本标记空间，最后通过Softmax分类器进行分类，得到分类标签，具体模型如图1所示。

Figure 1. Principle diagram of emotion recognition model

图1. 情绪识别模型原理图

2.1. 反向传播算法

传统反向传播算法是调整网络模型的参数更迭的依据。已知输入x通过前馈传播得到 $\hat{y}$ ，产生的误差为代价函数 $J_{\theta }$ 。来自代价函数 $J_{\theta }$ 的信息通过模型向底层传播，用于计算梯度。反向传播算法是一种计算微积分中链式法则的算法，f和t分别是两个实数集合间的映射函数，令f为激活函数， $y=t\left(x\right),z=f\left(t\left(x\right)\right)=f\left(y\right)$ ，则链式法则为：

$\frac{\text{d}z}{\text{d}x}=\frac{\text{d}z}{\text{d}y}\frac{\text{d}y}{\text{d}x}$ (1)

上式可反映上层网络输出z，受下层网络输出x的影响而变化的数学关系。又有 $\frac{\text{d}z}{\text{d}y}=f^{\prime }$ ，故f的选取对于深度学习网络的迭代性能有较大影响。下文通过对Swish激活函数进行性能分析，提出了一种改进的反向传播算法。

2.1.1. 激活函数分析

传统的Sigmoid激活函数，其函数定义如下：

$f\left(x\right)=\frac{1}{1+{\text{e}}^{-x}}$ (2)

其函数曲线如下图2所示：

Figure 2. Sigmoid activation function

图2. Sigmoid激活函数

从图中可知，Sigmoid函数具有软饱和性：函数在定义域范围内，连续可导，在输入极大极小时，函数斜率趋近0，导数趋向于0，被称为梯度弥散。梯度弥散会造成梯度幅度随传播深度增加而急剧减小的现象，神经元权重更新放缓，网络难以训练，不利于神经网络的发展。

为解决激活函数梯度弥散问题，Krizhevsky等人采用ReLU作为激活函数，其定义如下：

$f\left(x\right)=\max \left(0,x\right)$ (3)

ReLU激活函数在 $x>0$ 的定义域内导数恒为定值，反向传播时可简化计算，加快收敛速度。在 $x<0$ 定义域内具有硬饱和特性：输入落在此区域，对应的输出皆为0，神经元反向传播一阶梯度亦为0，神经元不具有激活作用，即神经元死亡，导致模型的拟合力下降。此外，ReLU函数在 $x<0$ 定义域对应输出为0这一特性导致神经元输出均值大于0，不利于迭代计算，此问题被称为均值偏移：后一个神经元的输入为前一个神经元的输出，因输出皆为正值，后一个神经元的输入被限制，模型的拟合能力下降，制约深度模型的性能。

Maas等人引入L-ReLU激活函数可有效解决均值偏移问题，其函数定义为：

$f\left(x\right)=\{\begin{array}{l}x,x\ge 0\\ \alpha x,x<0\end{array}$ (4)

L-ReLU激活函数在 $x\ge 0$ 定义域，一阶导数恒定，利于计算，与ReLU性质一致。在 $x<0$ 定义域内，L-ReLU图像位于y轴的负半轴，减缓了均值偏移。

He Kaiming等人引入P-ReLU激活函数，以获取更贴合模型的负轴斜率，其函数定义为：

$f\left(x\right)=\{\begin{array}{l}x,x\ge 0\\ {\alpha }_{i}x,x<0\end{array}$ (5)

其函数性质与L-ReLU相似，不同之处在于：在 $x<0$ 定义域，斜率 ${\alpha }_i$ 需要模型根据输入数据学习而来，增加了计算复杂度，给系统计算增添了负载。

本文中使用的Swish激活函数的定义如下：

$f\left(x\right)=\alpha *x*sigmoid\left(x\right)$ (6)

其中， $\alpha$ 为常数，本文中将 $\alpha$ 设置为1。函数图像如图3所示。

Figure 3. Swish activation function

图3. Swish激活函数

当 $x>0$ 时，Swish激活函数的一阶导数易于计算，利于模型训练。当 $x<0$ 时，与ReLU函数相比，Swish函数既能够均衡正负轴比重，减缓了均值偏移现象，又由于它无硬饱和性，避免了神经元死亡现象；与L-ReLU函数相比，Swish函数是非线性的，具有软饱和性，鲁棒性更好；与P-ReLU相比，Swish函数不需要计算参数 $\alpha$ ，减少了计算量，且鲁棒性更好。因此，Swish激活函数的性能优于ReLU、L-ReLU和P-ReLU函数。

2.1.2. Swish-FER-CNNs中的反向传播算法

反向传播算法可广泛应用于深度学习梯；度计算，其中包含前馈传播和后馈传播两部分。激活函数是算法的重要组成部分。使用Swish激活函数的前馈传播模型可表示为：

$u^{\left(i\right)}=\text{Swish}\left({{\rm A}}^{\left(i\right)}\right)$ (7)

其中 $u^{\left(i\right)}$ 表示i节点， ${{\rm A}}^{\left(i\right)}$ 是 $u^{\left(i\right)}$ 所有父节点的集合， $\text{Swish}\left(\right)$ 表示激活函数映射操作。

反向传播算法中为计算单个节点损失函数 $u^{\left(n\right)}$ 对 $n_i$ 个输入节点 $u^{\left(1\right)}$ 到 $u^{\left(n_i\right)}$ 的梯度，使用图 $\xi$ 储存前向传播的计算过程及节点数值。定义子图 $\beta$ 在上增添额外节点一组且依赖于 $\xi$ ，以实现后向传播过程及

节点数值存储。 $\beta$ 的计算与 $\xi$ 恰好相反， $\beta$ 中的每个节点导数 $\frac{\delta u^{\left(n\right)}}{\delta u^{\left(i\right)}}$ 与 $\xi$ 中 $u^{\left(i\right)}$ 相关联，可表示为：

$\frac{\partial u^{\left(n\right)}}{\partial u^{\left(i\right)}}={\displaystyle \underset{i,j\in Pa\left(u^{\left(i\right)}\right)}{\sum }\frac{\partial u^{\left(n\right)}}{\partial u^{\left(i\right)}}}\frac{\partial u^{\left(i\right)}}{\partial u^{\left(j\right)}}$ (8)

执行内积，其内积因子一为对于子节点 $u^{\left(i\right)}$ 已计算的梯度 $\frac{\partial u^{\left(n\right)}}{\partial u^{\left(i\right)}}$ ，其因子二为对于子节点 $u^{\left(i\right)}$ 的偏导数 $\frac{\partial u^{\left(i\right)}}{\partial u^{\left(j\right)}}$ 。总而言之， $\xi$ 中每一条边中的计算过程都包含激活函数运算，Swish激活函数的非线性对鲁棒性较强，计算复杂度较低，学习拟合力强，从而提高反向传播算法性能。

改进的反向传播算法使用 $h^{\left(i\right)}$ 表示第i层隐含层输出值， $a^{\left(i\right)}$ 表示激活函数的输入值， $\theta$ 包含所有参数(权值和偏置)， $\Omega \left(\theta \right)$ 为正则式，J为总代价函数，g表示当前位置梯度， $\nabla$ 表示梯度的更迭矢量， $\odot$ 表示矩阵点积。算法对于每一层k都生成了对激活函数输入值 $a^k$ 的梯度，从输出层向后计算梯度一直到第一个隐含层，生成的梯度可视为指导每层输出该如何调整以减小模型误差的依据，再根据以上产生的梯度可以计算得到对每层参数的梯度，从而实现代价函数后馈传播，详细算法如下所示。

2.2. Swish-FER-CNNs网络模型

为适应Kaggle数据48 × 48灰度图像，并进一步提高模型性能，本文优化了网络结构，与改进的反向传播算法相结合，构建了Swish-FER-CNNs深度学习模型。从48 × 48的图像中随机截取42 × 42的灰度图像作为网络的输入。第一层卷积层采用16个大小为3 × 3的卷积核对大小为42 × 42 × 1的输入图像进行卷积操作，输出大小为42 × 42 × 16的特征图，第二层卷积采用32个大小为3×3的卷积核对上一层输出的特征图进行卷积操作，并输出大小为42 × 42 × 32的特征图，池化操作后可获得大小为21 × 21 × 32的特征图，并作为第三层卷积的输入。之后的卷积操作类似于前两层卷积层，第三层和第五层的卷积层输出需用于后续的池化层操作的输入，第四层的卷积层输出直接作为第五层卷积层的输入。Swish-FER-CNNs中使用的池化层全部采用步长为2、尺寸为3 × 3的最大池化(max pooling)操作。每次池化操作都能减少二分之一的特征参数，提取有效信息、避免过拟合现象。第三层池化层后输出的特征图大小为5 × 5 × 64，输出连接到第一层全连接层上，全连接层的输出大小为1 × 1 × 2048，此过程的丢弃率为0.45，意味着全连接层中的神经元有0.45的概率不参与迭代，能有效防止过拟合现象。经过两层全连接层，最后使用softmax层分类得到的输出尺寸为1 × 1 × 7，对应于7类表情标签。具体的改进的网络结构如表1所示。

Table 1. Swish-FER-CNNs network architecture

表1. Swish-FER-CNNs网络结构

相比Jeon的深度学习模型，Swish-FER-CNNs网络模型多次使用了级联的两层3 × 3的卷积层替代Jeon使用的5 × 5卷积层，加深了网络的层数，尺寸较小的过滤器可提取细化的特征，每层卷积后均激发Swish函数，使整体网络的激活函数频数增加，网络的非线性拟合能力增强。

3. 数据集

实验采用的数据集为kaggle人脸情绪识别数据集——fer2013，该数据集由Pieere和Aaron在ICML2013研讨会上发布，共由35887张人脸情绪图片组成。其中，生气的表情有4953张，厌恶547张，恐惧5121张，高兴8989张，悲伤6077张，惊讶4002张，中性6198张。数据集由三个部分组成，第一部分为训练集，包含28,709张图片。第二部分为验证集，包含3589张图片。第三部分为测试集，包含3589张图片。

4. 实验分析

实验使用caffe [20] 的深度学习框架，操作系统为ubuntu16.04，GPU为GTX1050Ti。训练的学习率为0.001，动量为0.9，学习策略为SGD。Swish-FER-CNNs模型开始迭代后，测试准确率开始逐步增加，测试误差逐步下降，之后趋于平稳，这说明模型的准确率达到模型的饱和状态，训练迭代次数选择合理。训练完成后，测试集准确率达到74.76%，测试误差收敛到0.3168。训练过程如图4、图5所示：

Figure 4. Training accuracy

图4. 训练准确率

Figure 5. Training loss function

图5. 训练损失函数

采用训练好的模型对测试数据集中各个类别的情绪图片进行批量识别。可得到第i类情绪图片中正确识别的个数，记为TP_i，余下的为错误识别个数，记作FN_i。TP_i + FN_i恒等于测试数据集中该类情绪图片的样本总个数Sum_i。7类情绪的测试准确率P_i使用以下公式计算：

$P_i=\frac{T{P}_i}{T{P}_i+F{N}_i}=\frac{T{P}_i}{Su{m}_i}$ (9)

Swish-FER-CNNs学习模型对各类情绪识别的准确率如表2所示。

Table 2. Confusion matrix of emotion recognition accuracy of Swish-FER-CNNs model

表2. Swish-FER-CNNs模型情绪识别准确率混淆矩阵

由于kaggle数据集中各类别的情绪样本不均匀，导致各类样本在模型中的学习数据量不一致。因此，各个类别的分类效果不同。

将Jeon’s深度学习模型分别采用ReLU、L-ReLU、P-ReLU和Swish激活函数，与本文的Swish-FER-CNNs深度学习模型进行对比，结果如图6所示。

Figure 6. Accuracy of test confusion matrix for each model

图6. 各模型的测试混淆矩阵精度

如图所示，分别使用ReLU、L-ReLU、P-ReLU、Swish激活函数，模型识别准确率依前述顺序依次递增。改进后的Swish-FER-CNNs深度模型，相较于使用Swish激活函数的Jeon’s深度学习模型，取得了更高的识别准确率。

为更直接地分析模型的性能，采用准确率ACC表示模型在测试集中识别的准确率，如下所示：

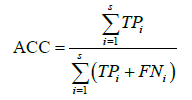(10)

测试集中的人脸情绪分为s种类别，采用 $T{P}_i$ 表示某个类别中正确识别情绪的个数， $F{N}_i$ 表示该类别错误识别的个数。各方法识别情绪的准确率如表3所示。

Table 3. Comparison of recognition accuracy

表3. 识别准确率对比

由表3可以看出，经过充分的迭代，在Jeon’s深度学习模型下，不同激活函数的识别准确率为：ReLU < L-ReLU < P-ReLU < Swish，因此Swish激活函数性能优于前三者。此外，Swish-FER-CNNs网络模型与基于Swish等激活函数的Jeon’s深度学习模型相比，具有更高的识别准确率。

5. 结束语

本文研究了激活函数的性能和网络结构的特性，采用性能优良的Swish激活函数改进反向传播算法，并使用能够提取细化特征的多层小尺寸卷积模块，改进了网络结构，构建了人脸情绪识别深度学习模型Swish-FER-CNNs。新模型是一种自动提取人脸情绪特征的深度学习算法，提高了人脸情绪识别的准确率。模型的训练时间仍然可以通过改进激活函数进行优化，这将是下一步的研究方向。Swish激活函数中参数α的取值对模型性能有较大的影响，这可作为优化模型的另一个方向。

基金项目

本研究获得国家自然科学基金(NO.61771414)项目资助。