1. 引言和准备
称半群S为右主投射半群(简称rpp半群),如果对于任意的
,作为S1-系,aS1总是投射的。对偶地,定义左主投射半群(lpp半群)。作为完全正则半群(completely regular semigroup)的推广,郭聿琦,岑嘉评,朱聘瑜 [1] 定义了强rpp半群(strongly rpp semigroup)。之后,有一系列论文从事这一课题的研究(参见, [2] - [22] )。类似于密码群(cryptogroup),郭小江,杨艳萍 [12] [20] 定义了密码rpp半群(cryptic rpp semigroup),并且给出了这类半群的结构。同余理论是半群理论的重要组成部分,同余性质可以很好地表达半群的结构信息,因此研究半群上的同余是有意义的。本文将考虑密码rpp半群的同余问题。事实上,对密码rpp半群的同余理论,已经做了些探索(见 [8] )。
作为通常Green-关系的推广,我们有
众所周知,
为右同余,
为左同余。一般地,
,
。但当a,b都是正则元时, 当且仅当
。等价地,半群S为rpp半群当且仅当对于任意的
,都存在幂等元e使得
当且仅当
。等价地,半群S为rpp半群当且仅当对于任意的
,都存在幂等元e使得 。易知,正则半群是rpp半群。
。易知,正则半群是rpp半群。
定义1.1:一个rpp半群S称为强rpp半群(strongly rpp semigroup),如果对于任意的
,都存在惟一幂等元
,使得
且
。
对偶地,定义强lpp半群(strongly lpp semigroup)。为更好地研究强rpp半群,郭小江,郭聿琦,岑嘉评 [5] [6] 定义了如下关系。令S为强rpp半群,
,定义
郭小江,郭聿琦,岑嘉评证明了:
1)
;
2)
;
3) 对于任意的正则元
,
。
一般地,
不是S上的左同余。如果
为S上的左同余,则称S为超rpp半群(super rpp semigroup) (见 [6] )。事实上,一个强rpp半群为超rpp半群的充分必要条件是它上的
关系为半格同余。
定义1.2:强rpp半群S称为密码rpp半群(cryptic rpp semigroup),如果
为S上的同余。finition
郭小江,杨艳萍 [12] 指出:密码rpp半群都是超rpp半群,并且密码群恰为正则的密码rpp半群。关于密码群,参见 [23] )。叶火平,郭俊颖,郭小江 [21] 证明了:一个超rpp半群的所有正则元构成一个完全正则半群。这表明,一个密码rpp半群的所有正则元构成一个密码群。
定义1.3:半群S上的同余
称为
-同余(
-congruence),如果对于任意的
,
蕴含着
。
定义1.4:强半群S上的同余
称为酉同余(unary congruence),如果对于任意的
,
蕴含着
。
引理1.5 ( [8] ,引理7):令S为强rpp半群。若
为S上的
-酉同余,则
为强rpp半群,且
, 。
。
本文将采用教科书 [24] 的概念和术语,未给出定义的可参见文献 [6] 。
2. 迹
本节将研究密码rpp半群上同余的性质。首先,回忆同余迹的定义。
定义2.1:令S为半群,
为S上的同余。称E(S)(S的幂等元集)上的等价关系
为同余
的迹。
为得到密码rpp半群同余迹的一般性质,引进如下概念。
定义2.2:E(S)上等价关系
称为正规的(nomral),如果
(T)
进一步,E(S)上的正规等价关系
称为真的(proper),如果
既不为恒等关系
,也不是泛关系
。
明显,E(S)上的恒等关系
和泛关系
都是正规的。记JN(S)为E(S)上所有正规等价关系所组成的集合,并赋予集合的包含关系。
据定义,不难验证,有如下推论:
推论2.3:E(S)上的正规等价关系的交还是正规的。
基于推论2.3,可以证得下面引理。
引理2.4:关于如下运算:对于
是完备格。
证明:据推论2.3,
与
均为E(S)上的正规等价关系。因此
和
都是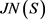 上代数运算。据此,易知:
为一个完备格。
上代数运算。据此,易知:
为一个完备格。
下面是本节的主要结果。
定理2.5:令S为密码rpp半群。对于E(S)上的等价关系
,以下各款等价:
(i)
为正规的;
(ii)
,其中
为含于
的最大同余;
(iii) 存在S上的
-酉同余
,使得
;
(iv)
,其中
为包含
的最小
-酉同余。
而且,如果条件(i)~(iv)满足,那么S上以
为迹的
-酉同余均包含在区间
。
证明:(i)⇒(ii)显然,
为自反的,对称的。令
且
,则存在
使得
。而
,进而
,因此
,故
。
这样,
为传递的。
记
。令
,则对于任意的
,
,进而
,从而
,显然
,反之,若
,则
,进而存在
使得
,从而
。但一个H-类最多含有一个幂等元,从而
,故
,这样
。现在证明了:
。
(ii)⇒(iii)。用(i)⇒(ii)证明中的符号,仅需证明:
为
-酉同余。
令
,由
,知
。对于任意的
,
1) 若
,即
,则对于任意的
,
,从而存在
使得
。但
为S上的同余,于是
。
因此
。
2) 若
,则
,再根据(1),有
综合(1),(2),已经证明了:对于任意的
,
从而
,故
为
-同余。
设
,那么
使得
,进而
,于是
,从而
,
,因此
。故
为酉同余。
(iii)⇒(iv)。明显,
,进而
。若
,则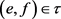 ,从而
,这样
,故
。
,从而
,这样
,故
。
(iv) ⇒(i)。因为
对于任意
(由于
为酉同余)
所以
为正规等价关系。
现在假设条件(i)~(iv)成立。令
为S上的
-同余,且
,则
。对于任意的
,且
,由
,从而
,因此
,进而
。反之,若
,则由条件(ii),(iv),
故
。
3. 几类L*-酉同余
本节考虑密码rpp半群上的几类重要同余。
半群S上的同余
称为幂等元分离(idempotent-separating),如果对于任意
,
蕴含着
。等价地说,
为幂等元分离同余的充分必要条件是
(E(S)上的恒等关系)。
命题3.1:令S为密码rpp半群,
为S上的
-酉同余,则
为幂等元分离同余的充分必要条件是
。
证明:(充分性)设
。对于任意的
,若
,进而
,从而
,故
为幂等元分离同余。
(必要性)设
为幂等元分离同余,那么
,据定理2.5,
。
半群S上的同余
称为左消幺半群同余(left cancellative monoid congruence),如果
为左消幺半群。不难验证,对于rpp半群,任一左消幺半群同余都是
-酉同余。
命题3.2:令S为密码rpp半群,
为S上的
-酉同余,则
为左消幺半群同余的充分必要条件是
。
证明:设
为左消幺半群同余,则
有且仅有一个幂等元。易知,对于任意的
,
是
的幂等元,因此
,故
,于是
。
反之,若
,则根据引理1.5,
有且仅有一个幂等元。因此
为幺半群。但
为强rpp半群,所以
为左消幺半群,故 为S上的左消幺半群同余。
为S上的左消幺半群同余。
下面是命题3.2的直接推论。
推论3.3:令S为密码rpp半群,则
是S上的最小左消幺半群
-酉同余。
Rpp半群S称为C-rpp半群,如果E(S)在S的中心内。等价地,一个半群为C-rpp半群的充分必要条件是它为一些左消去幺半群的强半格。值得指出,一个C-rpp半群的所有正则元构成一个子半群,并且为Clifford半群(即,所有幂等元都在其中心的正则半群)。关于Clifford半群,参见( [24] , p. 93)。
半群S上的同余
称为S上的C-rpp半群同余,如果
为C-rpp半群。
引理3.4:令S为密码rpp半群,
为S上的
-酉同余。对于任意的
,若
,则
。
证明:由定义,知
,于是
。据引理1.5,
,
。因此
,从而
。
命题3.5:令S为密码rpp半群,
为S上的
-酉同余,则
为C-rpp半群同余的充分必要条件是
。
证明:(必要性)设
为C-rpp半群同余,若
,于是存在
使得
,从而
。但
的所有正则元组合Clifford子半群,所以
,因此
。反之,记RegS为S的所有正则元组合的集合。由S为密码rpp半群,知S为超rpp半群,于是RegS为完全正则子半群,易知,
为RegS上的Clifford半群同余,再据( [23] , p. 257, Exercises VI.2.13(i)),
。若有
,显然,
,于是
,从而
。故
。
(充分性)假设
。注意到,RegS为密码群,再根据引理1.5,要证
为C-rpp半群,仅需证:
为Clifford半群。又
蕴含着
,再由( [23] , p. 257, Exercises VI.2.13(i)),
为Clifford半群。从而
为C-rpp半群,即
为C-rpp半群同余。
基金项目
国家自然科学基金项目(11761034, 11361027, 11661042)和江西省自然科学基金项目(20161BAB201018)资助。