基于GA的狭小施工场地平面布置优化研究

GA-Based Optimization of Plane Layout of Narrow Construction Site

摘要: 地铁、城市道路等市政工程施工，大都处于城市闹区，施工场地往往受既有建筑物的制约，且地铁施工场地区域往往狭小拥挤，场内设施的布置往往受到较大的制约，导致施工场地内的施工流通不畅，因此科学合理地对施工场地进行布置显得尤为重要。本文以某市地铁车站一期一阶段场地平面布置为例，结合LEC评价法和施工现场条件构建场地布置数学模型，同时借助遗传算法全局寻优的特点，求解得出最优场地布置方案和场地设施尺寸。

Abstract: Municipal construction projects such as subways and urban roads are mostly located in urban downtown areas. Construction sites are often restricted by existing buildings, and subway con-struction sites are often narrow and crowded. The layout of on-site facilities is often constrained by large restrictions, resulting in construction sites. The construction of the construction is not smooth, so it is particularly important to arrange the construction site scientifically and reasonably. Taking the plane layout of the first phase of a city subway station as an example, this paper combines the LEC evaluation method and the construction site conditions to construct the mathematical model of the site layout. At the same time, the optimal site layout scheme is obtained by means of the global optimization characteristics of the genetic algorithm.

1. 引言

近年来，城市轨道交通因为其便利性和高效性得到了大力发展，相关协会数据显示，截至2018年底，我国大陆地区共有35个城市开通城市轨道交通运营线路185条，运营线路总长度5761.4 km [1] 。同时高强度、快速度的建设也带来了严峻的施工安全问题，地铁施工作为典型的狭小施工场地，其安全问题十分突出。相关地铁施工事故统计资料显示，自2011年以来，地铁施工事故数量尽管比较于往年有所降低，但是却呈现出不断上涨的态势，死亡比率总体上与年份总数成正比，随着事故数量的增加而增加 [2] 。而地铁施工场地平面布置作为工程建设的基础，在人员、物料安全流动过程中起着重要的作用，因此对施工场地的平面布置进行优化研究，能够有效地保证工程活动在低风险水平下实现最高效化的工程建设。

在施工场地的平面布置优化研究中，周友海 [3] 运用目标规划的方法，以钢筋加工场地和混凝土搅拌机为对象构建方案设计的数学模型，最后以图解形式得出场地布置的优化方案。宋兴蓓 [4] 提出基于BIM技术的动态场地布局模型，并借助系统布置设计方法分析设施之间的密切程度，建立动态布局模型的目标函数，并借助群智算法进行优化。李伟 [5] 根据功能分析，将地铁施工场地划分。为施工区、机械设备停放区等单元，采取系统布置设计方法分析单元之间的物流与非物流关系，最后得出施工场地的优化布局方案。刘文涵 [6] 借助系统布置设计理论中物流分析方法构建施工现场平面布置安全模型并通过蚁群算法寻优求解，最终得出高安全水平下的场地布置方案。上述研究均具不同程度的实现场地平面优化布置的目标，但在如何保持低风险水平下的高效率工程建设的问题上却没有涉及。

因此，本文提出将安全评价中常用的半定量分析法——LEC评价法引入场地平面布置的数学模型中，将LEC乘积所得到的风险值D作为模型目标函数，并借助施工现场条件构建相应的约束函数，最后应用遗传算法对该模型进行寻优求解，得出低风险水平下高效施工建设的场地布置优化方案。本文实施步骤如图1所示。

2. 施工场地概况

某市地铁车站围挡图如图2所示。围挡内主要进行地连墙作业，场内布置的临时设施主要是原材堆放场和钢筋加工场，钢筋加工场的面积为240 m²，原材料堆放场的面积为60 m²。对施工现场进行分析发现原场地布置存在以下两个问题：

Figure 1. Program implementation steps

图1. 方案实施步骤

1) 施工平面布置与实际不符。施工平面布置参照过往工程的布置方案，未做到真正符合现场实际来进行平面布置，同时，在施工过程中，施工单位会根据实际的施工需要临时修改场地布置方案，这无疑会导致施工过程中不确定性的增加，无法真正把控施工全过程中的风险因素，致使施工隐患突增，施工平面布置的真正作用没有得到充分利用。

2) 临时设施布置不合理。在实际施工过程中，临时设施的布置仅凭施工人员的经验进行布置，没有采取科学合理的办法分析现场物料、人员流动之间的安全性和经济性，很容易导致临时设施之间物料运输效率低下，人员流动风险程度较高，进而导致施工效率的低下，增加企业成本的同时也没有控制住施工现场的安全水平。

Figure 2. Constructional layout

图2. 施工平面布置图

3. 施工现场平面布置优化

3.1. 施工场地布置模型

本文采用数学模型建模的方式进行模型构建，以图2中的施工场地布置为例，建模的对象主要考虑钢筋加工场、原材料堆放场的储存问题，因此以钢筋笼加工场的钢筋加工量与原材料堆放场的原材堆放量为建模变量。同时引入LEC评价法，LEC评价法是对具有潜在危险性作业环境中的危险源进行半定量的安全评价方法 [7] 。

L为发生事故的可能性大小；E为人体暴露在这种危险环境中的频繁程度；C为一旦发生事故会造成的损失后果。风险分值D = L * E * C。D值越大，说明该系统危险性越大。

为简化计算，将事故发生的可能性、施工人员暴露时间、事故发生后果划分不同的等级并赋值，如表1至表3所示。

Table 1. L value and connotation

表1. L取值及内涵

Table 2. E value and connotation

表2. E取值及内涵

Table 3. C value and connotation

表3. C取值及内涵

3.1.1. 模型变量与目标函数构建

考虑施工现场的地连墙施工的施工效率，钢筋的加工量及原材料堆放量都直接关系到地连墙施工效率。因此设置每周应加工的钢筋加工量为X₁个单位，每三天应储存的原材堆放量为X₂个单位。参照现场施工资料与相关风险评估报告，施工现场每周应加工的钢筋加工量为18个单位，每三天应储存的原材堆放量为8个单位。基于此工作任务，施工现场的风险等级为低度(I级)。为保证在最低风险状态下实现最大效率的工程施工，考虑钢筋的加工量及原材料堆放量与LEC评价要素中的关系：

当钢筋加工量增多时，工人的劳动强度增加，误操作的可能性增加，则事故发生的可能性也随之增加；同时原材料堆放量也随之增加时，工人在原材堆放场与钢筋加工场之间活动的频繁程度增加，即暴露在危险环境中的频繁程度增加。鉴于施工场地内存在的主要事故类型为机械伤害，且钢筋加工场的机械对工人的伤害程度通常不会达到致死水准，因此确定本案例施工场所的事故后果水平主要是严重伤残水平。

模型：已知该围挡区域内自行加工钢筋和堆放原材料，以施工现场18个单位钢筋加工量和8个单位原材堆放量为标准，对应分值为L = 0.5，E = 6。对事故发生可能性L来说，每增加一个单位的钢筋加工量，事故发生可能性分值增加0.8；对暴露危险区域频繁程度来说，每同时增加一个单位钢筋加工量与原材料堆放量，暴露于危险环境的频繁程度分值分别增加0.8与1，而考虑到钢筋加工场往往需要工人长时间活动，因此对于暴露于危险环境的频繁程度分值采取线性加权的方法，W₁ = 0.6，W₂ = 0.4。对于事故后果C，参照事故后果水平主要是严重伤残水平，因此取常值C = 7。因此有目标函数。

$D\left(x\right)=L\left(x\right)\times E\left(x\right)\times C$ (1)

$L\left(x\right)$ ：发生事故的可能性大小所得分值；

$E\left(x\right)$ ：为人体暴露在这种危险环境中的频繁程度所得分值；

C：一旦发生事故会造成的损失后果分值；

即： $D\left(x\right)=7\left[\left(x_1-18\right)\times 0.8+0.5\right]\times \left[\left(x_1-18\right)\times 0.8\times 0.6+\left(x_2-8\right)\times 1\times 0.4+6\right]$

3.1.2. 约束条件构建

为保证施工现场的运输效率，减少不必要的运输成本，钢筋加工场与原材料堆放场的距离必须保持一定的距离，应施工方要求，钢筋加工场、原材料堆放场距离地连墙施工区域的距离不得超过15米；由于在增加钢筋加工量与原材料堆放量的同时，风险值对应地上升，因此保证风险值在低度(I级)区间最高值，以便于最大化的利用场地资源。风险区间表如表4所示。

Table 4. Risk classification

表4. 风险等级划分

同时已知增加一个单位的钢筋加工量钢筋加工场地将远离地连墙施工区域的距离为0.2 m，增加堆放一个单位的原材料堆放量原材料堆放场将远离地连墙施工区域的距离为0.5 m，加工一个单位的钢筋占用场地为9 m²，堆放一个单位的原材料占用场地为8 m²。优化后的临时设施占地面积应不超过原有场地布置临时设施的占地面积，因此有约束条件：

$9X_1+8X_2\le 320$ (2)

$0.2X_1+0.5X_2\le 15$ (3)

$D\left(x\right)\le 69$ (4)

$18\le X_1\le 40$ (5)

$8\le X_2\le 40$ (6)

式中： $X_1$ 指每周应加工的钢筋量； $X_2$ 指三天应储存的原材料堆放量。

3.2. 遗传算法优化

遗传算法作为一种全局寻优的迭代算法，其先进性和智能性已经得到了广泛认可。本文借助遗传算法迭代寻优的功能特点，以风险值为目标函数，以相关工程要求、资料为约束条件，求解得出满足低度(I级)最高风险区间值上的钢筋加工量和原材料堆放量以及钢筋笼加工场和原材料堆放场相对于地连墙施工区域的相对位置方案。目标函数和约束条件借助MATLAB工具编译成m文件，经遗传算法工具箱求解。

遗传算法工具箱GUI求解

在matlab2014版本中内嵌有遗传算法工具箱GUI界面 [8] ，交互式操作界面能够极大简化算法的使用流程。在m文件编写完成后，经由GUI界面完成遗传算法中初始种群、迭代代数、交叉概率、变异概率等参数的设定。参数设置如表5所示。

参数与约束条件设置完成后，即可求解得出满足目标区间的最优解。具体如图3所示。在图3中，可行性解从第5代到第45代结束，迭代过程中最佳适应度变化比较平稳，没有出现较大的波动，说明计算结果的精度和稳定性较高。迭代计算到第45代结束时，最佳适应度逼近68.99，此时最佳个体X₁ = 19.2，X₂ = 8.5，即钢筋加工量为每周19.2个单元，原材料堆放量为每三天8.5个单元。经检验得出，该布置方案满足模型中约束条件的要求，说明计算结果具有一定的准确性。优化后的场地布置方案如图4所示。

Table 5. Parameter settings

表5. GUI参数设置

Figure 3. Iterative solution graph

图3. 迭代求解图

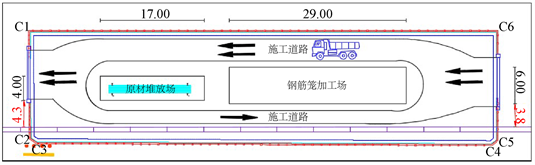
Figure 4. Construction plane optimization layout

图4. 施工平面优化图

在图4中，原材堆放场和钢筋加工场的距离分别距离地连墙施工区域4.3米和3.8米，比较原施工布置图，优化后的钢筋加工场尺寸由原来的长30米宽8米变为长29米宽6米；优化后的原材堆放场由原来的长20米宽3米变为长17米宽4米；在满足工程任务的情况下，钢筋加工场和原材堆放场的尺寸得到了进一步优化，这进一步减少了狭小施工场地内临时设施的占地空间，增强了施工场内人与机的活动空间；同时，施工场地内也形成了一个环形空间，场地道路的环形布置更有利于进场车辆进行物资装卸、吊运以及钢筋笼的吊装等作业，因此说明该布置模型的计算结果具有一定的科学性和准确性。

4. 结论

本文将LEC法引入场地优化布置模型，以风险值为目标函数，以相关施工现场资料为约束条件构建了场布模型，最后运用遗传算法对模型进行迭代求解，得出最终的场布方案，主要的结论如下：

1) 将LEC法引入场地优化布置模型中，通过控制场布方案的风险值，使得场布方案的安全性提高，因此该方法能够为场地布置安全问题提供一些新的解决思路。

2) 依据施工资料，充分挖掘临时设施之间的物流关系信息，使得场地优化布置模型中的约束关系紧贴工程实际，得出的场布方案具有一定的工程实际价值。

3) 利用遗传算法对场地优化布置模型进行全局寻优迭代计算，得出的场布方案结果在符合各项约束条件的同时，得出了理想目标的场布方案，实现了场地平面优化布置的目标。

NOTES

^*第一作者。

^#通讯作者。