1. 引言
拓扑学是数学中一个重要的、基础性的分支,找出给定集合上的拓扑结构一直被认为是比较麻烦的,特别当一个集合包含的元素越多的时候,花费的时间较多,还容易出错。计算机程序设计越来越普遍,一个有效的验证程序在节省验收时间的同时也可以提高准确度。
本文讨论恰含n点的集合的拓扑结构和可能的拓扑的数量,同时给出了验证是否形成拓扑的算法。下文先给出了需要的基础知识。第二部分讨论恰含n个点的集合的拓扑结构,找出了形成的可能拓扑的规律,并通过实例加以说明。第三部分给出了验证X的任意子集族T是否为X的拓扑空间的程序。
2. 基础知识
1) 拓扑空间定义:
定义1.1 [1] :设X是一个集合,
(
表示X的幂集),即T是X的一个子集族,如果T满足如下条件:
1、
2、如果
,则
3、若
,则
,
。
则称T是X上的一个拓扑。
如果是集合X上的一个拓扑,则称对偶
是一个拓扑空间,或称集合X是一个相对于拓扑T而言的拓扑空间;或者当拓扑T早已约定或在行文中已有说明而无需指出时,仅称集合X是一个拓扑空间,此外T的每一个元素叫做拓扑空间
中的一个开集,集合X中的元素叫拓扑空间中的点。
设T是X的一个拓扑,由于T中的每一个元素是拓扑空间X中的开集,因此拓扑空间X的定义可以理解为:
一个集合X的拓扑是X的一个开集族满足条件:
1、
是开集;
2、任意两个开集的交集是开集;
3、任何开集族的并是开集。
注1:
1、X的任意有限开集族的交是开集。
2、X的任意开集族的并是开集。
对偶的我们可以写出闭集的类似定义:
注2:
1、X的任意有限闭集族的并是闭集。
2、X的任意闭集族的交是闭集。
2) 拓扑空间上特殊的空间
1、平庸拓扑:
,T是 X的一个拓扑,称之为X的平庸拓扑,这样的拓扑空间只有一个,在平庸空间中只有两个开集,即X自身和空集,称为最粗的拓扑。
2、离散拓扑:
,即T是由X的全体子集构成的,显然,T是X的一个拓扑,称之为X的离散拓扑,并且称拓扑空间
为离散空间,这样的拓扑空间有一个,称为最细的拓扑。
3、除此之外,我们对
一般的拓扑空间进行探究:
3. 恰含n个点的集合的拓扑结构
根据拓扑空间的定义,我们可以根据集合X中含有不同元素而构造不同的拓扑,在此之中寻找其规律,主要通过以下几个方面做探究:
1、分别设X是一个包含一、二、三、四个元素的集合。
2、当集合X中的元素不同时,可以构造几个不同的拓扑,随着元素的增加,有何规律。
3、当集合X含有的元素不同时,会包含几类不同的拓扑。
4、每一类拓扑之间有何规律。
5、不同的拓扑之间是否有关联。
6、当含有元素为奇数和偶数是是否呈现一致的规律。
1) 主要结论
,X上的拓扑
,T的元中,
,(A是真子集)
可能的个数
种
,T的元中,
Case1:
(即满足
)
,则B的可能个数为
设T的总个数为
Case2:
,T的元中,
Case1:
,在这种情况下,
假设:
则A的取值法
,B的取法
Case2:
,
,
,即
,设 ,
,则A的取法
;B的取法
,总的拓扑的数:
,
,则A的取法
;B的取法
,总的拓扑的数:
C的取法:
,
总的拓扑个数:
;
,T的元中,
Case1:
,
总的拓扑个数
Case2: ,设
设
,设
设
总的拓扑个数为:
2) 例题
例1:X是含有一个元素的集合
,n = 1,则拓扑空间有1个为:
例2:X是含有两个元素的集合
,n = 2,则拓扑空间有3个为:
,
,
例3:X是含有三个元素的集合
,n = 3,则拓扑空间有32个为:
,含有除
外,单个元素的拓扑空间有6个为:
,
,
,
,
,
,含有除
外,两个元素的拓扑空间有9个为:
①
:
,
,
,
,
②
:
,
,
,除
外,含有三个元素的拓扑空间有6个为:
①
or
,
,
,
:
,
,
②
,
,
:
,
,
,除
外,含有四个元素的拓扑空间有6个为:
,
,
,
,除
外,含有五个元素的拓扑空间有3个为:
,
,除
外,含有六个元素的拓扑空间有1个为:
例4:X是含有四个元素的集合
,n = 4,则拓扑空间有:466个
(因为拓扑空间个数较多,我们只写出每一类的代表元)
,含有除
外,单个元素的拓扑空间:14个
(4个)
(6个)
(4个)
,含有除
外,两个元素的拓扑空间:36 + 7 = 43
(36个)
①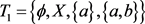 ,
,
,
(各有3个)
,
,
,
(各有3个)
②
,
,
,
(各有3个)
③
,
,
,
,
,
(各有2个)
:
①
②
(各有3个)
,除
外,含有三个元素的拓扑空间有36个为:
(6个):
(24个):
(6个):
,除
外,含有四个元素的拓扑空间有36个为:
(12个):
(12个):
(12)#Math_165#
,除
外,含有五个元素的拓扑空间有22个为:
(16个):
(6个):
,除
外,含有六个元素的拓扑空间有180个为:;
①
,除
外,含有七个元素的拓扑空间有28个为:
(4个):
(24个):
①
(4个)
②
(4个)
③
(4个)
④
(4个)
⑤
(4个)
⑥
(4个)
,除
外,含有八个元素的拓扑空间有84个为:
,除
外,含有九个元素的拓扑空间有12个为:
,除
外,含有十个元素的拓扑空间有4个为:
,除
外,含有十一个元素的拓扑空间有12个
,除
外,含有十二个元素的拓扑空间有0个
,除
外,含有十三个元素的拓扑空间有0个
,除
外,含有十四个元素的拓扑空间有1个为:
根据上面实例我们得到下表数据:
4. 验证是否为拓扑空间的算法
从以上的不同集合上构造不同拓扑可以看出,验证方法特别繁琐,而且当一个集合包含的元素越多的时候,花费的时间较多,还容易出错。计算机程序设计越来越普遍,计算机计算节省了很多时间。下面给出X的任意子集族T是否为X的拓扑空间的程序:



return 0;
}
附程序:

注:此程序是以数值进行输入,所以验证的拓扑空间是自然数的子集族。下面我们以例题的方式验证程序的可行性。
例5:设X是一个三元素集合,
,我们验证X的子集族
和
是否为拓扑空间。


注:
1、依次可验证任意集合上的任意子集族是否为拓扑空间,由于验证界面较长,不在此展示,读者可自行验证。
2、我们给出了定义1.1的验证程序,有兴趣的读者可根据基础知识中的注1和注2写出相应的验证程序。
基金项目
本课题由青海省自然科学基金(批准号:2018-z-911)、国家自然科学基金(批准号:61773019)资助。