1. 引言
传统的化石能源自工业革命开始以来就处于消耗大于再生的状态,结合当代中国乃至世界的飞速发展的现状,在未来的十几年甚至几年之内,传统化石能源势必日渐式微,难以持续供给,因此减少对于传统化石能源的依赖,加大对于新能源的研究和开发是目前为止较为适宜的能源持续拓展使用的方法 [1] [2] [3] [4] 。针对这一问题,ITER以及CFETR计划诞生,着力解决新能源储存与使用问题。在两个计划当中,氢以及氢的同位素储存在整个计划当中有着非常重要的作用,而设计合理的金属氢化物储氢床是解决这个问题的关键,经过多年的国内外学者的研究开发和优化,双薄壁同心管状床成为目前正在使用的储氢床设计 [5] - [10] ,如图2所示。
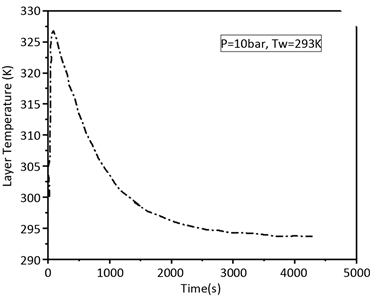
S. Mellouli,F. Askri,H. Dhaou等 [6] 学者的研究中,通过实验详细地记录了金属氢化物储氢床吸氢过程中整个储氢床的温度和压力随时间的变化情况,如图1所示,在冷却液初始温度Tw = 293 K,床体初始氢压P = 10 bar的条件下,整个反应过程从开始到结束时的最大温差ΔT = 32.5 K,最大压力差ΔP = 8 bar,金属氢化物储氢床在此加载条件下反复循环使用,氢化物的形成不断地改变床体内部的氢压,形成的循环载荷持续地施加在床体内部,因此作为床体的主要结构材料——316L (N)不锈钢的蠕变–疲劳寿命评价预测直接关系到整个床体乃至整个储氢系统的安全性评定。
 (a)
(a) 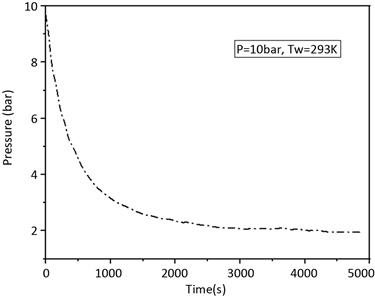 (b)
(b)
Figure 1. The measured temperature and pressure curve of the bed body change with time; (a) Curve of bed temperature over time; (b) Curve of bed pressure over time
图1. 床体实测温度、压力随时间变化曲线 [6] ;(a) 床体温度随时间变化曲线;(b) 床体压力随时间变化曲线
Hyun-Goo Kang,Eun-Seok Lee,Seungyon Cho等 [3] 经过模型改进后提出图2的新型金属储氢床,在此储氢床中,316L (N)不锈钢是被用于承接冷却通道的介质,其作用在于将储氢过程中反应放出的热量从储氢层(即图中ZrCo层)带走,同时将热量传递给冷却通道中的冷却介质,从而达到降低床体温度、提高吸氢效率的目的。因此,进一步说明316L (N)不锈钢的存在对于双薄壁同心管状床整体意义重大,保证316L (N)不锈钢的安全性能是保证该床体整体安全的首要任务。本文工作内容即为通过实验找出可能影响材料疲劳寿命的因素,并利用已得到的实验数据利用人工智能中的BP神经网络进行预测,一方面验证BP神经网络的正确性和精准性,并根据预测结果得到影响316L (N)不锈钢疲劳寿命的关键因素和机制;另一方面,确定BP神经网络的可行性,利用人工智能——BP神经网络的工作特性,在预测工作中只要有大量的基础数据做铺垫即可以对任意参数进行预测,并且用此方法避免了传统预测模型方法中参量取值的复杂性 [11] 。
1、疲劳寿命预测模型
1) 模型一——Basquin-Coffin-Manson公式
其中,εa——总应变幅;
——弹性应变幅;
——塑性应变幅;
E——弹性模量;
——疲劳强度系数疲劳强度指数;
B——疲劳韧性指数;
c——疲劳韧性指数;
2Nf——疲劳寿命。
此模型为预测的基本模型,
、b、
以及c根据不同材料对应不同的取值,如表1所示。该模型的优势为已知参数较多,最终形成应变幅εa与材料的疲劳寿命2Nf一一对应的函数关系,整体模型简单清楚。然而在此模型之中影响材料疲劳寿命的影响因素仅考虑了应变幅,根据实验结果表明影响材料疲劳寿命的因素存在多种可能,因此考虑此模型的使用存在一定局限性。

Table 1. 316L (N) prediction model parameter value
表1. 316L (N)不锈钢的预测模型参数取值
2) 模型二——SWT模型
基于Basquin-Coffin-Manson公式,建立SWT模型:
此模型为优化Basquin-Coffin-Manson公式得来,在保持其原有的优越性之外,引入了σmax参量,将σmax和εa作为预测疲劳寿命的影响参数,相比Basquin-Coffin-Manson模型此模型考虑影响因素更为完备,由于此模型是基于Basquin-Coffin-Manson公式得到,因此其他相关参数取值与Basquin-Coffin-Manson公式中的一致。
3) 模型三
根据以上模型的预测机理,D. Kujawski,F. Ellyin,Int. J.等 [13] 提出了一个新的模型:
在此模型中,
可以表示为:
(1)
对于316L (N)不锈钢材料,在σm = 50 MPa和σa = 250 MPa的条件下,此模型可以具体写为:
(2)
此模型中直接引入了平均应力σm和塑性应变幅
,且(1)式中的参数可以通过平均应力实验的单一荷载加载条件所测得,c取值与Basquin-Coffin-Manson公式中的一致。(2)式即为Xuyang Yuan等人在σm = 50 MPa和σa = 250 MPa的条件下,得到的最终新模型的计算模型形态。显然,在此模型中对疲劳的影响寿命因素为平均应力σm、应力幅σa以及塑性应变幅εpa。
2. BP神经网络算法及疲劳寿命预测
2.1. BP神经网络算法中的归一化处理技术
BP神经网络为模拟人类大脑结构和功能的智能算法,可以以任意的精度逼近任意连续函数,同时它是一个非线性的动力学系统,因此其特色在于信息分布式储存和并行协调处理。基于其工作特性,BP神经网络可以无须提前描述其数学方程的储存大量映射关系(多输入—多输出),遵循最速下降法的学习规则,根据已得出结果的反向传播(Back Propagation)来不断的调整自身系统的权值和阈值,进而使网络的误差平方和达到最小值 [14] [15] ,BP神经网络模型和神经元的一般模型图如图3和图4所示。
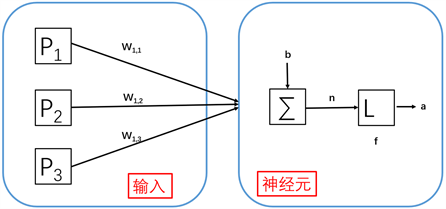
Figure 4. General model diagram of neurons
图4. 神经元的一般模型图
BP神经网络的学习过程和步骤为:
1) 初始化网络
将大量无序的原始数据进行整理归类,明确输入层和输出层数据并区别开来,输入进输入层。
2) 归一化处理
归一化处理一共两种方法,其中一种为把原始数据通过相关公式化为(0,1)之间的小数,另一种为把原始数据里不同量纲的数据通过相关公式将其化为无量纲表达式。归一化处理的主要目的是为了统一原始数据,方便数据处理,因此将原始数据全部映射到(0,1)范围内进行分析处理,使模型建立和数据预测更加快速方便,其实际的数据处理方式应归类在数字信号处理的范围。
两种常用的方法包括:
① Min-Max标准化(Min-Max Noremalization)
Min-Max标准化又称之为离差标准化,其本质在于对原始数据进行线性变化,进而使结果的值映射在(0,1)之间,具体转换函数如下:

其中:
max-样本数据最大值;
min-样本数据最小值;
x-任意样本数据。
一般来说,对于一般的工作量不大的原始数据可用该方法处理,但对于工作量较大的样本原始数据集合,采用此方法时,当有新数据加入时,会有max和min的取值变化的可能,因此方程式此时需重新定义。
② Z-score标准化方法
此方法的核心在于给出初始数据的标准差(standard deviation)和均值(mean),以这两个标准进行数据的标准化。因此,经过此方法处理,处理后的数据均满足标准正太分布,即标准差等于1。均值等于0。相关转化函数为:
其中:
μ——所有初始样本数据的均值;
σ——所有初始出具样本的保准差,表达式为:
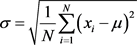
x——任意样本数据。
3) 网络训练
将处理后的数据进行训练,此步骤为神经网络的核心步骤。
4) 判别训练能否收敛或者权值阈值可否达到局部最小
权值在计算机数据结构领域的定义不同于数学领域里“加权平均数中每个数出现频次”的定义,具体在神经网络里,权值是在计算树或者计算图的两个结点路径上从一个结点到另一个结点的相关数据值。
阈值的定义与一般阈值的定义基本相同,一般阈值指的是一个“效应”能够产生的最低值或最高值,这里的阈值具体是指结点传递过程中的标准界定。
5) 满足4)要求时,传递给隐藏层进行计算预测,不满足4)要求时,需更改初始权值阈值,重新进行训练。
6) 得到预测值,与实际值进行对比。
具体运行步骤如图5。
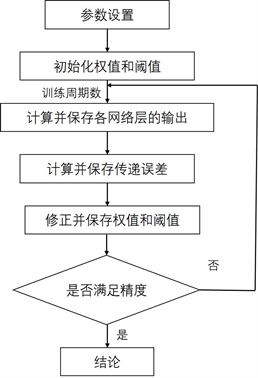
Figure 5. Operation steps of BP neural network
图5. BP神经网络运行步骤
2.2. 储氢床316L (N)不锈钢疲劳性能
在现阶段作为ITER以及CFETR中主要使用的金属氢化物床床体的外壳,其稳定性及寿命监测系统在气体储存环节乃至整个系统的安全运行都非常重要。如表2所示,Xuyang Yuan,Weiwei Yu,Sichao Fu等人 [12] 的实验工作结果,记录了不同循环载荷作用下,不同应变幅、塑性应变幅、应力幅以及平均应力四个因素对该材料的寿命的影响。


Table 2. The measured results of low cycle fatigue life of 316L (N) steel under different control models
表2. 316L (N)不锈钢在不同控制模型下的低周疲劳寿命实测结果 [12]
2.3. 非对称载荷疲劳试验结果分析
如图6(a)所示,滞后环的两个周期的应变间隙随着平均应力的增加而增大,即循环应变幅εa随着平均应力的增加而增大,此时棘轮应变也随着平均应力的增加而增大,同时随着循环周次的增加,循环应变幅εa减少,因此当应力幅一定时,平均应力水平增加,使得循环应变越大,材料获得循环强化,寿命延长,但如图6(b)所示,棘轮应变在此情况下持续增加,材料的疲劳寿命随着棘轮应变的增加而缩短。因此认为316L (N)不锈钢的疲劳寿命的影响因素应存在平均应力与棘轮应变的竞争机制。
 (a)
(a) 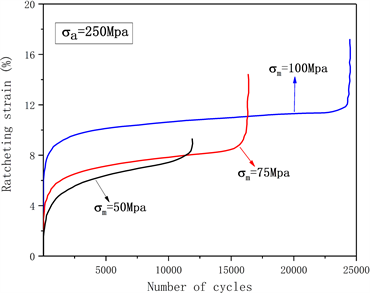 (b)
(b)
Figure 6. Stress-strain hysteresis loop and ratchet strain diagram under asymmetric loads; (a) Stress-strain hysteresis loop (σa = 250 Mpa); (b) Evolution of ratchet strain (σa = 100 Mpa)
图6. 非对称载荷作用下的应力–应变迟滞回线和棘轮应变变化图 [12] ;(a) 应力–应变迟滞回线(σa = 250 Mpa);(b) 棘轮应变变化图(σa = 250 Mpa)
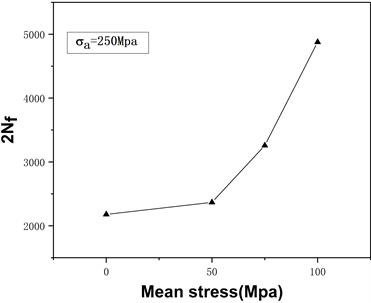
如图7(a)所示,在σa = 250 Mpa的固定应力幅值的非对称应力作用下,材料的疲劳寿命随平均应力的增加而增加,同样的,如图7(b),在此情况下的棘轮应变随平均应力的增加而增加。图7所示的实验结果表明:非对称应力工况下,材料循环强化对疲劳寿命的延长强于棘轮应变引起的寿命缩短,导致非常重要的实验结果,即,材料的疲劳寿命随着平均应力的增加而增加的结论。一方面随着平均应力的增加棘轮应变明显增加,棘轮应变不利于疲劳寿命;另一方面平均应力的升高导致应力应变迟滞回线中循环应变幅减小,这种现象可解释为材料循环强化的结果,有利于疲劳寿命延长。正如文献 [12] 所叙述,非对称应力工况下的寿命预测,从理论上是平均应力提高的强化和Ratcheting引起的应变对寿命影响的竞争。客观上讲:非对称应力工况下,循环应变幅和Ratcheting应变的本构描述要求精度高,这也是对复杂载荷作用下疲劳寿命预测的难点 [12] 。
 (a)
(a) 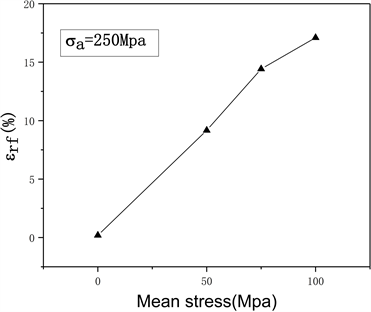 (b)
(b)
Figure 7. The change curve of fatigue life under asymmetric load and ratchet strain; (a) Fatigue life corresponding to different mean stress (b) Ratchet strain corresponding to different
图7. 非对称载荷作用下的疲劳寿命变化曲线和棘轮应变 [12] ;(a) 不同平均应力对应的疲劳寿命;(b) 不同平均应力对应的棘轮应变
2.4. 基于BP神经网络算法预测不锈钢在循环载荷下的疲劳寿命预测
在非对称载荷作用下的疲劳试验中,控制量为平均应力和应力幅值。因此影响因素选取为:平均应力和应力幅值,隐藏层采用2层,输出层即为疲劳寿命2Nf,整合训练组列表为:

Table 3. BP neural network input/output layer Settings
表3. BP神经网络输入/出层设置
按照表3设置得到预测结果,如图8(a),图8(b)所示,预测值非常接近实际观测值,所有控制模型下的点均落在1.5倍分散带内,充分说明了BP神经网络的准确性,同时如图8(c),图8(d)所示,对比Xuyang Yuan以SWT模型预测的回归线结果可知,运用BP神经网络预测得到的结果与实测值更为接近。根据BP神经网络的预测结果及实验测得的结果,如图6所示,在非对称循环载荷作用下,平均应力提高的所引起的材料硬化对疲劳寿命的影响是有利的,但棘轮应变所引起的对疲劳寿命的影响是不利的,因此认为316L (N)不锈钢的疲劳寿命的影响因素应存在平均应力与棘轮应变的竞争机制。
 (a)
(a)  (b)
(b) 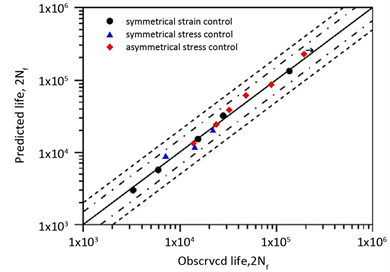 (c)
(c)  (d)
(d)
Figure 8. BP neural network prediction results and comparison; Comparison of BP neural network prediction results; (b) Comparison of predicted and experimental life of BP neural network prediction; (c) Comparison of predicted and experimental life of SWT model; (d) Comparison of the predicted life of the model 3 with the experimental life
图8. BP神经网络预测结果及对比;(a) BP神经网络预测结果;(b) BP神经网络预测寿命与实验寿命的比较;(c) SWT模型预测寿命与实验寿命的比较 [12] ;(d) 模型三预测寿命与实验寿命的比较 [12]
在图8的预测工作中得到的运行图、参数设置以及结果收敛图如图9。
图9(a)、图9(b)表示预测在1166步达到最优值,因此停止训练得到结果,图9(c)为训练过程的收敛图,Gradient是在网格训练中的一个参照函数,采用的方法为梯度下降法;根据Gradient函数的反馈,得到Mu的权值误差调整范围,即迭代过程中的误差范围,迭代过程中误差增加,则Mu的值增加,即Mu∝Error。故当Mu的值和Gradient函数在小范围内出现循环震荡现象时,表明此时误差在可接受范围,完成网格的训练过程。
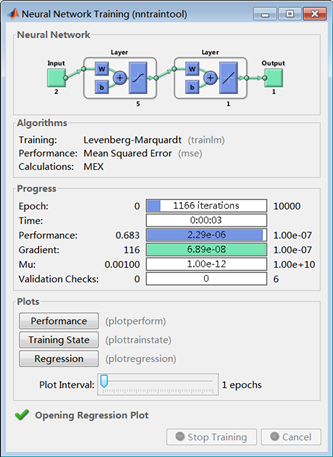 (a)
(a) (b) (c)
(b) (c)
Figure 9. Parameter setting and result convergence diagram; (a) Parameter setting diagram; (b) Error mean square convergence graph; (c) Other resultant graphs
图9. 参数设置及结果收敛图;(a) 参数设置图;(b) 误差均方收敛图;(c) 其他结果图
Validation Checks为用training训练时,每进行一次训练,系统都会自动输入validation set中的样本数据至神经网络以进行验证,而输入validation set后将得到一个误差,值得注意的是,此误差并非网络训练时的误差,而是验证样本数据输入后得到的误差,为输出误差,同时之前对validation set在操作时会设置一个具体步数,如设置8echo,系统则会自动判断在之前所说的生成的误差是否在8次检验后不下降,如果上升或者不下降,则认为training set训练过程中的误差已达到极限,此时没有继续训练的必要,因此停止训练。简单的来说,该值在训练过程中出现上升或者不下降的趋势时,认为网络训练成功。
由于此模型采用的输入层为最大应力值和应变幅幅值,其中最大应力值来源于应力幅值和平均应力值之和,因此在同一应变幅值情况下的不同平均应力和应力幅值对316L (N)不锈钢的疲劳寿命影响敏感度还不清楚。针对这一工作盲区,根据Masayuki Kamaya, Masahiro Kawakubo [16] 的工作,如图10所示,在应变控制模型下,应变幅相同时,应力幅值、最大峰值应力和平均应变值的大小对疲劳寿命的影响不大,但在此条件下施加平均应力会导致寿命缩短;相反,应力幅相同时,施加平均应力可以延长疲劳寿命,如图11所示。
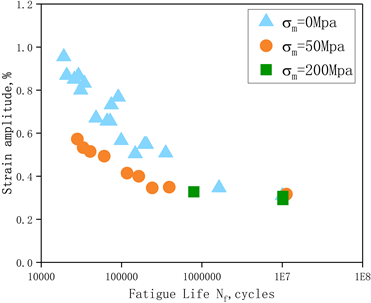 (a)
(a) 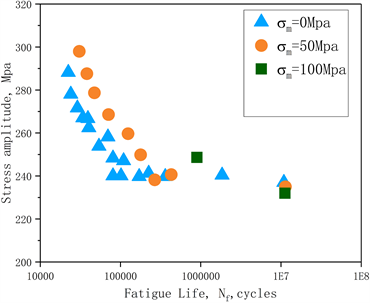 (b)
(b)
Figure 10. Fatigue life under different stress/strain amplitude; (a) Fatigue life under different stress amplitude; (b) Fatigue life under different strain amplitude
图10. 不同应力/变幅值作用下的疲劳寿命 [16] ;(a) 不同应力幅值作用下的疲劳寿命;(b) 不同应变幅值作用下的疲劳寿命
在先前的预测工作中为了对比SWT等传统本构模型的预测结果,将平均应力σm和应力幅值σa考虑成为一个因素,因此为了研究相同应变幅值作用下的平均应力σm和应力幅值σa两者具体对疲劳寿命影响的敏感度,根据Masayuki Kamaya [16] 等人的实验结果,取与表3中应力循环作用下相同平均应力和应力幅值的9个点,得到表4,以平均应力和应力幅值为输入层,疲劳寿命为输出层,利用BP神经网络预测对疲劳寿命的影响。

Table 4. Fatigue life under different stress amplitude and average stress
表4. 不同应力幅值、平均应力作用下的疲劳寿命 [16]
如图11所示,得到的预测结果与实验值非常接近,在应变控制模型下的点均落在2倍分散带内,根据此结果,一方面可以看出在此模型下选用应力幅和平均应力作为影响因素预测得到的结果准确,另一方面可以看出利用同样的BP神经网络模型对不同数据类型的预测精度同样很高,并且在此方法下,没有涉及到本构模型方法里的相关知识,可以以任意的相关参数为输入层对材料的疲劳寿命进行预测,成功的为今后的材料的蠕变–疲劳寿命预测提供了新的思路和方法,以及一定程度上证明了BP神经网络的正确性和精确度。
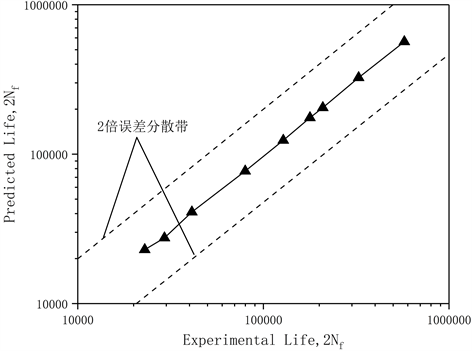
Figure 11. Comparison of predicted life and experimental life under different mean stress and stress amplitude
图11. 不同平均应力和应力幅值条件下预测寿命与实验寿命的比较
在蠕变寿命方面,张莉 [17] 等人研究了对316L (N)不锈钢在550℃的温度下施加不同的加载条件,并对其蠕变疲劳寿命进行研究,记录了应力控制条件下316L (N)不锈钢的蠕变疲劳实验结果,如表5所示。

Table 5. BP neural network input/output layer Settings
表5. BP神经网络输入/出层设置
实验和BP神经网络的预测结果表明,以蠕变疲劳寿命最长时的应力幅(167.5 Mpa)为界线,应力幅值小于167.5 Mpa时,316L (N)不锈钢的蠕变寿命随着平均应力的增加而缩短,而应力幅值大于167.5 Mpa时则与之完全相反。因此,为了充分证明此结论的正确性,还需大量的数据作为基础,利用本文提出的BP神经网络进行相关工作可以有效的节约工作成本和迅速的得到大量数据。现以应力幅值和平均应力值作为输入层,蠕变寿命作为输出层,对现有的7组数据进行预测对比,预测结果如图12,预测结果与实验结果非常吻合,所有点均落在2倍分散带内,表明BP神经网络工作的准确性,因此利用BP神经网络工作的特性,基于大量的网络训练数据,即可实现预测任意应力幅和平均应力下的蠕变疲劳寿命,同时对于实验数据组出现的应力幅分界线167.5 Mpa,可以利用BP神经网络补全数据,对此分界线前后蠕变疲劳寿命的变化趋势进行更深度的规律分析。此外,结合先前对于材料的疲劳寿命预测的工作,本文认为BP神经网络的非线性预测的工作特性决定了其工作范围的广泛性——现有的工作预测内容是材料的疲劳-蠕变寿命,在以后的预测工作中利用BP神经网络还可以预测如热疲劳寿命等本构更为复杂的预测类型;相反的,在知道材料的疲劳寿命的情况下,可以预测材料的危险最大应力、危险应变幅等。
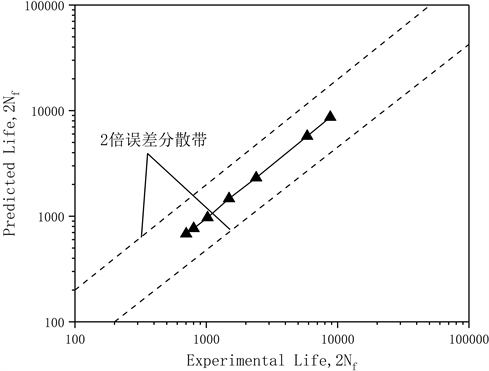
Figure 12. Comparison between the predicted creep fatigue life and the experimental creep fatigue life under different mean stresses and stress amplitudes
图12. 不同平均应力和应力幅值条件下的预测蠕变疲劳寿命与实验蠕变疲劳寿命的比较
结合神经网络的工作特性可得到以下优越性:
1) 没有预测类型限制。在现有阶段的预测模型里,如SWT预测模型,在做预测工作之前均需对已有的数据进行类别划分,如果作用的载荷类型不满足SWT模型的使用要求,则不可以进行预测工作。而BP神经网络预测是基于数据组的非线性预测,只要满足训练组数足够这一要求,即可进行预测工作。因此,BP神经网络的使用限制条件更少,使用范围更广。
2) 可以处理不同类型的问题。同一BP神经网络程序可以处理不同的问题,且结果具有较为较高的准确性。
3) 通过有限的数据可以实现任意参数下的寿命预测。在训练组数据足够多的情况下,对于任意的参数(包括已出现和未出现在训练组的参数)BP神经网络均可以得到相应的预测结果。
3. 结论
通过现有的不同循环条件下的疲劳寿命的实验结果,建立BP神经网络寿命预测模型以预测316L (N)不锈钢的疲劳寿命,同时与现有的Basquin-Coffin-Manson模型、SWT模型和新模型进行预测结果对比,得到的结果表明:BP神经网络模型的预测结果与实验结果吻合良好并且优于三个本构预测模型得到的预测结果,同时BP神经网络模型还成功预测了在非对称应力循环条件下平均应力强化和棘轮效应的竞争机制对疲劳寿命的影响规律;针对现有的疲劳蠕变寿命的实验结果,采用BP神经网络模型能对316L (N)不锈钢的疲劳蠕变寿命进行预测,并得到与实验数据吻合良好的结果。
基金项目
中国工程物理研究院杰出人才专项基金。